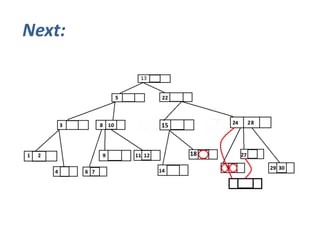
This document discusses 2-4 trees, which are self-balancing data structures where every internal node has either 2, 3, or 4 child nodes. It describes how 2-4 trees allow for efficient searching, insertion, and deletion operations with logarithmic time complexity like other B-tree variants. The document provides examples of how nodes are split or merged during insertion or deletion to maintain the structure's balance properties, ensuring the tree remains of height O(log n).

2. DATA STRUCTURE
17/01/2015
OHIDA ISLAM
2-4 TREE

3. Tree
• A tree is a data structure made up of nodes
or vertices and edges without having any
cycle.
• It also can be defined recursively Tree is
collection of nodes.
• When this tree will have no nodes that is
called NULL or empty tree.

5. 2-4 TREE
• A 2–4 tree is a self-balancing data structure.
• The numbers mean a tree where
every node with children has either two,
three, or four child nodes.
• All leaf nodes are at the same level And All
external nodes have the same depth.
• High of 2-4 tree is at least log4 and at most
log2
• Each node can store 1,2 or 3 entries

6. 2 Node
A 2-node has
one data
element, and
internal has
two child
nodes.
a

7. 3 Node
A 3-node has
two data
elements,
and internal
has three
child nodes.
a b

8. 4 Node
A 4-node has
three data
elements,
and if
internal has
four child
nodes.
ab c
p
Q R
S

9. 2-4 TREE
22
5 10 25
3 4 6 8 14 23 24 27
11 13 17

10. 2–4 trees are B-trees of order
4. Like B-trees in general, they
can search, insert and delete.
So now I am going to show
how can search from 2-4 tree.

11. SEARCHING
50
30 70
20 35 40 60 80
15 25 32 37 45 55 65 75 85

12. INSERTION
:
21,23,40,41,7
No problem if the node
has
empty tree

13. INSERT 21:

14. Insert 23:

15. Insert 40:

16. Insert 41:

17. Nodes get split if there is insufficient
space:

18. NEXT:

19. If parents node does not have sufficient space then
it is split . In this manner splits can cascade.

20. NEXT:

21. DELETION:

22. DELETE 21:

23. IF KEY TO BE DELETED IS AN INTERNAL NODE THEN WE
SWAP IT WITH ITS PREDECESSOR AND THEN DELETE IT.

24. NEXT:

25. If after deleting a key a node becomes empty then we
borrow a key from its sibling:

26. EMPTY NODE:

27. Next:

28. After delete:

29. If siblings has only one key then we merge with it. The key in
the parent node separating these two siblings moves down
into the merged node.

30. Next:

31. NEXT:

32. Conclusion:
 The height of a (2,4) tree is 0(log n)
 Split, transfer and merge each take
0(1).
 Search, insertion and deletion each
take 0 (log n).