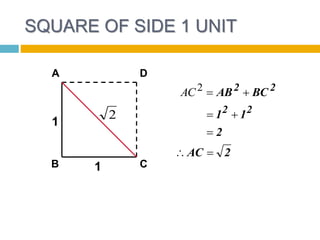
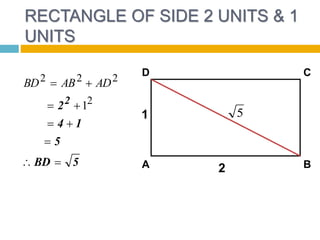
This document discusses irrational numbers, which are numbers that cannot be expressed as a ratio of two integers, such as the square root of 2. It provides examples of irrational numbers that arise from calculations involving the sides of geometric shapes, such as the square root of 2 being the length of the diagonal of a unit square. The document also covers operations involving irrational numbers, stating that the product and quotient of irrational numbers are irrational numbers.

1. IRRATIONAL NUMBERS
KALADEVI G.

2. IRRATIONAL NUMBERS
 Numbers which are not rationals are called
irrationals
 Non recurring numbers, non terminating
decimal numbers
Eg:

3. SQUARE OF SIDE 1 UNIT
1
1
2
A D
B C
2AC
2
11
BCAB
22
22



2AC

4. RECTANGLE OF SIDE 2 UNITS & 1
UNITS
D
A B
C
1
2
5
5BD
5
14
22





2
222
1
ADABBD

5. PRODUCT OF IRRATIONALS
 For any two positive numbers x and y,
 Eg.
yxyx 
5353 
636218218 
6.32.13 
525
3
10
2
15
3
10
2
15
3
1
3
2
1
7 

6. DIVISION OF IRRATIONALS
 For any two positive numbers x and y,
 Eg.
y
x
y
x

2
5
2
5

39
3
27
3
27
