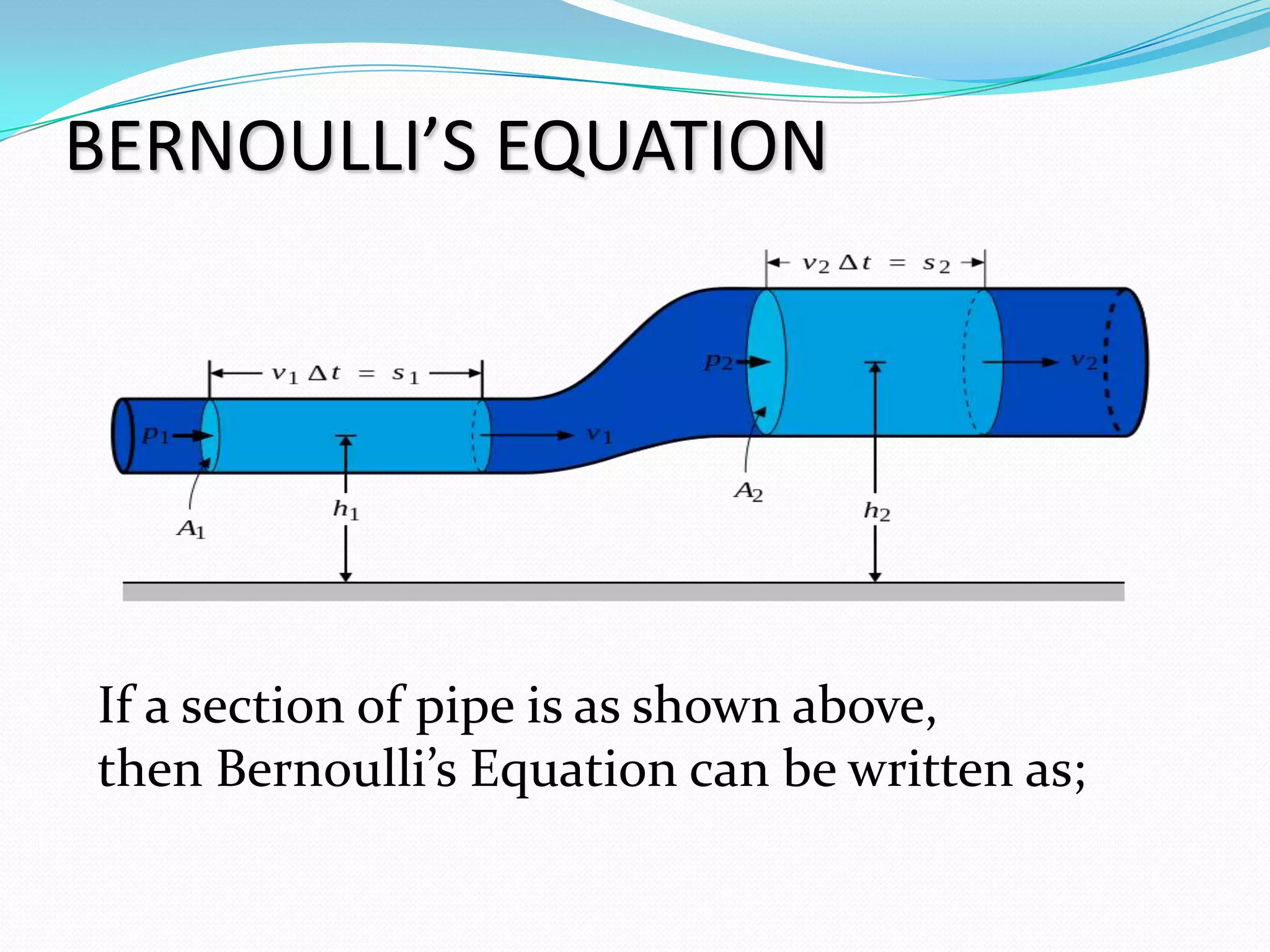
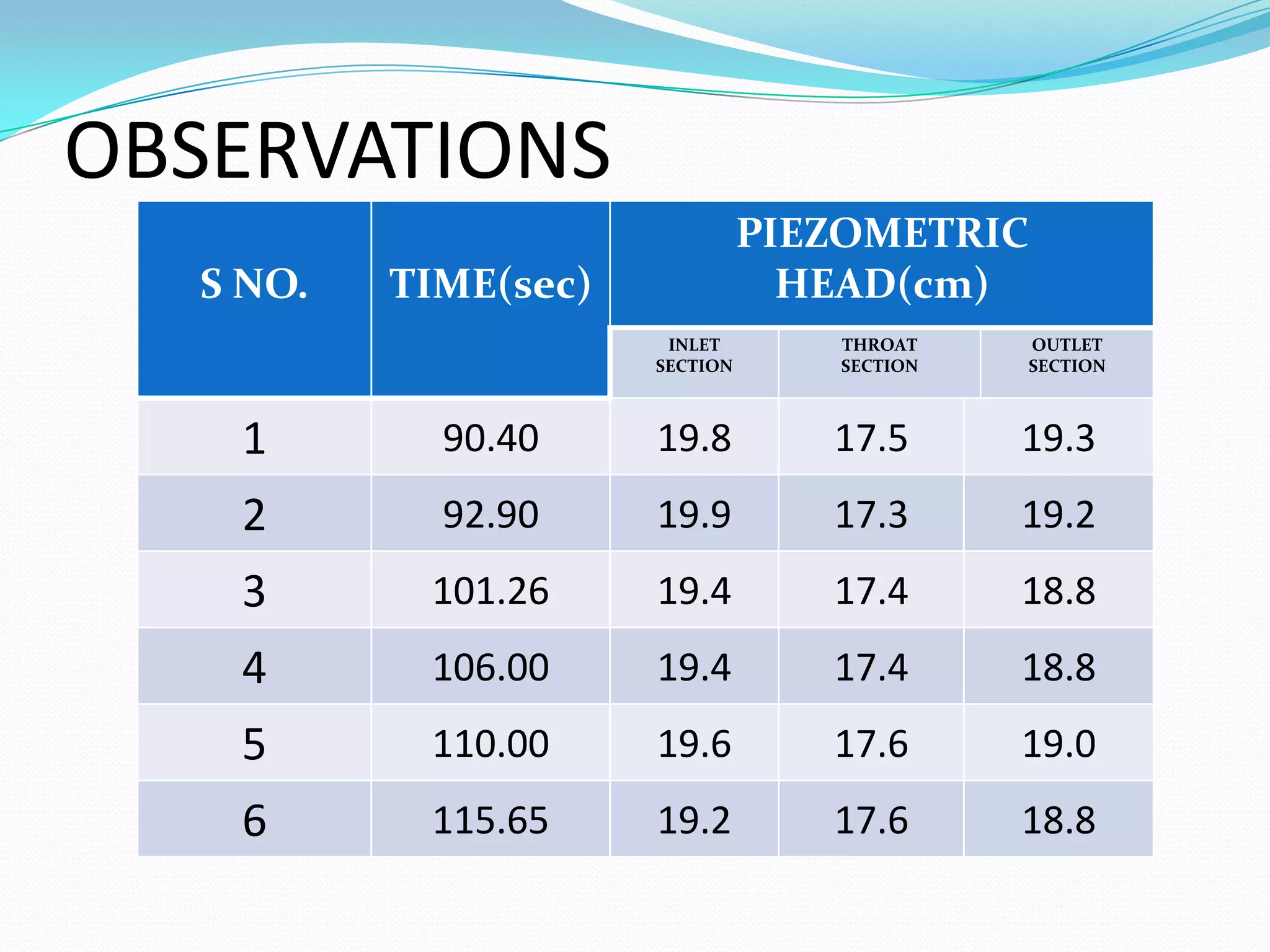
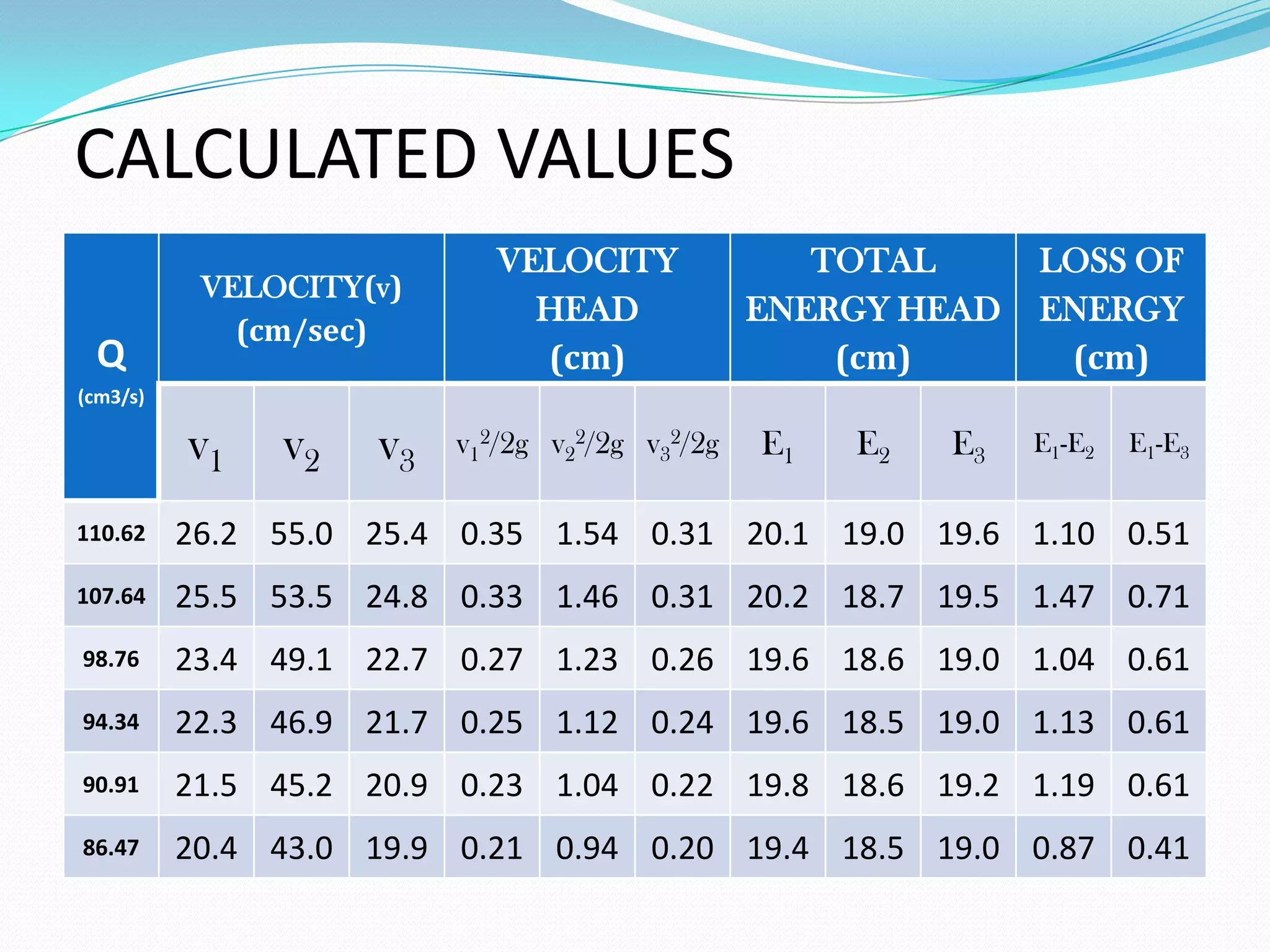
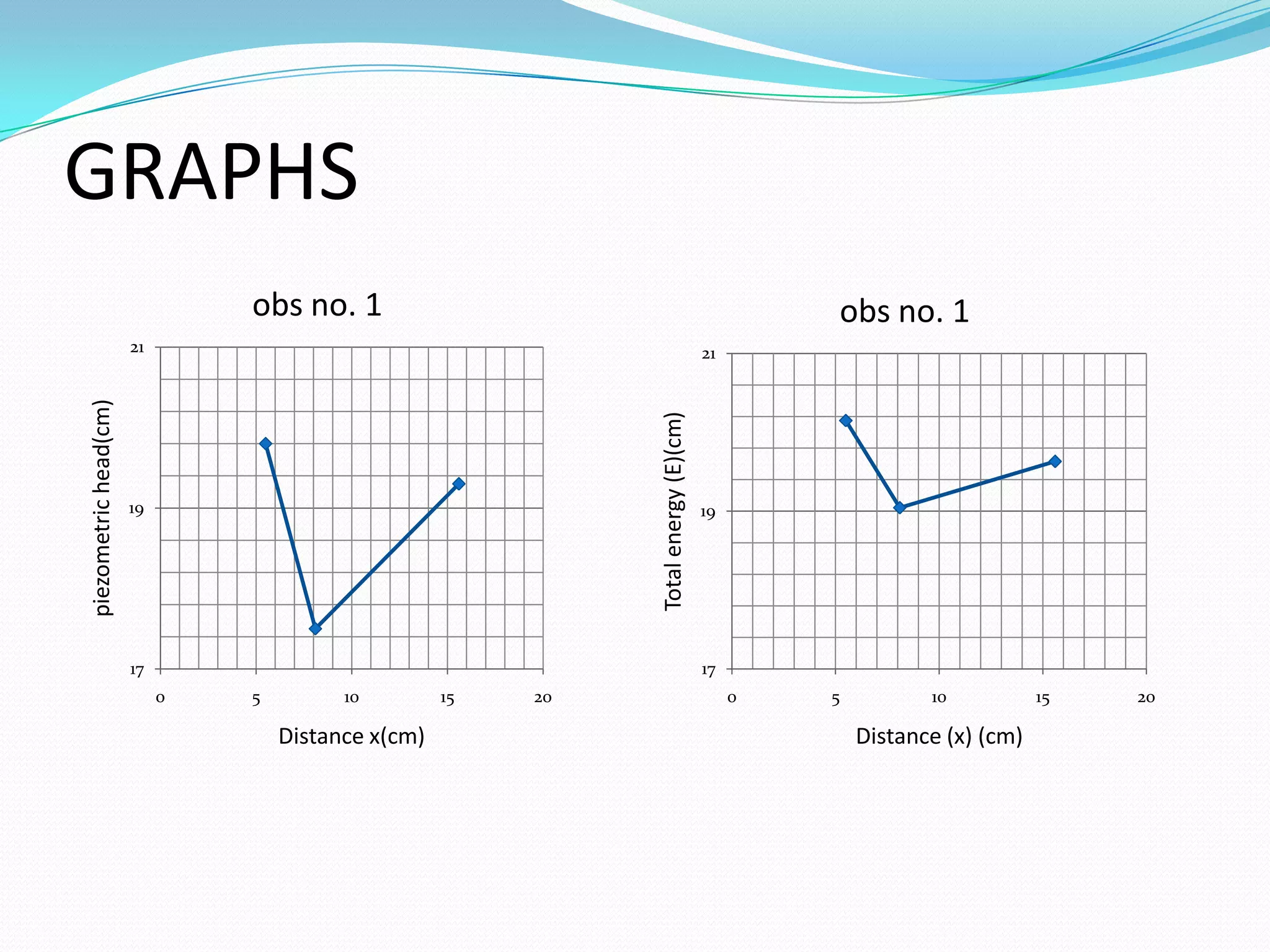
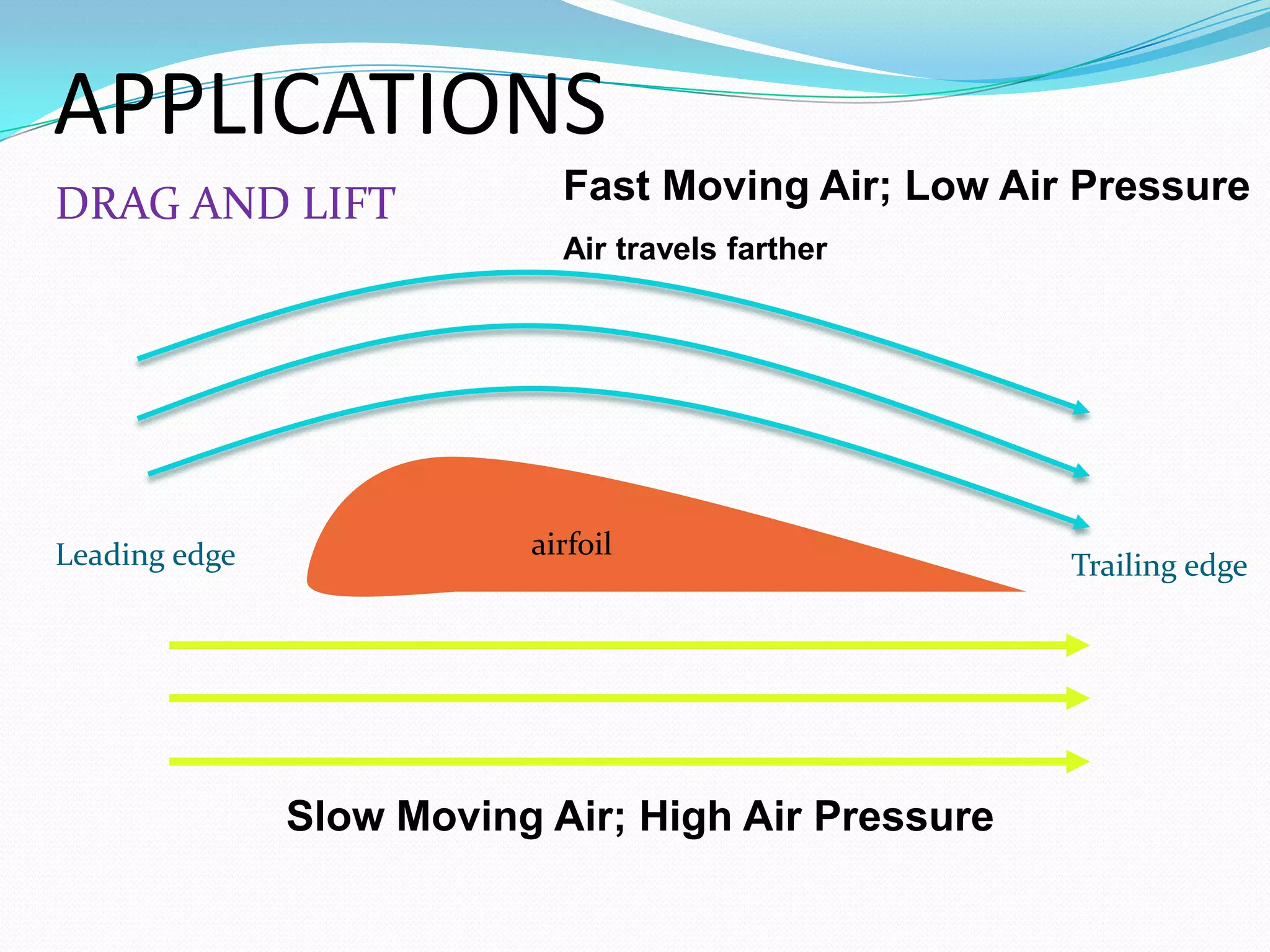
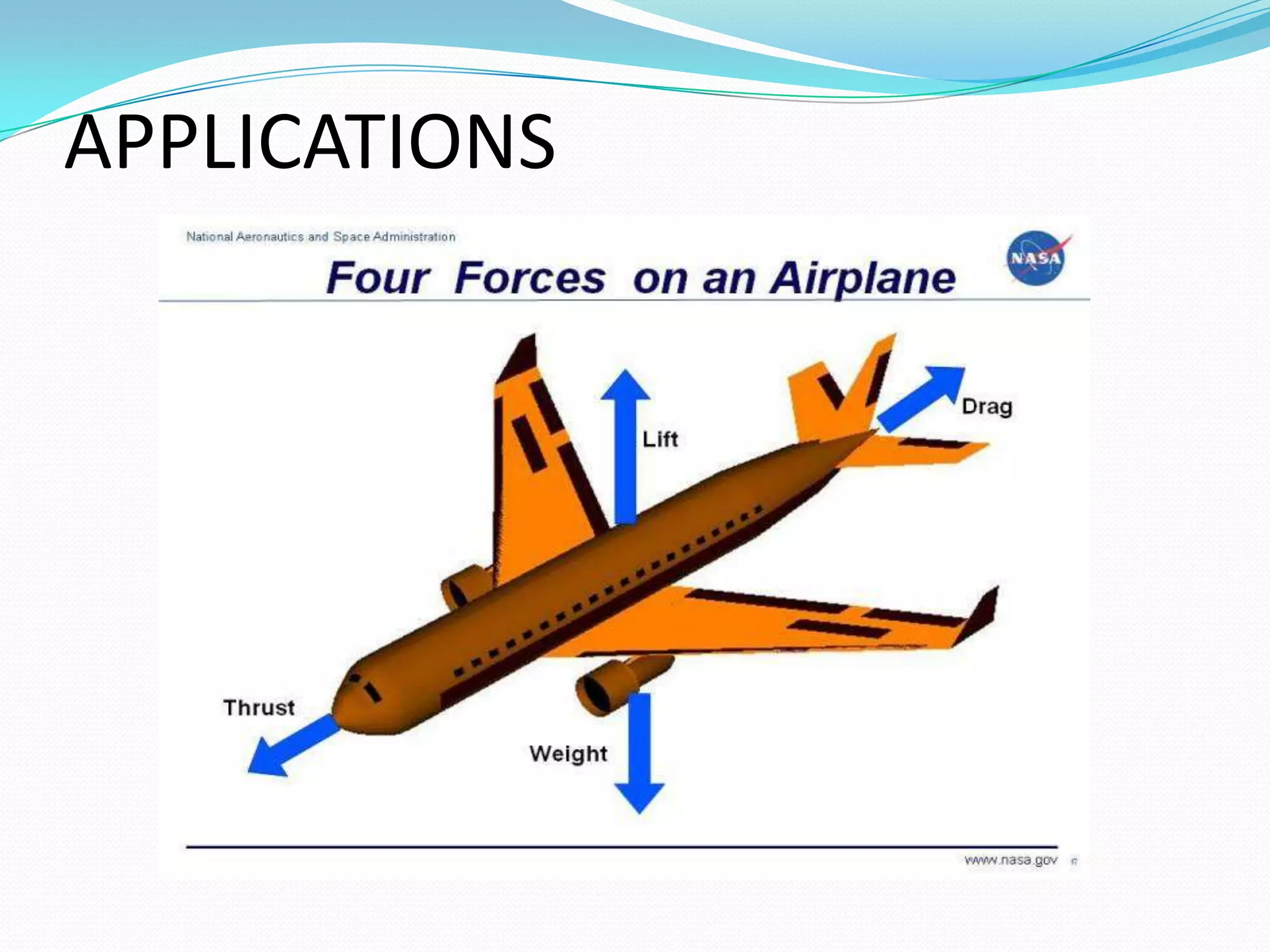
This document summarizes Daniel Bernoulli and his theorem on fluid mechanics. It discusses how Bernoulli, a Swiss scientist born in the 1700s, discovered that an increase in the speed of a moving fluid is accompanied by a decrease in the fluid's pressure. Bernoulli's principle, also called Bernoulli's theorem, states that the total energy in a fluid remains constant provided the flow is steady, frictionless, and incompressible. The document then provides Bernoulli's equation and describes experiments using a Venturi meter to verify the theorem by measuring pressure and velocity changes at different pipe sections. It concludes that the experiments validate Bernoulli's equation and its applications in fluid mechanics and aerodynamics.

1. S M Mozakkir Quadri
10CES-54(5th SEM)
JAMIA MILLIA ISLAMIA

2. INDRODUCTION
Daniel Bernoulli
A Swiss scientist born in
1700’s that is most famous
for his work in fluid
pressure. He died in 1782.

3. BERNOULLI’S THEOREM
Bernoulli’s theorem which is also known as
Bernoulli’s principle, states that an increase in the
speed of moving air or a flowing fluid is
accompanied by a decrease in the air or
fluid’s pressure or sum of the kinetic (velocity
head), pressure(static head) and Potential energy
energy of the fluid at any point remains constant,
provided that the flow is steady, irrotational, and
frictionless and the fluid is incompressible.

4. BERNOULLI’S EQUATION
If a section of pipe is as shown above,
then Bernoulli’s Equation can be written as;

5. BERNOULLI’S EQUATION
Where (in SI units)
P= static pressure of fluid at the cross section;
ρ= density of the flowing fluid in;
g= acceleration due to gravity;
v= mean velocity of fluid flow at the cross section in;
h= elevation head of the center of the cross section with
respect to a datum.

6. HOW TO VERIFY?
The converging-diverging nozzle apparatus (Venturi
meter) is used to show the validity of Bernoulli’s
Equation. The data taken will show the presence of fluid
energy losses, often attributed to friction and the
turbulence and eddy currents associated with a
separation of flow from the conduit walls.

7. APPARATUSES USED
 Arrangement of Venturi
meter apparatus(fig.1)
 Hydraulic bench(fig. 2).
 Stop watch(fig.3).
fig. 2 fig. 3

8. PROCEDURE
1. Note down the inlet, throat and outlet section areas.
2. Measure the distances of inlet, throat ant outlet
section from origin.
3. Switch on the motor attached to hydraulic bench.
4. If there any water bubble is present in tube remove it
by using air bleed screw.
5. Fully open the control valve.
6. Note down the reading of piezometer corresponding
to the section, simultaneously note down the time
required to a constant rise of water in volumetric
tank(say of 10).
7. Varying the discharge and take at least six readings.

9. OBSERVATIONS
1. Volume = 1000 cm3
2.Distance of inlet section from origin= 5.5 cm
3. Distance of throat section from origin= 8.1 cm
4.Distance of outlet section from origin= 15.6 cm
5.Area of inlet section= 4.22 cm2
6.Area of throat section= 2.01 cm2
7.Area of outlet section= 4.34 cm2

10. OBSERVATIONS
PIEZOMETRIC
S NO. TIME(sec) HEAD(cm)
INLET THROAT OUTLET
SECTION SECTION SECTION
1 90.40 19.8 17.5 19.3
2 92.90 19.9 17.3 19.2
3 101.26 19.4 17.4 18.8
4 106.00 19.4 17.4 18.8
5 110.00 19.6 17.6 19.0
6 115.65 19.2 17.6 18.8

11. CALCULATED VALUES
VELOCITY TOTAL LOSS OF
VELOCITY(v)
HEAD ENERGY HEAD ENERGY
(cm/sec)
Q (cm) (cm) (cm)
(cm3/s)
v1 v2 v3 v12/2g v22/2g v32/2g E1 E2 E3 E1-E2 E1-E3
110.62 26.2 55.0 25.4 0.35 1.54 0.31 20.1 19.0 19.6 1.10 0.51
107.64 25.5 53.5 24.8 0.33 1.46 0.31 20.2 18.7 19.5 1.47 0.71
98.76 23.4 49.1 22.7 0.27 1.23 0.26 19.6 18.6 19.0 1.04 0.61
94.34 22.3 46.9 21.7 0.25 1.12 0.24 19.6 18.5 19.0 1.13 0.61
90.91 21.5 45.2 20.9 0.23 1.04 0.22 19.8 18.6 19.2 1.19 0.61
86.47 20.4 43.0 19.9 0.21 0.94 0.20 19.4 18.5 19.0 0.87 0.41

12. RESULTS
It is observed from the calculated value that at section
where area is less velocity is high and pressure is low
which validates the Bernoulli’s Equation. Graphs are
plotted between distance v/s piezometric head and
distance v/s total energy but from the graph (B) we can
observe that there is dissipation in energy at last point
this is because to achieve an ideal condition practically is
not possible.

13. GRAPHS
obs no. 1 obs no. 1
21 21
piezometric head(cm)
Total energy (E)(cm)
19 19
17 17
0 5 10 15 20 0 5 10 15 20
Distance x(cm) Distance (x) (cm)

14. APPLICATIONS
The Bernoulli’s equation forms the basis for solving a
wide variety of fluid flow problems such as jets issuing
from an orifice, jet trajectory flow under a gate and over
a weir, flow metering by obstruction meters, flow
around submerged objects, flows associated with pumps
and turbines etc.
Apart from this Bernoulli’s equation is very useful in
demonstration of various aerodynamic properties like
Drag and Lift.

15. APPLICATIONS
DRAG AND LIFT Fast Moving Air; Low Air Pressure
Air travels farther
Leading edge airfoil
Trailing edge
Slow Moving Air; High Air Pressure

16. APPLICATIONS

17. CONCLUSION
From the result obtained, we can
conclude that the Bernoulli’s equation is
valid for flow as it obeys the equation. As
the area decreases at a section (throat
section) velocity increases, and the
pressure decreases.

18. THANK YOU