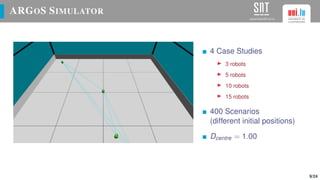
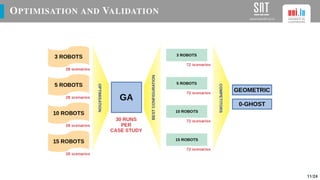
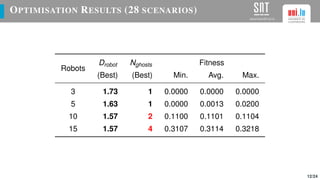
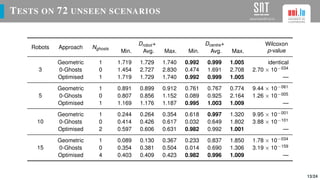
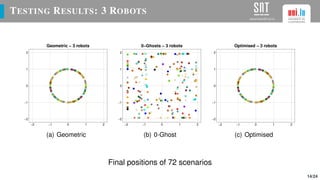
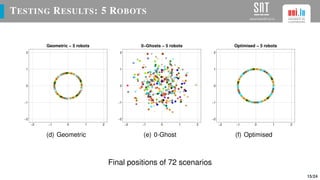
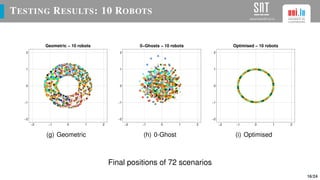
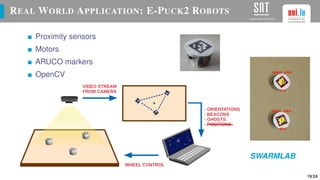
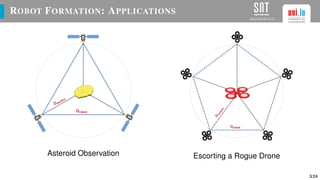
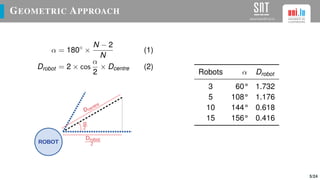
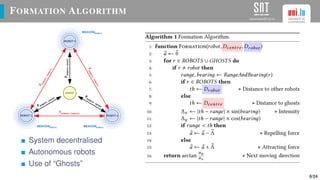
The document presents a study on optimizing parameters for autonomous robot swarm formations using a genetic algorithm (GA). It details the approaches taken, experimental results, and validation of the proposed algorithms through testing with real robots, achieving stable formations under various scenarios. Future work includes expanding robot numbers and developing a 3D formation model.

1. University of Luxembourg
Multilingual. Personalized. Connected.
Optimising Autonomous Robot Swarm Parameters for Stable Formation Design
Daniel H. Stolfi1
Grégoire Danoy1,2
The Genetic and Evolutionary Computation Conference – GECCO 2022
July 9th – 13th, 2022
1
SnT - Interdisciplinary Centre for Security, Reliability and Trust, University of Luxembourg, Luxembourg
2
FSTM/DCS, University of Luxembourg, Luxembourg

2. TABLE OF CONTENTS
1 INTRODUCTION
2 ROBOT FORMATION APPROACHES
3 EXPERIMENTAL RESULTS
4 CONCLUSIONS AND FUTURE WORK

3. TABLE OF CONTENTS
1 INTRODUCTION
2 ROBOT FORMATION APPROACHES
3 EXPERIMENTAL RESULTS
4 CONCLUSIONS AND FUTURE WORK
1/24

4. ROBOT FORMATION
Coordination of swarms of robots
Predefined shapes
Self Organisation
Collective tasks:
I Surveillance
I Salvage
I Mapping
I Displays
I Etc. Image source: https://newsroom.intel.com/
2/24

5. ROBOT FORMATION: APPLICATIONS
Asteroid Observation Escorting a Rogue Drone
3/24

6. TABLE OF CONTENTS
1 INTRODUCTION
2 ROBOT FORMATION APPROACHES
3 EXPERIMENTAL RESULTS
4 CONCLUSIONS AND FUTURE WORK
4/24

7. GEOMETRIC APPROACH
α = 180◦
×
N − 2
N
(1)
Drobot = 2 × cos
α
2
× Dcentre (2)
Robots α Drobot
3 60° 1.732
5 108° 1.176
10 144° 0.618
15 156° 0.416
5/24

8. FORMATION ALGORITHM
System decentralised
Autonomous robots
Use of “Ghosts”
6/24

9. OPTIMISATION ALGORITHM
Genetic Algorithm (GA)
Operators:
I Binary tournament
I Single Point Crossover (Pc = 0.9)
I Integer Polynomial Mutation (Pm = 1
L
)
I Best individual in offspring replaces the worst individual in population
Problem representation: ~
x = {Drobot , Nghosts}
Problem constraints:
I DGeometric ≤ Drobot ≤ 4 × DGeometric
I 1 ≤ Nghosts ≤ 4
7/24

10. EVALUATION: FITNESS FUNCTION
F(~
x) =
1
M
M
X
j
[P(~
x) + min(~
x) + max (~
x)] + ω(G − 1) (3)
P(~
x) = k
N
X
i
~
rik (4)
εmin(~
x) =
N
X
i
| min[D(~
ri, ~
centre)] − Dcentre| (5)
εmax (~
x) =
N
X
i
| max[D(~
ri, ~
centre)] − Dcentre| (6)
8/24

11. ARGOS SIMULATOR
4 Case Studies
I 3 robots
I 5 robots
I 10 robots
I 15 robots
400 Scenarios
(different initial positions)
Dcentre = 1.00
9/24

12. TABLE OF CONTENTS
1 INTRODUCTION
2 ROBOT FORMATION APPROACHES
3 EXPERIMENTAL RESULTS
4 CONCLUSIONS AND FUTURE WORK
10/24

13. OPTIMISATION AND VALIDATION
11/24

14. OPTIMISATION RESULTS (28 SCENARIOS)
Robots
Drobot Nghosts Fitness
(Best) (Best) Min. Avg. Max.
3 1.73 1 0.0000 0.0000 0.0000
5 1.63 1 0.0000 0.0013 0.0200
10 1.57 2 0.1100 0.1101 0.1104
15 1.57 4 0.3107 0.3114 0.3218
12/24

15. TESTS ON 72 UNSEEN SCENARIOS
Robots Approach Nghosts
Drobot ? Dcentre? Wilcoxon
p-value
Min. Avg. Max. Min. Avg. Max.
3
Geometric 1 1.719 1.729 1.740 0.992 0.999 1.005 identical
0-Ghosts 0 1.454 2.727 2.830 0.474 1.691 2.708 2.70 × 10−034
Optimised 1 1.719 1.729 1.740 0.992 0.999 1.005 —
5
Geometric 1 0.891 0.899 0.912 0.761 0.767 0.774 9.44 × 10−061
0-Ghosts 0 0.807 0.856 1.152 0.089 0.925 2.164 1.26 × 10−005
Optimised 1 1.169 1.176 1.187 0.995 1.003 1.009 —
10
Geometric 1 0.244 0.264 0.354 0.618 0.997 1.320 9.95 × 10−001
0-Ghosts 0 0.414 0.426 0.617 0.032 0.649 1.802 3.88 × 10−101
Optimised 2 0.597 0.606 0.631 0.982 0.992 1.001 —
15
Geometric 1 0.089 0.130 0.367 0.233 0.837 1.850 1.78 × 10−034
0-Ghosts 0 0.354 0.381 0.504 0.014 0.690 1.306 3.19 × 10−159
Optimised 4 0.403 0.409 0.423 0.982 0.996 1.009 —
13/24

16. TESTING RESULTS: 3 ROBOTS
(a) Geometric (b) 0-Ghost (c) Optimised
Final positions of 72 scenarios
14/24

17. TESTING RESULTS: 5 ROBOTS
(d) Geometric (e) 0-Ghost (f) Optimised
Final positions of 72 scenarios
15/24

18. TESTING RESULTS: 10 ROBOTS
(g) Geometric (h) 0-Ghost (i) Optimised
Final positions of 72 scenarios
16/24

19. TESTING RESULTS: 15 ROBOTS
(j) Geometric (k) 0-Ghost (l) Optimised
Final positions of 72 scenarios
17/24

20. TESTING RESULTS: ARGOS
18/24

21. REAL WORLD APPLICATION: E-PUCK2 ROBOTS
Proximity sensors
Motors
ARUCO markers
OpenCV
SWARMLAB
19/24

22. E-PUCK2 FORMATION
20/24

23. TABLE OF CONTENTS
1 INTRODUCTION
2 ROBOT FORMATION APPROACHES
3 EXPERIMENTAL RESULTS
4 CONCLUSIONS AND FUTURE WORK
21/24

24. CONCLUSIONS
We have proposed a new formation algorithm
We have optimised its parameters using a GA
Several ghosts were needed in the more complex scenarios
Our approach have achieved stable formations in the 288 unseen scenarios
We have also validated our proposal using real robots (E-Puck2)
22/24

25. FUTURE WORK
More robots
3-D formation model
23/24

26. QUESTIONS?
Daniel H. Stolfi
daniel.stolfi@uni.lu
https://adars.uni.lu/
https://pcog.uni.lu/
https://wwwen.uni.lu/snt/
https://wwwen.uni.lu/
Optimising Autonomous Robot Swarm Parameters for Stable Formation Design
Daniel H. Stolfi1, and Grégoire Danoy1,2
1 SnT - Interdisciplinary Centre for Security, Reliability and Trust, University of Luxembourg, Luxembourg
2 FSTM/DCS, University of Luxembourg, Luxembourg
This work is supported by the Luxembourg National Research Fund (FNR) – ADARS Project, ref. C20/IS/14762457. The experiments presented in this paper
were carried out using the the SwarmLab facility of the FSTM/DCS and the HPC facilities of the University of Luxembourg – see https://hpc.uni.lu.
24/24