Thinking and working mathematically

Thinking and Working Mathematically Loddon Mallee 2010

Numeracy is the capacity, confidence and disposition to understand and apply mathematical concepts, problem solve, collect and analyse data and to make connections within mathematics to meet the demands of learning at school, work, home, community and within civic life. Literacy and Numeracy Statement Blueprint Implementation Paper DEECD 2009 Numeracy

Common Numeracy Situations in Everyday Life. Activity A look at some time in a normal day eg: List the mathematical decisions you made from the time you woke up this morning until about 9.30? eg: List the mathematical decisions you might be making while in a car on the way to work or school this morning eg: List mathematical decisions you made in your lunch hour An activity for maths coordinators for professional learning for teachers; and an activity to use with students

This module: Explicit Instruction: Thinking and Working Mathematically using the Multi- Modal Think Board Differentiation using the Multi- Modal Think Board Using questions to differentiate tasks within mathematical modes An Instruction Model with differentiation in mind

Differentiating by: Asking frequent, targeted, rigorous questions of students as they demonstrate mastery Planning ,working, assessing and reflecting in different mathematical modes Working in different ways within a given mode Using tasks that are open question based

The Mathematical Modes [The Singapore Multi-modal Think Board]

Thinking/Working Mathematically: A Think-Board [Multi-Model] to Teach Mathematics Using Multi-Modal Think-Board to Teach Mathematics Khoon Yoong Wong, Mathematics and Education Academic Group , National Institute of Education, Nanyang Technological University, Singapore, July 2004 e 5 Number- calculate e 5 Word- communicate e 5 Diagram- visualise e 5 Symbol- manipulate [algebra] e 5 Real Thing- do [eg: manipulative materials] e 5 Story- apply Thinking/Working Mathematically

Group Work in Mathematics : Whole group- small group – whole group Pairs is the most effective way to work in groups in mathematical contexts. (Students also need to be given the opportunity to work individually and practise being able to work individually).

Using the Multi-Modal Think Board Topic - Measurement and Subtraction Real Thing – do [Level 1- 5] What might students ‘do’ [action] to calculate the difference in height between 2 people? Real Thing – do [Level 5-6] For two ladders - ladder [a] 410cm in length and ladder [b] 420cm in length Ladders [a] and [b] are leaning against a wall. They touch the wall 400cm above the ground. What is the difference in the distance between the foot of each of the ladders and the wall?

Working/Thinking Mathematically Using Multi-modal Think Boards Khoon Yoong Wong 2004 Real Thing- Do the use of concrete manipulatives principle- learning by doing : I hear I forget; I see and I remember; I do and I understand [Piaget,Bruner] grounding mathematical ideas in concrete situations helps develop mental models that provide meaning to abstract symbols , hence reducing the chance of anxiety phobia towards mathematics without sufficient practical experience students have been found to lack numerical sense of measures about real objects and hence cannot determine whether their answers are reasonable or not in the real world

Working/Thinking Mathematically Using Multi-modal Think Boards Khoon Yoong Wong 2004 Real Thing- Do [continued] the transition from practical activities to formal abstraction, however, is not easy [Johnson 1989] poorly designed manipulatives or improper use can hinder rather than facilitate conceptual development ‘ virtual manipulative’ – electronic technologies to support effective mathematics teaching

Using the Multi-Modal Think Board * [ Level 2- 4] Calculate the difference in number, between two groups of objects. One group of 39 and the other 17. * [Level 3- 5] Calculate the difference between 2.48m and 11.48 m Symbol – manipulate whole - part concept comparison [ compare collections when one collection is larger than another and with like and unlike objects] change concepts [ increase or increment problems and decrease or deficit problems] manipulate the equation [‘milk the equation for all it’s worth’] Story – apply Write problem s with an authentic context using the equations that result

Using the Multi-Modal Think Board Symbol Mode- manipulate Real - apply * 12 + 5 = 17 * 17 + 39 = 56 7 x 6 = 42 *480 ÷ 20 = 24 1. Rewrite the equations in as many ways as you can using only the numbers [values] provided. One of the numbers needs to be represented as an ‘unknown’ [variable] in each equation you write. 2. Write word problems (which have an authentic context) for some of the equations

The Change Concept Try these for example – and there are more : 39 + 17 = ( increase, result unknown) 17 + = 56 ( increase, change unknown) + 17 = 56 ( increase, start unknown) 56 - 17 = = ( decrease, result unknown) - 39 = 17 ( decrease, start unknown) 17 39 ? 17 ? 56 f 56 17 ? 56 17 ? ? 39 17

Using the Multi-Modal Think Board Topic - Measurement and Division 86 220m of rope was divided into 6 equal lengths to be sold. How much rope was in each of the lengths? If 2/3 of the rope lengths were damaged in a fire how many metres of rope were not damaged? Symbolic – manipulate Syntactic - what do I need to know to work this out with a calculator?; division operation; fraction as an operator… Diagram - visualise- How might we demonstrate this problem in a diagram?

Using the Multi-Modal Think Board Khoon Yoong Wong 2004 Diagram- Visualise Key word: represent pictures diagrams graphs charts figures illustrations come in varying degrees of abstraction eg: a picture of several apples versus several dots can be a pictorial summary of work done in ‘real thing ‘ mode visual imagery ‘in the mind’s eye’

Using the Multi-Modal Think Board Topic – Division of fractions 6 ÷ ½ = 6 ½ ¼ Diagram – visualise Story - application =

Using the Multi-Modal Think Board Topic – Fractions One hundred and eighty people attended a school function. If 1/3 of them were students how many people were not students? Number- Calculate Essential basic skills Processes Algorithms ‘ working out’ Strategies Diagram - visualise 180 60 60 60 1/3 180 people 1/3 students 180 ÷ 3 = 60 One third = 60

Using Multi-Modal Think Boards Khoon Yoong Wong 2004 Word – Communication words are essential for communicating mathematical ideas and thinking about them as a mode of representation, it also includes phrases and sentences as students often confuse the meaning of the same work when used in everyday situations and in mathematics more acute when students learn mathematics in a foreign language teachers should say mathematical terms precisely and consistently eg: x ² is ‘x to the power of 2’ and not ‘x two’

Thinking and working mathematically 6 modes for thinking and working mathematically Instruction in all modes regularly, consistently- ie: where appropriate Explicit instruction using closed questions Tasks design - using open questions Differentiation though using open questions

Using the Multi-Modal Think Board Topic- multiplication [Level 4 - 5] A closed question Peter planted tomatoes seedlings in 35 rows with 20 in each row. If each plant produced [an average of] 43 tomatoes, what was the total crop? Pairs/draw/discuss In what ways might you represent this problem using a ‘diagram’ ? Opening up the question/task If Peter planted 375 tomatoes in rows and each plant produced 43 [on average] tomatoes, what might the planting in the rows look like? How many tomatoes did he have to sell? If students were asked to represent this problem using manipulative materials/contexts what might that involve?

del 45 x 25 = 4 5 2 5 x 800 200 25 100 x 4 5 2 5 800 100 200 25 1 125 [40x20]+[40x5]+[5x5]+[5x20]=1 125 900 225 2 3 x 3 4 0 9 1 6 0 2 8 1 0 2 8 1 7 Lattice method Differentiation- calculate in different ways

Using the Multi-Modal Think Board Topic- [might be?] A closed task [ Level 5] Round off 1.29 to the nearest tenth In what ways might you represent this problem using a ‘diagram’ ? Pairs/draw/discuss Opening up the question/task [ Level 5] What numbers when rounded off become 1.3? What modes could you ask students to use to model / demonstrate understanding here?

del Using the Multi-Modal Think Board Topic – [might be ?] Closed context/task [Level 5] 0.7 x 5 = Open task could be: [Level 5] The product of two numbers is 3.5. What might be the two numbers be? Pairs - What are activities you could ask students to do in each of the modes for this problem? Diagram - visualise Number - calculate Story - apply Real Thing - do Symbol - manipulate Word - communicate

del Using a Multi- Modal Think Board Topic – [might be ?] Closed context/task [Level 6] Circle the number which is closest to 5.4 5.3 5.364 5.46 5 5.6 5.453 Open task Word – communicate One of your friends ask you to explain the best way to decide which number is closest to 5.4. How would you explain how to work out which number is closest to 5.4?

Using the Multi – Modal Think Board Content specific mathematics through questions/tasks Which fraction is smaller? A corresponding open question/task is : Level 5 What are some fractions smaller than Discuss – in pairs, work through the 6 modes. How might this task be addressed using each of the modes? Discuss Peter Sullivan 2003 3 4 4 5 or 4 5 ?

[Level 5.6] Open task Progressively remove numbers replacing them with blanks gets us to a task like this Addition of Fractions Closed question 1 7 3 4 + = 1 ? ? + = ? ? ? 12

A Balanced Mathematical Program Charles Lovitt A balanced mathematics program: Will meet individual needs of students AND Ensure students are working mathematically What do we mean by ‘working mathematically’? [Turn and talk]

A Balanced Mathematics Program Charles Lovitt Working mathematically simultaneously involves: essential skills practice AND ( of equal importance) thinking, reasoning and communication (Dimension of Structure) AND meeting the demand of huge mixed ability in any given group- [potentially a 7 year spread in any class]

Using the Multi - Modal Think Board Division of a decimal by an integer 0 . 4 ÷ 2 = [zero point four divided by two] Task [a] and [c] – most students no difficulty Task [d] to [f] – more difficult When the task is changed to 0.4 ÷ 0.2 = even [a] and [b] become difficult and most students would not be able to complete Using Multi-Modal Think-Board to Teach Mathematics Khoon Yoong Wong [a] Read this aloud - word [b] calculate its value [not with a calculator] - number [c] draw a diagram to illustrate the operation - diagram [d] demonstrate the operation using real objects - real thing [e] write a story or word problem that can be solved using this operation – story [f] extend this operation to algebra – symbol - symbol

Think- Board Use for: planning instruction reflection assessment

An Instruction Model [one of many…] Andrew Fuller- The Get It! Model http://www.lccs.org.sg/downloads/10Creating_Resilient.pdf Link

‘ We’re sometimes socialised to think we have to break students up into different instructional groups to differentiate, giving them different activities and simultaneously forcing ourselves to manage an overwhelming amount of complexity.’ Doug Lemnov, Teach like a Champion 2010

‘ Asking frequent, targeted, rigorous questions of students as they demonstrate mastery, is a powerful and much more effective tool for differentiating’ Ask how or why. Ask for another answer. Ask for a better word. Ask for evidence. Ask students to integrate a related skill. Ask students to apply the same skill in a new setting. Doug Lemnov, Teach like a Champion 2010

Creating Resilient Learners- The Get It! Model of Learning 2003 Andrew Fuller 5 mins Maximum10 minutes 10-15 mins 10 mins 10- 15 minutes 5 mins Approximate Times [arbitrary] Instruction Model for Long Term Memory Input- Andrew Fuller

Andrew Fuller Creating Resilient Learners- The Get It! Model of Learning 2003 ‘ Window of Opportunity’- Long Term Memory 5 mins Maximum10 minutes 10-15 mins 10 mins 10- 15 minutes 5 mins Ritual Tying it together . Trying out new behaviours – new knowledge and understanding 2 nd Memory Peak Instruction Model- Andrew Fuller Suggested/arbitrary Further exploration of new knowledge and understanding

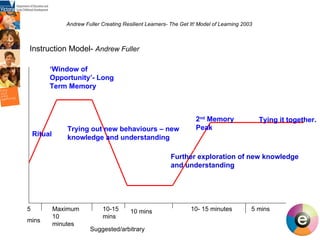
Creating Resilient Learners- The Get It! Model of Learning 2003 Andrew Fuller 5 mins Maximum10 minutes 10-15 mins 10 mins 10- 15 minutes 5 mins Approximate Times [arbitrary] Instruction Model for Long Term Memory Input- Andrew Fuller Closed Question [s] Modelling/Explicit teaching Open question [to differentiate a task] Exploration of the task Whole Group discussion Target Group Skills practice Demonstrate understanding/new knowledge ‘another way’ and or a new open question around the key understanding for the session Whole Group- reflection

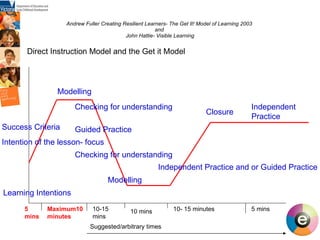
Andrew Fuller Creating Resilient Learners- The Get It! Model of Learning 2003 5 mins Maximum10 minutes 10-15 mins 10 mins. 10- 15 minutes 5 mins Whole group Small groups [pairs/individual] Whole group Small group [target] Small groups- pairs/individual and Independent -Skills Practice Whole Group Whole Group/Small Group Modelled, Shared, Guided Mathematics Suggested/arbitrary times

Andrew Fuller Creating Resilient Learners- The Get It! Model of Learning 2003 and John Hattie- Visible Learning 5 mins Maximum10 minutes 10-15 mins 10 mins 10- 15 minutes 5 mins Learning Intentions Modelling Intention of the lesson- focus Success Criteria Checking for understanding Guided Practice Modelling Checking for understanding Closure Independent Practice and or Guided Practice Independent Practice Direct Instruction Model and the Get it Model Suggested/arbitrary times

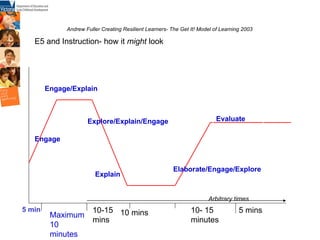
Andrew Fuller Creating Resilient Learners- The Get It! Model of Learning 2003 5 min Maximum10 minutes 10-15 mins 10 mins 10- 15 minutes 5 mins Engage Engage/Explain Explore/Explain/Engage Explain Elaborate/Engage/Explore Evaluate E5 and Instruction- how it might look Arbitrary times

‘ The sequence of learning does not end with a right answer; reward right answers with the follow-up questions that extend knowledge and test for reliability. This technique is particularly important for differentiating instruction’ [Doug Lemnov p41.] closed open ways to write good questions using open questions to differentiate tasks Questions

Peter Sullivan and Pat Lilburn Working backwards Adapt a standard question What are ways to create good questions?

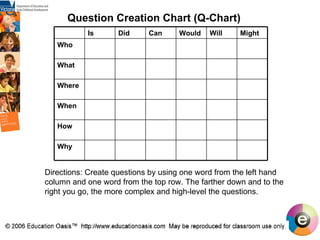
How to Create Good Questions Peter Sullivan/Pat Lilburn Open-ended Maths Activities, Peter Sullivan, Pat Lilburn, Oxford University Press 1997 Method 1: Working Backwards: Step 1 Identify a topic Step 2 Think of a closed question and write down the answer. Step 3 Make up a question which includes [or addresses] the answer eg: Money Total cost $23.50 I bought some items at the supermarket. What might I have bought and what was the cost of each item?

How to Create Good Questions Peter Sullivan/Pat Lilburn Open-ended Maths Activities, Peter Sullivan, Pat Lilburn, Oxford University Press 1997 Method 2: Adapting a standard question: Step 1 Identify a topic Step 2 Think of a standard question Step 3 Adapt it to make a ‘good’ question eg: Subtraction 731-256= Arrange the digits so that the difference is between 100 and 200

The Question Creation Chart- Education Oasis 2006 What are ways to create good questions?

Question Creation Chart (Q-Chart) Directions: Create questions by using one word from the left hand column and one word from the top row. The farther down and to the right you go, the more complex and high-level the questions. Why How When Where What Who Might Will Would Can Did Is

Working/Thinking Mathematically Using Multi-modal Think Boards Khoon Yoong Wong 2004 Story- Apply Linking real world mathematics to ‘text book mathematics reinforces concepts and skills and enhances motivation for learning Story- Apply traditional word problems related to everyday situations reports in the mass media historical accounts of mathematical ideas examples from other disciplines students can and should generate their own

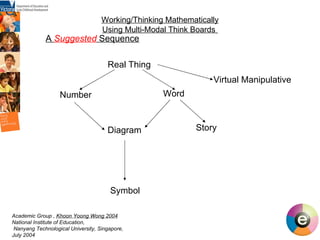
Working/Thinking Mathematically Using Multi-modal Think Boards Khoon Yoong Wong 2004 Using the multi–modal Think Board for Planning, Assessment and Reflection a series of lessons on a particular topic a lesson consider carefully whether all or only some modes will be used in which sequence ie: determine the optimal combination perhaps begin with concrete manipulative materials and support/supplement with virtual [ICT] eg: students may be asked to explain why [a+b]² = a²+ b² using number, diagram and real thing

Working/Thinking Mathematically Using Multi-Modal Think Boards A Suggested Sequence Real Thing Number Word Diagram Symbol Story Virtual Manipulative Academic Group , Khoon Yoong Wong 2004 National Institute of Education, Nanyang Technological University, Singapore, July 2004

Working/Thinking Mathematically Using Think Boards Teachers: For planning – day to day, weekly, units of work For embedding the e 5 For reflection For assessment -encompassing a variety of approaches For…… Students: For reflection For ways of demonstrating understanding/new understanding [elaboration/explanation/reflection…] For problem solving For…….. Turn and talk.

Khoon Yoong Wong, Using Multi-Modal Think-Board to Teach Mathematics Khoon Yoong Wong,Mathematics and Education Academic Group , National Institute of Education, Nanyang Technological University, Singapore, July 2004 -paper Peter Sullivan and Pat Lilburn, Open-ended Maths Activities Oxford University Press 2000 Andrew Fuller Creating Resilient Learners- The Get It! Model of Learning 2003 – Paper John Hattie, Visisble Learning Routledge 2009 George Booker, Denise Bond, Len Sparrow and Paul Swan, Teaching Primary Mathematics 3 rd Edition Pearson Prentice Hall 2004 Doug Lemnov, Teach Like a Champion , Jossey – Bass 2010

Thinking and working mathematically

More Related Content

Similar to Thinking and working mathematically

More from coburgmaths

Recently uploaded

Thinking and working mathematically