Trigonometry 1
•Download as PPT, PDF•
3 likes•1,387 views
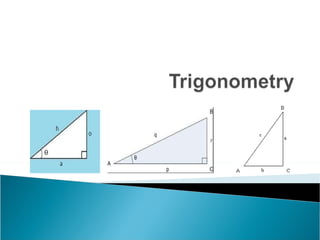
Introduction to sine, cosine and tangent
Report
Share
Report
Share
More Related Content
What's hot
What's hot (20)
Similar to Trigonometry 1
Similar to Trigonometry 1 (20)
Pre-5.1 - trigonometry ratios in right triangle and special right triangles.ppt

Pre-5.1 - trigonometry ratios in right triangle and special right triangles.ppt
Precalculus August 28 trigonometry ratios in right triangle and special righ...

Precalculus August 28 trigonometry ratios in right triangle and special righ...
Trigonometry topic details and table with real example

Trigonometry topic details and table with real example
DEMO-TRIG-FUNCTION-triginometry special angles.pptx

DEMO-TRIG-FUNCTION-triginometry special angles.pptx
Recently uploaded
APM Welcome, APM North West Network Conference, Synergies Across Sectors

APM Welcome, APM North West Network Conference, Synergies Across SectorsAssociation for Project Management
Recently uploaded (20)
Beyond the EU: DORA and NIS 2 Directive's Global Impact

Beyond the EU: DORA and NIS 2 Directive's Global Impact
9548086042 for call girls in Indira Nagar with room service

9548086042 for call girls in Indira Nagar with room service
social pharmacy d-pharm 1st year by Pragati K. Mahajan

social pharmacy d-pharm 1st year by Pragati K. Mahajan
APM Welcome, APM North West Network Conference, Synergies Across Sectors

APM Welcome, APM North West Network Conference, Synergies Across Sectors
Ecosystem Interactions Class Discussion Presentation in Blue Green Lined Styl...

Ecosystem Interactions Class Discussion Presentation in Blue Green Lined Styl...
Z Score,T Score, Percential Rank and Box Plot Graph

Z Score,T Score, Percential Rank and Box Plot Graph
Russian Call Girls in Andheri Airport Mumbai WhatsApp 9167673311 💞 Full Nigh...

Russian Call Girls in Andheri Airport Mumbai WhatsApp 9167673311 💞 Full Nigh...
Separation of Lanthanides/ Lanthanides and Actinides

Separation of Lanthanides/ Lanthanides and Actinides
Measures of Dispersion and Variability: Range, QD, AD and SD

Measures of Dispersion and Variability: Range, QD, AD and SD