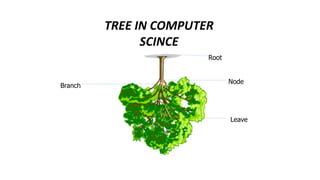
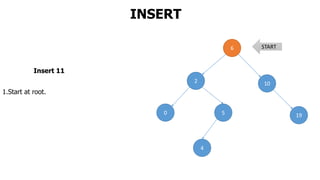
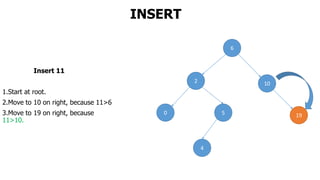
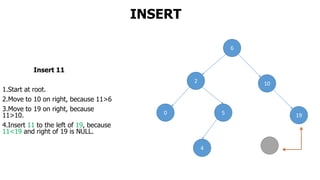
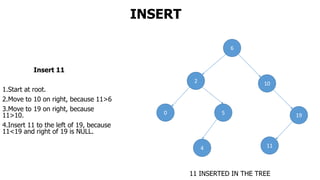
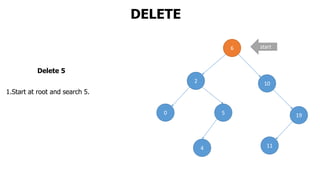
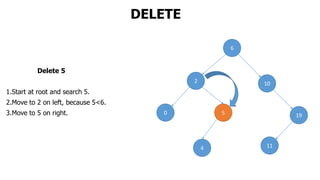
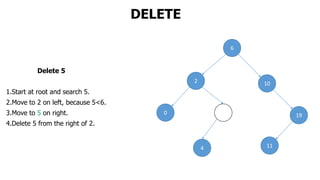
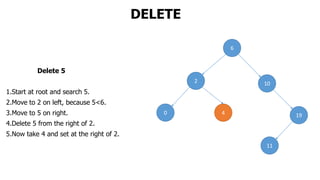
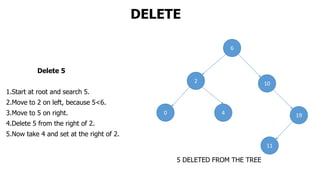
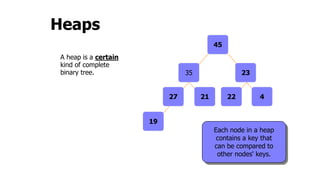
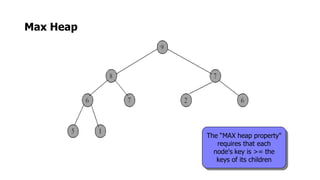
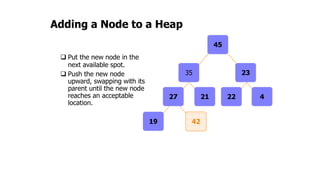
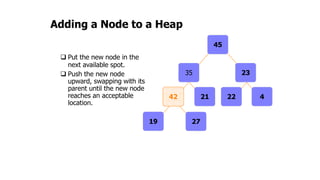
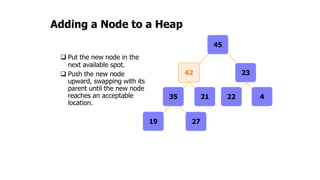
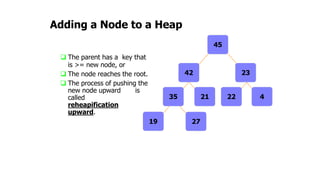
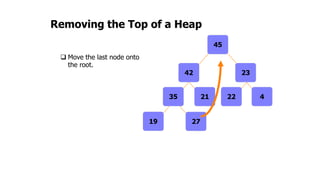
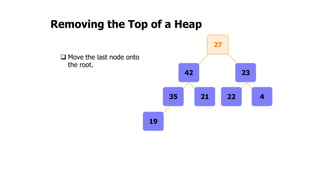
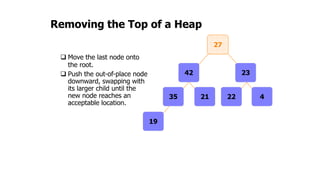
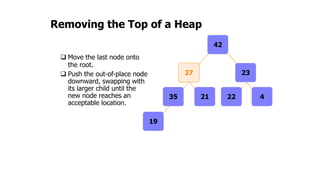
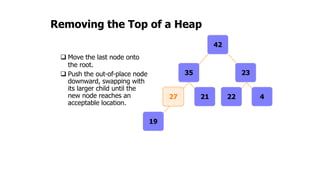
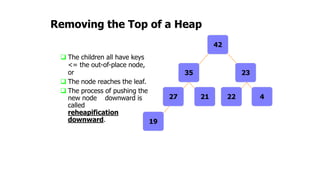
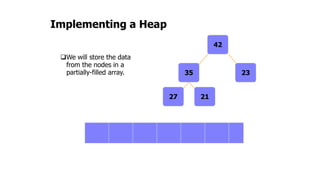
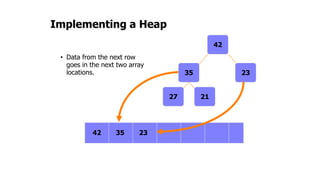
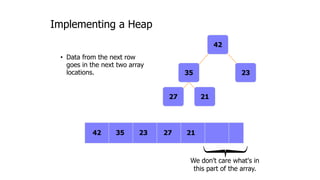
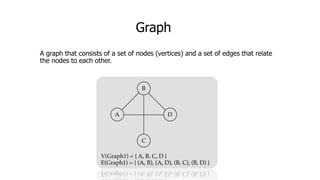
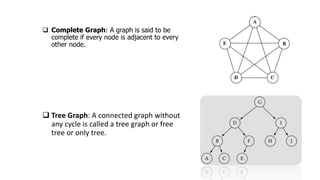
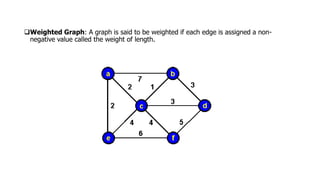
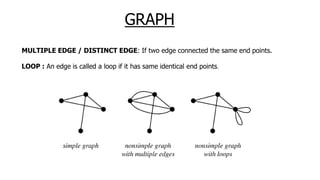
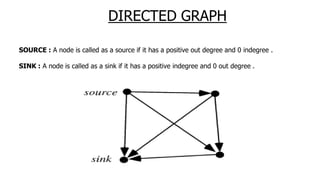
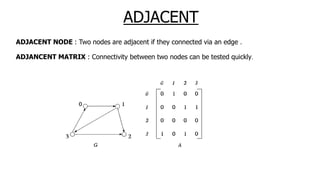
The document provides an overview of various data structures in computer science, including trees, binary search trees, heaps, and graphs. It explains key concepts such as node types, tree operations, heap properties, and graph characteristics like connected and complete graphs. Additionally, it covers insertion and deletion operations for binary search trees and heaps, as well as various representations of graphs.

1. TORU-LOTA
TREE,BST,HEAP,GRAPH

2. TREE

3. TREE IN COMPUTER
SCINCE
Root
Node
Leave
Branch

4. Root: node without parent (A)
Siblings: nodes share the same
parent
Internal node: node with at least
one child.
External node (leaf ): node
without children
Ancestors of a node: parent,
grandparent, grand-grandparent,
etc.
Descendant of a node: child,
grandchild, grand-grandchild, etc.
Depth of a node: number of
ancestors
Height of a tree: maximum depth
of any node
Degree of a node: the number of
its children
Degree of a tree: the maximum
number of its node.

5. Tree Operation

6. BINARY SEARCH TREE

7. Short form of BST is Binary Search TREE
A binary search tree is a binary tree where each node has
a Comparable key the key in any node is larger than the
keys in all nodes in that node's left sub tree and smaller
than the keys in all nodes in that node's right sub tree.
8
6 28
1 5 3525
A COMPLETE BINARY TREE
What is a binary search tree?

8. INSERT
Insert 11
1.Start at root.
6
2 10
0 5 19
4
START

9. INSERT
Insert 11
1.Start at root.
2.Move to 10 on right, because 11>6
6
2 10
0 5 19
4

10. INSERT
Insert 11
1.Start at root.
2.Move to 10 on right, because 11>6
3.Move to 19 on right, because
11>10.
6
2 10
0 5 19
4

11. INSERT
Insert 11
1.Start at root.
2.Move to 10 on right, because 11>6
3.Move to 19 on right, because
11>10.
4.Insert 11 to the left of 19, because
11<19 and right of 19 is NULL.
6
2 10
0 5 19
4

12. INSERT
Insert 11
1.Start at root.
2.Move to 10 on right, because 11>6
3.Move to 19 on right, because
11>10.
4.Insert 11 to the left of 19, because
11<19 and right of 19 is NULL.
6
2 10
0 5 19
4 11

13. INSERT
Insert 11
1.Start at root.
2.Move to 10 on right, because 11>6
3.Move to 19 on right, because
11>10.
4.Insert 11 to the left of 19, because
11<19 and right of 19 is NULL.
6
2 10
0 5 19
4 11
11 INSERTED IN THE TREE

14. DELETE
Delete 5
1.Start at root and search 5.
6
2 10
0 5 19
4 11
start

15. DELETE
Delete 5
1.Start at root and search 5.
2.Move to 2 on left, because 5<6.
6
2 10
0 5 19
4 11

16. DELETE
Delete 5
1.Start at root and search 5.
2.Move to 2 on left, because 5<6.
3.Move to 5 on right.
6
2 10
0 5 19
4 11

17. DELETE
Delete 5
1.Start at root and search 5.
2.Move to 2 on left, because 5<6.
3.Move to 5 on right.
4.Delete 5 from the right of 2.
6
2 10
0 19
4 11

18. DELETE
Delete 5
1.Start at root and search 5.
2.Move to 2 on left, because 5<6.
3.Move to 5 on right.
4.Delete 5 from the right of 2.
5.Now take 4 and set at the right of 2.
6
2 10
0 4 19
11

19. DELETE
Delete 5
1.Start at root and search 5.
2.Move to 2 on left, because 5<6.
3.Move to 5 on right.
4.Delete 5 from the right of 2.
5.Now take 4 and set at the right of 2.
6
2 10
0 4 19
11
5 DELETED FROM THE TREE

20. TRAVERSING
Preorder:
1.Visit the Root
2.Traverse the Left subtree
3.Traverse The Right subtree
7>1>0>3>2>5>4>6>9>8>10
In order:
1.Traverse the Left subtree.
2.Visit the Root.
3.Traverse the Right subtree.
Post Order :
1.Traverse the Left subtree
2. Traverse the Right subtree.
3.Visit the Root.
7
1 9
0 3
8 10
52
64
7,1,0,3,2,5,4,6,9,8,10

21. Heaps
A heap is a certain
kind of complete
binary tree.
Each node in a heap
contains a key that
can be compared to
other nodes' keys.
19
4222127
23
45
35

22. Types of Heaps:
• There are two types of heaps
1. Max Heap
2. Min Heap

23. 23
Max Heap
The “MAX heap property"
requires that each
node's key is >= the
keys of its children

24. 24
Min Heap
The “Min heap property"
requires that each
node's key is <= the
keys of its children

25. Adding a Node to a Heap
 Put the new node in the
next available spot.
 Push the new node
upward, swapping with its
parent until the new node
reaches an acceptable
location.
19
4222127
23
45
35
42

26. Adding a Node to a Heap
 Put the new node in the
next available spot.
 Push the new node
upward, swapping with its
parent until the new node
reaches an acceptable
location.
19
4222142
23
45
35
27

27. Adding a Node to a Heap
 Put the new node in the
next available spot.
 Push the new node
upward, swapping with its
parent until the new node
reaches an acceptable
location.
19
4222135
23
45
42
27

28. Adding a Node to a Heap
 The parent has a key that
is >= new node, or
 The node reaches the root.
 The process of pushing the
new node upward is
called
reheapification
upward.
19
4222135
23
45
42
27

29. Removing the Top of a Heap
 Move the last node onto
the root.
19
4222135
23
45
42
27

30. Removing the Top of a Heap
 Move the last node onto
the root.
19
4222135
23
27
42

31. Removing the Top of a Heap
 Move the last node onto
the root.
 Push the out-of-place node
downward, swapping with
its larger child until the
new node reaches an
acceptable location.
19
4222135
23
27
42

32. Removing the Top of a Heap
 Move the last node onto
the root.
 Push the out-of-place node
downward, swapping with
its larger child until the
new node reaches an
acceptable location.
19
4222135
23
42
27

33. Removing the Top of a Heap
 Move the last node onto
the root.
 Push the out-of-place node
downward, swapping with
its larger child until the
new node reaches an
acceptable location.
19
4222127
23
42
35

34. Removing the Top of a Heap
 The children all have keys
<= the out-of-place node,
or
 The node reaches the leaf.
 The process of pushing the
new node downward is
called
reheapification
downward. 19
4222127
23
42
35

35. Implementing a Heap
We will store the data
from the nodes in a
partially-filled array.
An array of data
2127
23
42
35

36. Implementing a Heap
• Data from the root goes in
the first location of
the array.
An array of data
2127
23
42
35
42

37. Implementing a Heap
• Data from the next row
goes in the next two array
locations.
An array of data
2127
23
42
35
42 35 23

38. Implementing a Heap
• Data from the next row
goes in the next two array
locations.
An array of data
2127
23
42
35
42 35 23 27 21

39. Implementing a Heap
• Data from the next row
goes in the next two array
locations.
An array of data
2127
23
42
35
42 35 23 27 21
We don't care what's in
this part of the array.

40. Graph
A graph that consists of a set of nodes (vertices) and a set of edges that relate
the nodes to each other.

41.  Degree: The number of edge of a node is called degree of that node.
 Connected Graph: A graph said to be connected if and only if there is a
simple path between two nodes.

42.  Complete Graph: A graph is said to be
complete if every node is adjacent to every
other node.
 Tree Graph: A connected graph without
any cycle is called a tree graph or free
tree or only tree.

43.  Cycle: Cycle is a closed simple path with
length three or more.
Here,ACDA is a cycle in this Graph.
 Labeled Graph: A graph is said to be
labeled if its edegs are assigned data.

44. Weighted Graph: A graph is said to be weighted if each edge is assigned a non-
negative value called the weight of length.

45. GRAPH
MULTIPLE EDGE / DISTINCT EDGE: If two edge connected the same end points.
LOOP : An edge is called a loop if it has same identical end points.

46. DIRECTED GRAPG
DIRECTED GRAPH : In a graph the vertices that are connected together , where all the edges are
directed from one two another vertices .
From this graph v1 is initial points and v2 is terminal points.
v1 is a predecessor of v2 and v2 is successer of v1 .
DEGREE : Directed graph has two types degree .
• Indegree
• Outdegree

47. DIRECTED GRAPH
SOURCE : A node is called as a source if it has a positive out degree and 0 indegree .
SINK : A node is called as a sink if it has a positive indegree and 0 out degree .

48. ADJACENT NODE : Two nodes are adjacent if they connected via an edge .
ADJANCENT MATRIX : Connectivity between two nodes can be tested quickly.
ADJACENT

49. ADJACENT
ADJACENT LIST : Adjacent node can be represented also adjacent list.
• 0 -> 1
• 1 -> 2 , 3
• 2 ->
• 3 -> 0 , 2

50. THANK YOU