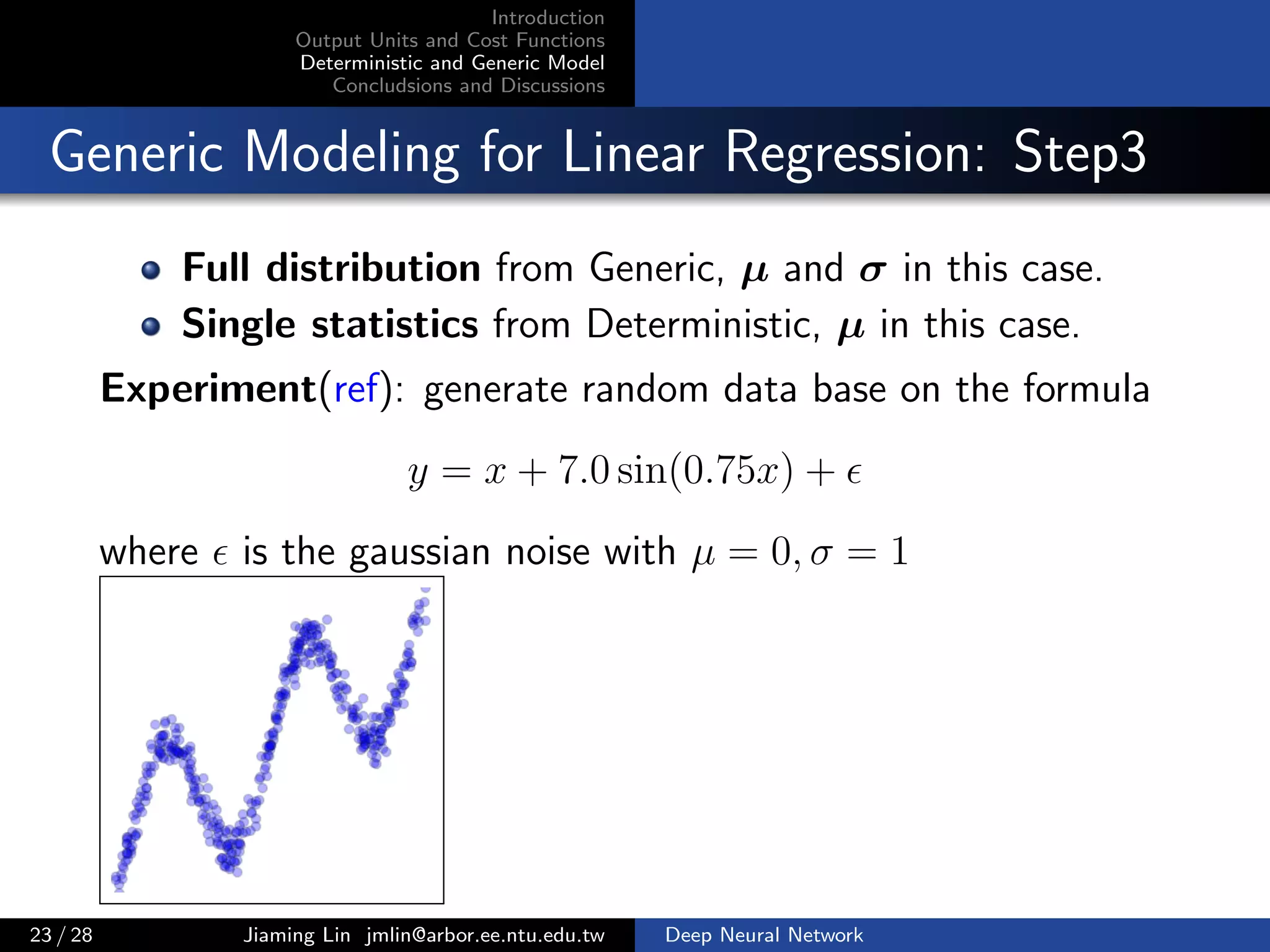
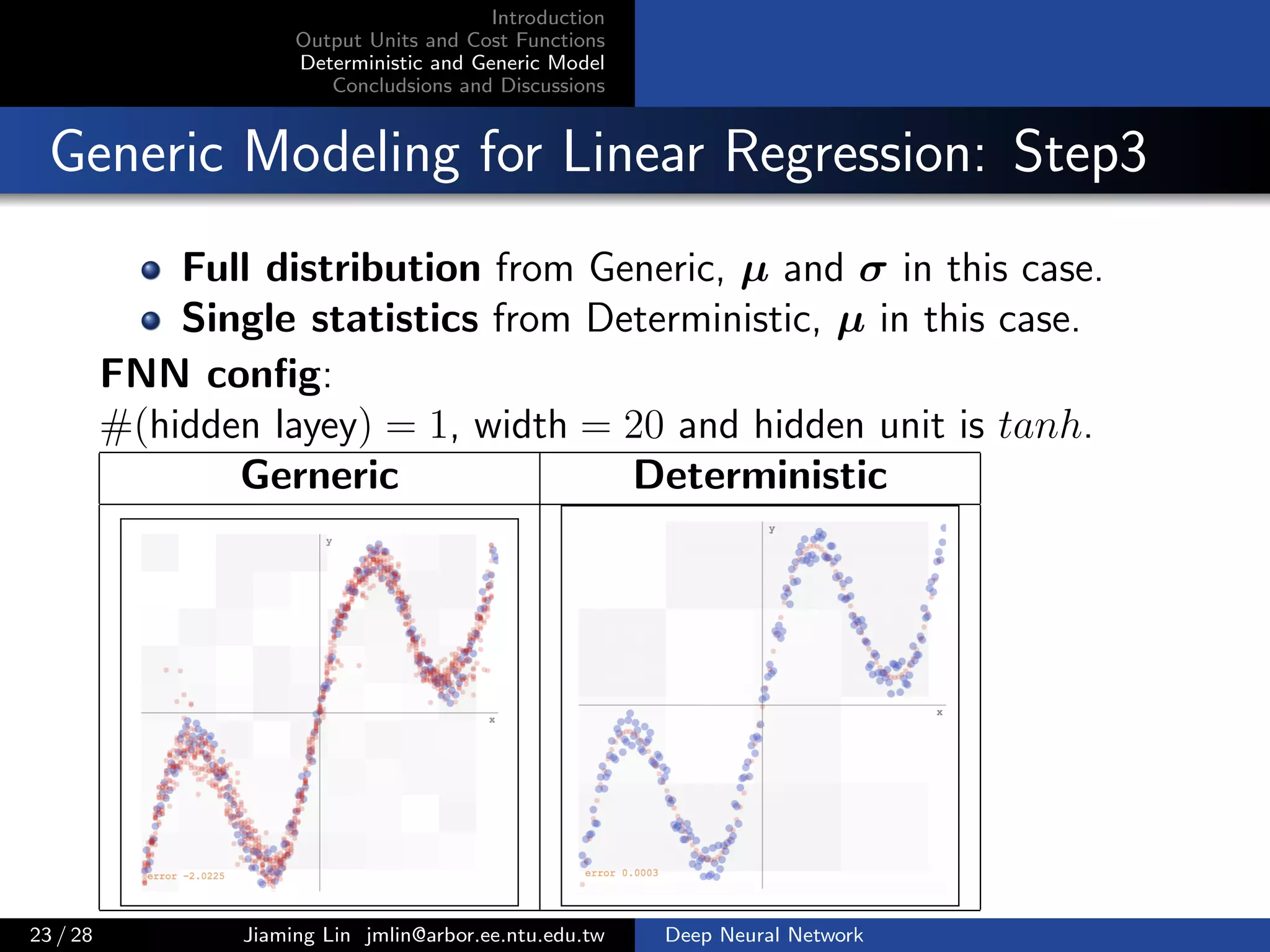
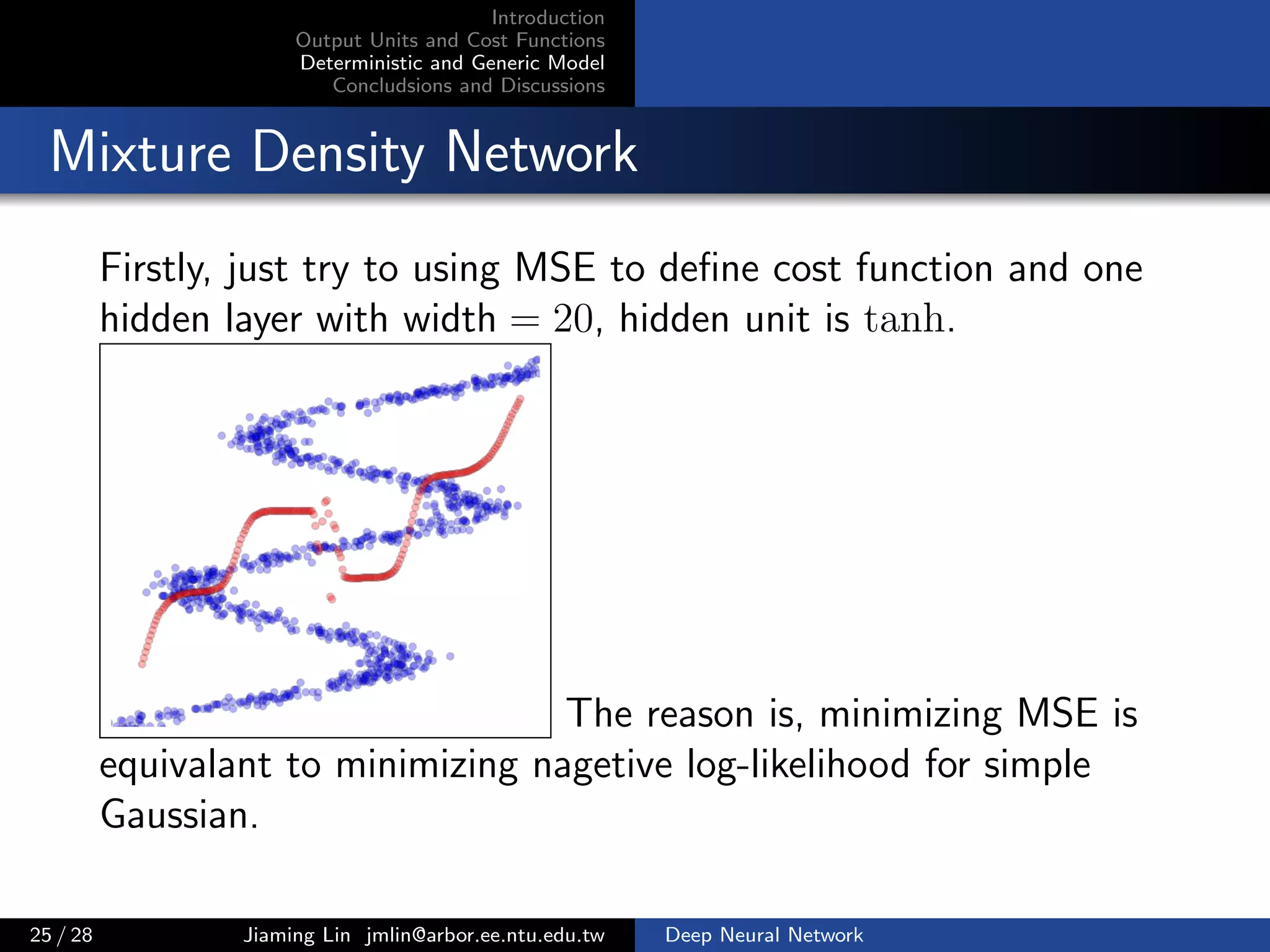
The document discusses the selection of output units and cost functions in deep neural networks, emphasizing criteria for classification and regression tasks. It evaluates two predominant cost functions: mean square error and cross entropy, comparing their analyticity and learning ability. The document further extends the discussion to multinoulli classification, detailing the cost function derivation and properties necessary for efficient learning and function stability.












![Introduction
Output Units and Cost Functions
Deterministic and Generic Model
Concludsions and Discussions
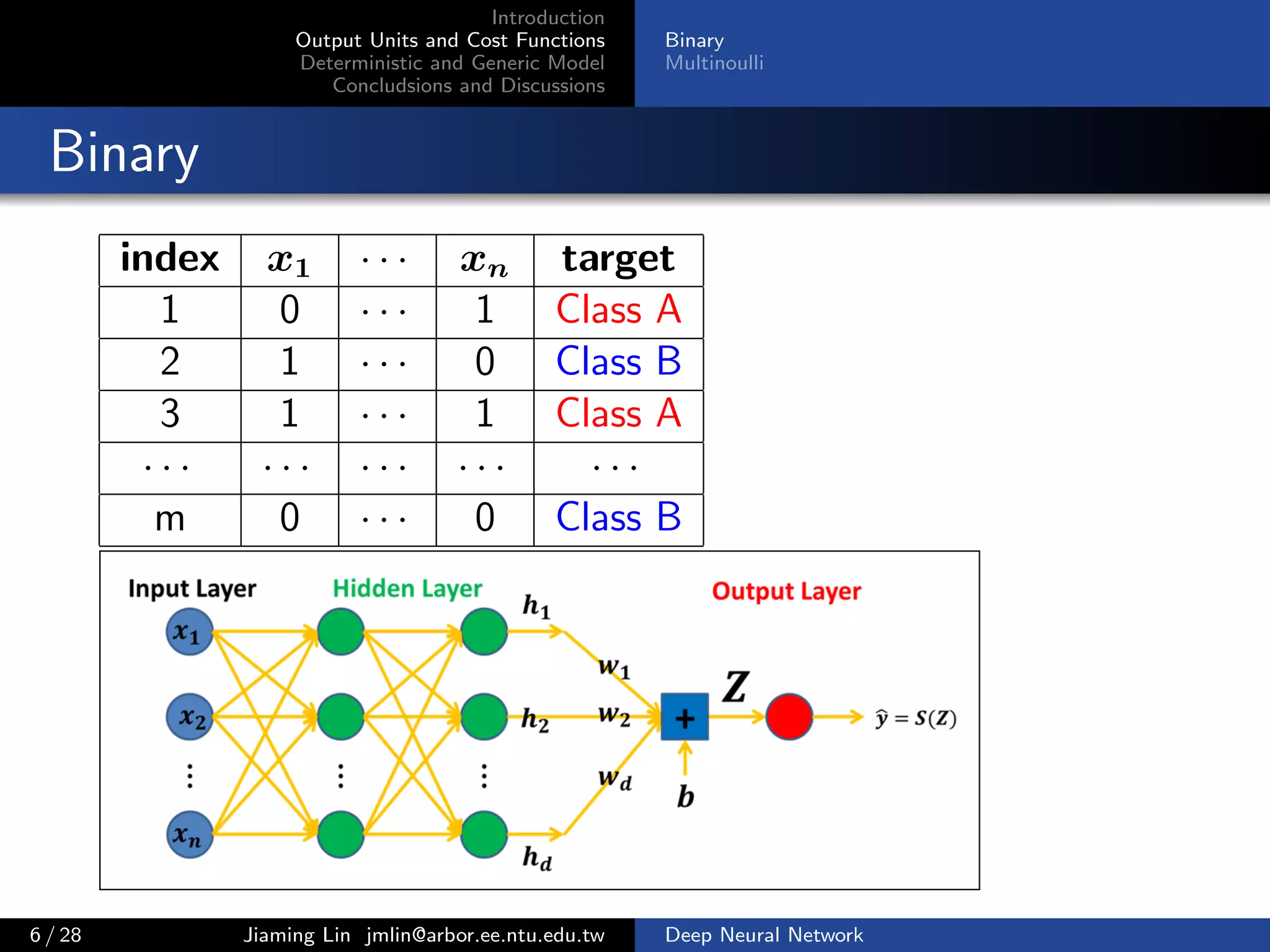
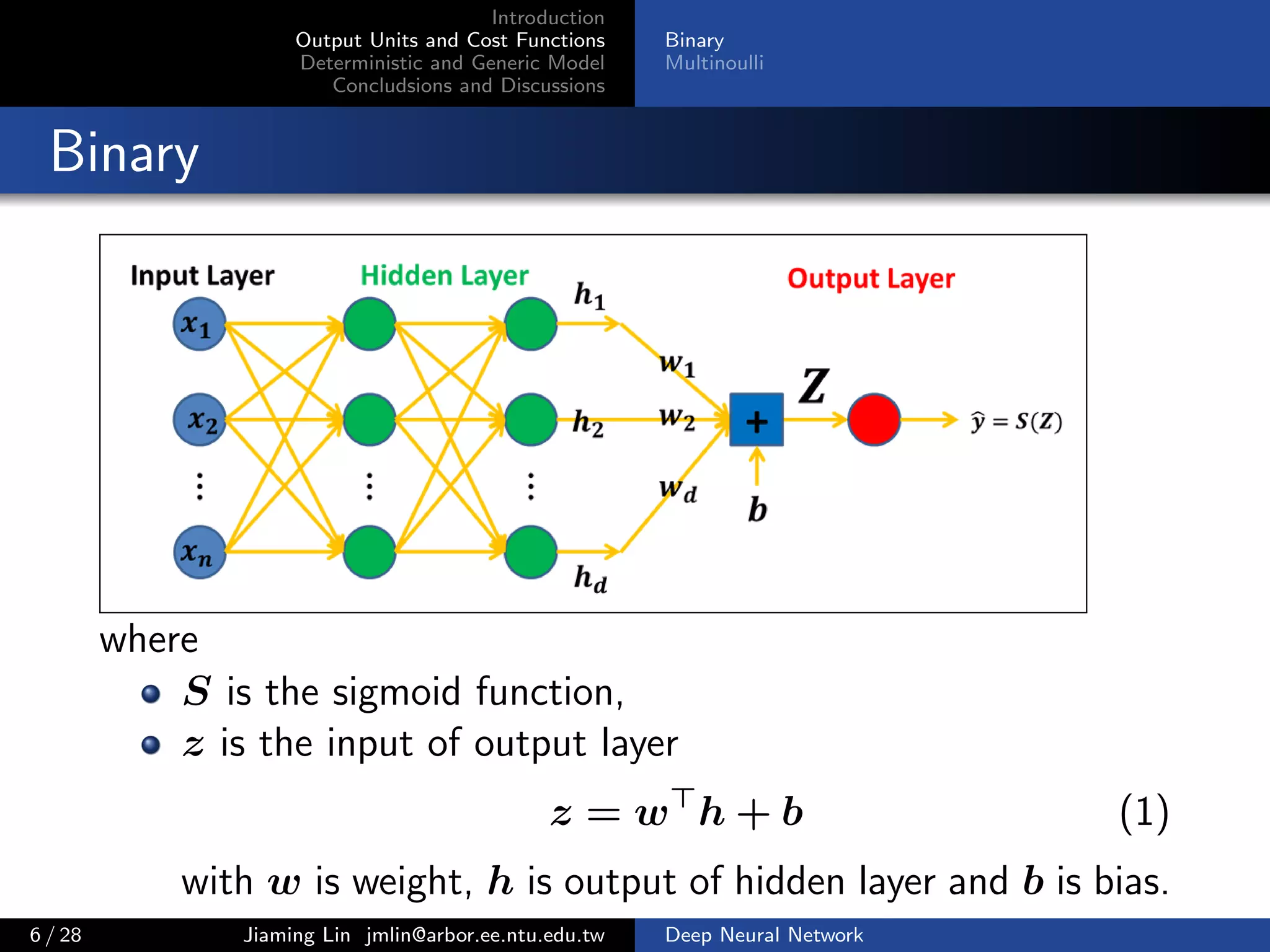
Binary
Multinoulli
Comparison between MSE and Cross Entropy
Learning Ability: compare the gradients
∂Cmse
∂w
= [S(z) − y] [1 − S(z)] S(z)h, (3)
∂Cce
∂w
= [y − S(z)] h (4)
respectively, where S is sigmoid, z = w h + b.
8 / 28 Jiaming Lin jmlin@arbor.ee.ntu.edu.tw Deep Neural Network](https://image.slidesharecdn.com/fnnoutputcost-170109103653/75/Output-Units-and-Cost-Function-in-FNN-15-2048.jpg)
![Introduction
Output Units and Cost Functions
Deterministic and Generic Model
Concludsions and Discussions
Binary
Multinoulli
Comparison between MSE and Cross Entropy
MSE Cross Entropy
[S(z) − y] [1 − S(z)] S(z)h [y − S(z)] h
If y = 1 and ˆy → 1,
steps → 0
If y = 1 and ˆy → 0,
steps → 0
If y = 0 and ˆy → 1,
steps → 0
If y = 0 and ˆy → 0,
steps → 0
If y = 1 and ˆy → 1,
steps → 0
If y = 1 and ˆy → 0,
steps → 1
If y = 0 and ˆy → 1,
steps → −1
If y = 0 and ˆy → 0,
steps → 0
9 / 28 Jiaming Lin jmlin@arbor.ee.ntu.edu.tw Deep Neural Network](https://image.slidesharecdn.com/fnnoutputcost-170109103653/75/Output-Units-and-Cost-Function-in-FNN-16-2048.jpg)
![Introduction
Output Units and Cost Functions
Deterministic and Generic Model
Concludsions and Discussions
Binary
Multinoulli
Comparison between MSE and Cross Entropy
MSE Cross Entropy
[S(z) − y] [1 − S(z)] S(z)h [y − S(z)] h
If y = 1 and ˆy → 1,
steps → 0
If y = 1 and ˆy → 0,
steps → 0
If y = 0 and ˆy → 1,
steps → 0
If y = 0 and ˆy → 0,
steps → 0
If y = 1 and ˆy → 1,
steps → 0
If y = 1 and ˆy → 0,
steps → 1
If y = 0 and ˆy → 1,
steps → −1
If y = 0 and ˆy → 0,
steps → 0
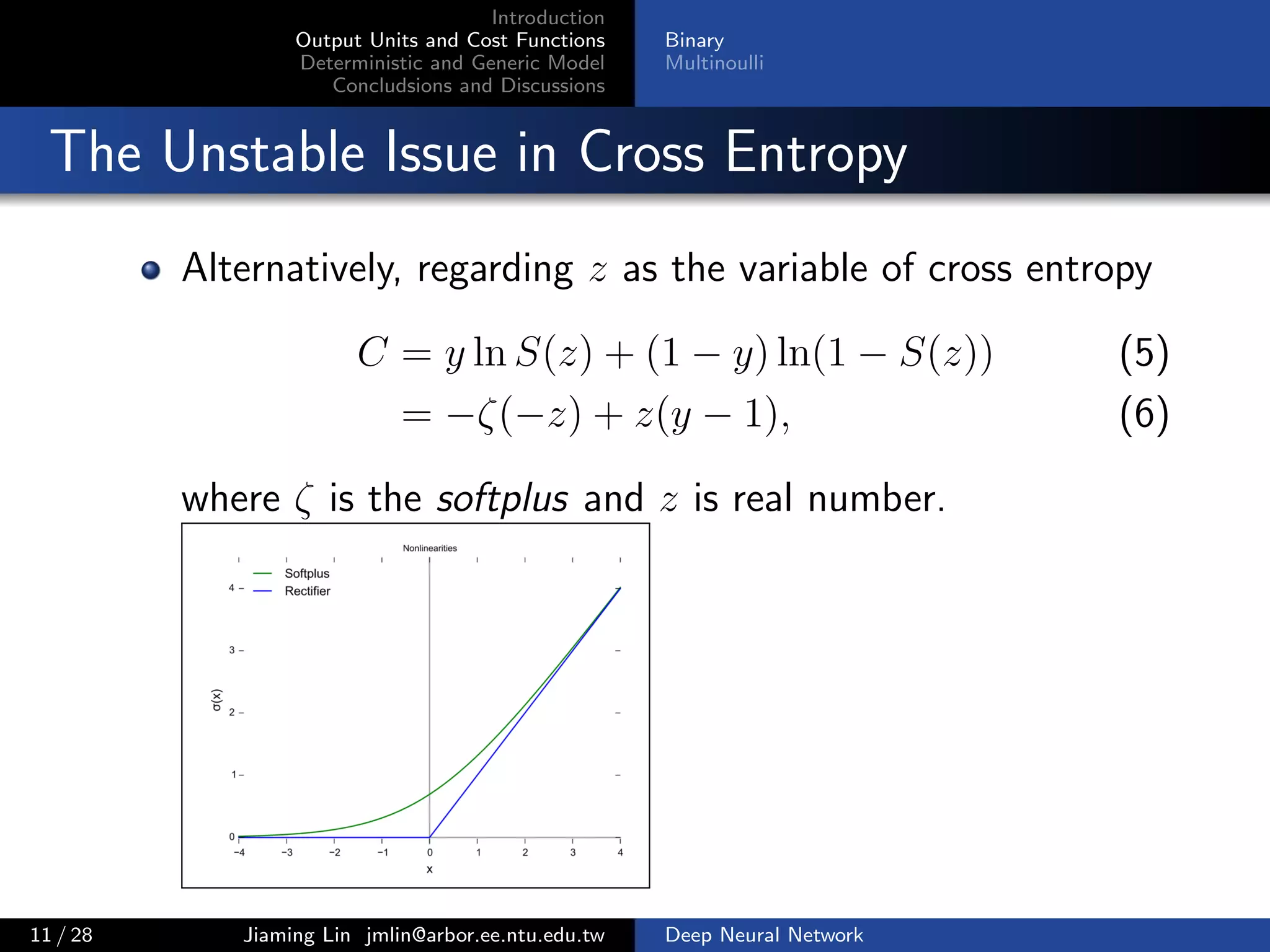
In the ceas of Mean Square Error, the progress get stuck when
z is very positive or very negative.
9 / 28 Jiaming Lin jmlin@arbor.ee.ntu.edu.tw Deep Neural Network](https://image.slidesharecdn.com/fnnoutputcost-170109103653/75/Output-Units-and-Cost-Function-in-FNN-17-2048.jpg)








![Introduction
Output Units and Cost Functions
Deterministic and Generic Model
Concludsions and Discussions
Binary
Multinoulli
A Lemma for Cost Function Simplify
Analyticity(infinitely differentiable)
Learning ability(first order derivatives)
To claim above properties, We should show a lemma at very
first,
Lemma 1
For the output z = w h + b and z = [z1, . . . , zK], we have
sup
z
ln
K
j=1
exp(zj) = max
j
{zj}. (8)
14 / 28 Jiaming Lin jmlin@arbor.ee.ntu.edu.tw Deep Neural Network](https://image.slidesharecdn.com/fnnoutputcost-170109103653/75/Output-Units-and-Cost-Function-in-FNN-27-2048.jpg)










![Introduction
Output Units and Cost Functions
Deterministic and Generic Model
Concludsions and Discussions
Generic Modeling for Linear Regression: Step1
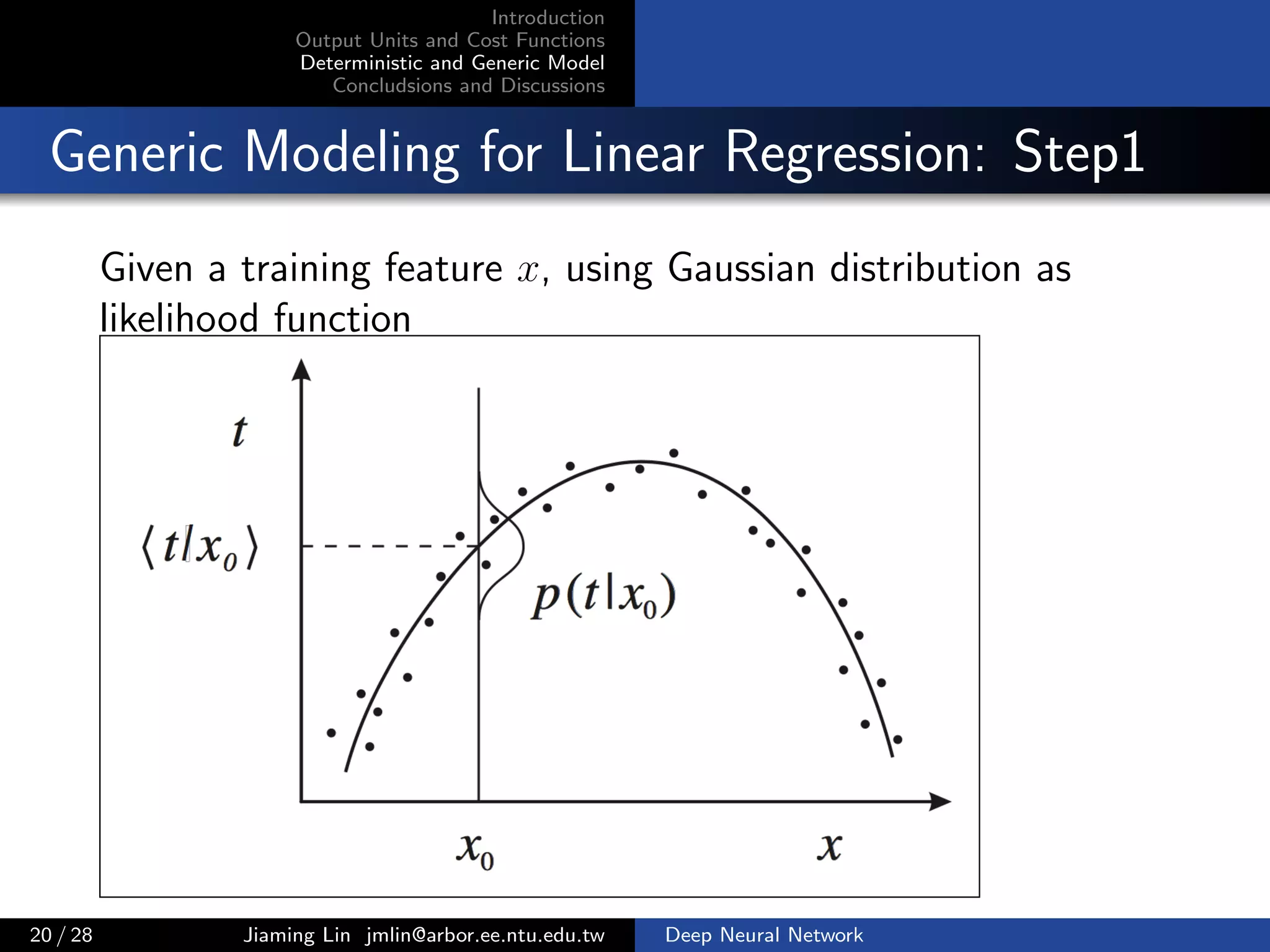
Given a training feature x, using Gaussian distribution as
likelihood function
p(y | x) =
1
√
2σ2π
exp
−(µ − y)2
2σ2
,
where we denote the output of hidden layer as hx, weight
w = [w1, w2] and bias b = [b1, b2], then
µ = w1 hx + b1
σ = w2 hx + b2
Intuitively, µ and σ are two linear output units, they are
functions of x.
20 / 28 Jiaming Lin jmlin@arbor.ee.ntu.edu.tw Deep Neural Network](https://image.slidesharecdn.com/fnnoutputcost-170109103653/75/Output-Units-and-Cost-Function-in-FNN-39-2048.jpg)