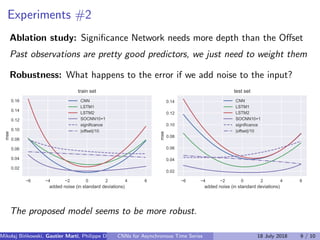
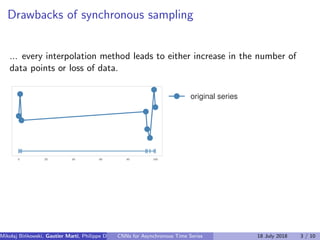
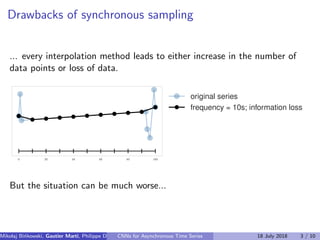
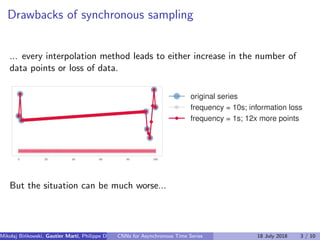
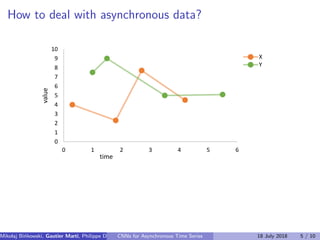
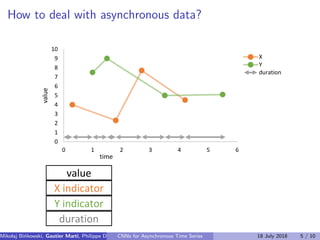
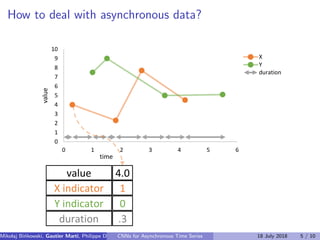
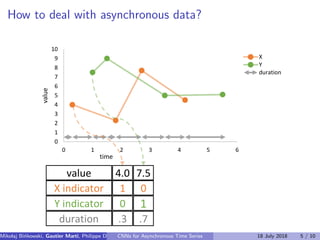
The document discusses the challenges of modeling asynchronous time series data, noting the limitations of traditional interpolation methods which lead to data loss or increase in data points. It presents a proposed architecture that combines autoregressive models with data-dependent weights to improve prediction accuracy for asynchronous data. The authors aim to find a neural network architecture suitable for effectively representing and analyzing such data.

1. Autoregressive Convolutional Neural Networks for
Asynchronous Time Series
Hong Kong Machine Learning Meetup - Season 1 Episode 1
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat
Imperial College London, Ecole Polytechnique, Hellebore Capital
18 July 2018
HELLEBORECAPITAL
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 1 / 10

2. Introduction
Problem: Many real-world time series are asynchronous, i.e.
the durations between consecutive observations are irregular/random
or
the separate dimensions are not observed simultaneously.
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 2 / 10

3. Introduction
Problem: Many real-world time series are asynchronous, i.e.
the durations between consecutive observations are irregular/random
or
the separate dimensions are not observed simultaneously.
At the same time:
time series models usually require both regularity of observations and
simultaneous sampling of all dimensions,
continuous-time models often require simultaneous sampling.
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 2 / 10

4. Introduction
Problem: Many real-world time series are asynchronous, i.e.
the durations between consecutive observations are irregular/random
or
the separate dimensions are not observed simultaneously.
At the same time:
time series models usually require both regularity of observations and
simultaneous sampling of all dimensions,
continuous-time models often require simultaneous sampling.
Numerous interpolation methods have been developed for preprocessing of
asynchronous series. However,...
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 2 / 10

5. Drawbacks of synchronous sampling
... every interpolation method leads to either increase in the number of
data points or loss of data.
0 20 40 60 80 100
original series
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 3 / 10

6. Drawbacks of synchronous sampling
... every interpolation method leads to either increase in the number of
data points or loss of data.
0 20 40 60 80 100
original series
frequency = 10s; information loss
But the situation can be much worse...
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 3 / 10

7. Drawbacks of synchronous sampling
... every interpolation method leads to either increase in the number of
data points or loss of data.
0 20 40 60 80 100
original series
frequency = 10s; information loss
frequency = 1s; 12x more points
But the situation can be much worse...
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 3 / 10

8. Drawbacks of synchronous sampling
WLPH
SULFH
HYROXWLRQRITXRWHGSULFHVWKURXJKRXWRQHGD
VRXUFH$ELG
VRXUFH$DVN
VRXUFH%ELG
VRXUFH%DVN
VRXUFHELG
VRXUFHDVN
VRXUFH'ELG
VRXUFH'DVN
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 4 / 10

9. Drawbacks of synchronous sampling
WLPH
SULFH
HYROXWLRQRITXRWHGSULFHVWKURXJKRXWRQHGD
VRXUFH$ELG
VRXUFH$DVN
VRXUFH%ELG
VRXUFH%DVN
VRXUFHELG
VRXUFHDVN
VRXUFH'ELG
VRXUFH'DVN
Objectives:
Propose alternative representation of asynchronous data,
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 4 / 10

10. Drawbacks of synchronous sampling
WLPH
SULFH
HYROXWLRQRITXRWHGSULFHVWKURXJKRXWRQHGD
VRXUFH$ELG
VRXUFH$DVN
VRXUFH%ELG
VRXUFH%DVN
VRXUFHELG
VRXUFHDVN
VRXUFH'ELG
VRXUFH'DVN
Objectives:
Propose alternative representation of asynchronous data,
Find neural network architecture appropriate for such representation.
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 4 / 10

11. How to deal with asynchronous data?
0 0.3 1 1.5 1.8 2.7 3.5 4.20.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6
value
time
X
Y
duration
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 5 / 10

12. How to deal with asynchronous data?
0 0.3 1 1.5 1.8 2.7 3.5 4.20.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6
value
time
X
Y
duration
X indicator
value
Y indicator
duration
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 5 / 10

13. How to deal with asynchronous data?
0 0.3 1 1.5 1.8 2.7 3.5 4.20.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6
value
time
X
Y
duration
1
4.0
0
.3
X indicator
value
Y indicator
duration
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 5 / 10

14. How to deal with asynchronous data?
0 0.3 1 1.5 1.8 2.7 3.5 4.20.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6
value
time
X
Y
duration
1
4.0 7.5
0
0 1
.3 .7
X indicator
value
Y indicator
duration
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 5 / 10

15. How to deal with asynchronous data?
0 0.3 1 1.5 1.8 2.7 3.5 4.20.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6
value
time
X
Y
duration
1
1
4.0 7.5
0
0 1
.3 .7
9.0 2.3
0 1
1 0
.5 .3
7.7 5.0
1 0
0 1
.9 .6
4.5 5.1
1 0
0
.7 1.3
X indicator
value
Y indicator
duration
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 5 / 10

16. Not satisfactory performance of Neural Nets
Architectures such as Long-Short Term Memory (LSTM) and
Convolutional Neural Networks (CNN) do not perform as well as expected,
compared to simple autoregressive (AR) model
Xn =
M
m=1
Xn−m × am + εn (1)
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 6 / 10

17. Not satisfactory performance of Neural Nets
Architectures such as Long-Short Term Memory (LSTM) and
Convolutional Neural Networks (CNN) do not perform as well as expected,
compared to simple autoregressive (AR) model.
Idea: equip AR model with data-dependent weights
Xn =
M
m=1
Xn−m × am(Xn−m) + εn (1)
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 6 / 10

18. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

19. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

20. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

21. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

22. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
Offset networkSignificance network
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

23. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
Convolution
kx1 kernel
c channels
Convolution
1x1 kernel
c channels
Offset networkSignificance network
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

24. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
× (𝑵 𝑺 − 𝟏) layers
Convolution
kx1 kernel
c channels
× (𝑵 𝒐𝒇𝒇 − 𝟏) layers
Convolution
1x1 kernel
c channels
Offset networkSignificance network
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

25. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
× (𝑵 𝑺 − 𝟏) layers
Convolution
kx1 kernel
c channels
Convolution
1x1 kernel
dI channels
Convolution
kx1 kernel
dI channels
× (𝑵 𝒐𝒇𝒇 − 𝟏) layers
Convolution
1x1 kernel
c channels
Offset networkSignificance network
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

26. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
× (𝑵 𝑺 − 𝟏) layers
Convolution
kx1 kernel
c channels
Convolution
1x1 kernel
dI channels
Convolution
kx1 kernel
dI channels
× (𝑵 𝒐𝒇𝒇 − 𝟏) layers
Convolution
1x1 kernel
c channels
Offset network
𝒙𝑰
Significance network
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
𝐨𝐟𝐟
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

27. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
Weighting
𝑯 𝒏−𝟏 = 𝝈 𝑺 ⨂ (𝐨𝐟𝐟 + 𝒙 𝑰
)
× (𝑵 𝑺 − 𝟏) layers
Convolution
kx1 kernel
c channels
𝑺
𝛔
Convolution
1x1 kernel
dI channels
Convolution
kx1 kernel
dI channels
× (𝑵 𝒐𝒇𝒇 − 𝟏) layers
Convolution
1x1 kernel
c channels
Offset network
𝒙𝑰
Significance network
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
𝐨𝐟𝐟
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

28. Proposed Architecture
The model predicts
yn = E[xI
n|x−M
n ],
where
x−M
n = (xn−1, . . . , xn−M)
- regressors
I = (i1, i2, . . . , idI
)
- target dimensions
with
ˆyn =
M
m=1
W·,m ⊗ σ(S(x−M
n ))·,m
data dependent weights
⊗ off(xn−m) + xI
n−m
adjusted regressors
Weighting
𝑯 𝒏−𝟏 = 𝝈 𝑺 ⨂ (𝐨𝐟𝐟 + 𝒙 𝑰
)
× (𝑵 𝑺 − 𝟏) layers
Convolution
kx1 kernel
c channels
𝑺
𝛔
Convolution
1x1 kernel
dI channels
Convolution
kx1 kernel
dI channels
× (𝑵 𝒐𝒇𝒇 − 𝟏) layers
Convolution
1x1 kernel
c channels
Offset network
𝒙𝑰
Significance network
Input series 𝒙 𝒕−𝟔 𝒙 𝒕−𝟓 𝒙 𝒕−𝟒 𝒙 𝒕−𝟑 𝒙 𝒕−𝟐 𝒙 𝒕−𝟏
d - dimensional
timesteps
Locally connected layer
fully connected for each of 𝒅𝑰 dimensions
𝑯 𝒏 = 𝑾𝑯 𝒏−𝟏 + 𝒃
𝐨𝐟𝐟
ෝ𝒙 𝒕
𝑰
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 7 / 10

29. Experiments
Datasets:
artificially generated,
synchronous asynchronous
Electricity consumption [UCI
repository]
Quotes [16 tasks]
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 8 / 10

30. Experiments
Datasets:
artificially generated,
synchronous asynchronous
Electricity consumption [UCI
repository]
Quotes [16 tasks]
Benchmarks:
(linear) VAR model
vanilla LSTM, 1d-CNN
25-layer conv. ResNet
Phased LSTM [Neil et al. 2016]
Sync 16 Sync 64 Async 16 Async 64 Electricity Quotes0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
MSE
VAR
CNN
ResNet
LSTM
Phased LSTM
SOCNN (ours)
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 8 / 10

31. Experiments #2
Ablation study: Significance Network needs more depth than the Offset
Past observations are pretty good predictors, we just need to weight them
Mikolaj Bi´nkowski, Gautier Marti, Philippe Donnat (Imperial College)CNNs for Asynchronous Time Series 18 July 2018 9 / 10

32. Experiments #2
Ablation study: Significance Network needs more depth than the Offset
Past observations are pretty good predictors, we just need to weight them
Robustness: What happens to the error if we add noise to the input?
DGGHGQRLVHLQVWDQGDUGGHYLDWLRQV

33. PVH
WUDLQVHW
11
/670
/670
6211
VLJQLILFDQFH
_RIIVHW_
DGGHGQRLVHLQVWDQGDUGGHYLDWLRQV