Embed presentation
Downloaded 45 times

![0
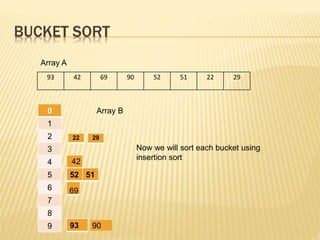
1
2
3
4
5
6
7
8
9
42
51 52
69
22 29
90 93
29 42 51 52 69 90 93
[0] [1] [2] [3] [4] [5] [6] [7]
After sorting each
bucket using
insertion sort
Sorted Array](https://image.slidesharecdn.com/bucketsort-180622135802/85/Bucket-sort-3-320.jpg)
![TIME COMPLEXITY
n=length[A] 1 time
for i=1 to n n times
do insert A[i] into bucket B[n A[i]] O(n)
for i=0 to n-1 n times
do sort bucket B[i] with insertion sort ∑O(n^2)
Concatenate bucket O(n)](https://image.slidesharecdn.com/bucketsort-180622135802/85/Bucket-sort-4-320.jpg)



Bucket sort is an algorithm that works by distributing elements of an array into buckets based on their values. It then sorts each bucket using insertion sort and concatenates the buckets to produce the final sorted array. The time complexity is O(n) to distribute elements into buckets, O(n^2) to sort each bucket using insertion sort, and O(n) to concatenate buckets, resulting in an overall average case time complexity of O(n+k) where n is the number of elements and k is the number of buckets.


![0
1
2
3
4
5
6
7
8
9
42
51 52
69
22 29
90 93
29 42 51 52 69 90 93
[0] [1] [2] [3] [4] [5] [6] [7]
After sorting each
bucket using
insertion sort
Sorted Array](https://image.slidesharecdn.com/bucketsort-180622135802/85/Bucket-sort-3-320.jpg)
![TIME COMPLEXITY
n=length[A] 1 time
for i=1 to n n times
do insert A[i] into bucket B[n A[i]] O(n)
for i=0 to n-1 n times
do sort bucket B[i] with insertion sort ∑O(n^2)
Concatenate bucket O(n)](https://image.slidesharecdn.com/bucketsort-180622135802/85/Bucket-sort-4-320.jpg)


