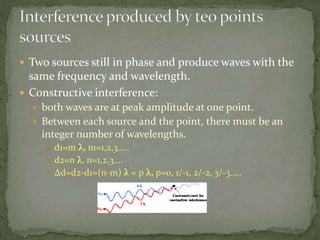
This document discusses two-dimensional wave interference. It defines two waves with the same frequency and wavelength but a fixed phase difference. It describes how constructive interference occurs when the path difference between the two waves is an integer number of wavelengths, resulting in both waves reaching their peak amplitudes at the same point. Locations of constructive and destructive interference are identified in a diagram of circular waves created by two interfering sources.

1. In 2-D waves

2.  The interference of one-dimensional waves which have
the same frequency and wavelength have a fixed phase
difference between the phase constants of the two
waves.

3.  D1(x,t)=A sin(kx- ωt)
 D2(x,t)= A sin(kx- ωt+ φ)
 D(x,t) = 2Acos(φ/2) sin(kx- ωt+ φ/2)

4.  Two sources still in phase and produce waves with the
same frequency and wavelength.
 Constructive interference:
 both waves are at peak amplitude at one point.
 Between each source and the point, there must be an
integer number of wavelengths.
 d1=m λ, m=1,2,3…..
 d2=n λ, n=1,2,3….
 Δd=d2-d1=(n-m) λ = p λ, p=0, 1/-1, 2/-2, 3/-3…..

5.  When one path is an integer number of wavelengths
and the other is a half-integer multiple
 Δd=d2-d1 = (n+1/2) λ

6.  S(r, t) = Sm(r)cos(kr- ωt+ φ)
 r is the distance from the source
 Since the wave in 2-D spreads out over a larger area as it
propagates outward, the amplitude decreases as r
increases.

7.  S(d, t)= Sm(d)cos(kr- ωt+ φ)+ Sm(d)cos(kr- ωt+ φ)
=2Sm(D)cos(kr- ωt+ φ)

8.  Twin water bugs Jimminy and Johnny are both creating a
series of circular waves by jiggling their legs in the water.
The waves undergo interference and create the pattern
represented in the diagram at the right. The thick lines in
the diagram represent wave crests and the thin lines
represent wave troughs. Several of positions in the water
are labeled with a letter. Categorize each labeled position
as being a position where either constructive or destructive
interference occurs.

9.  Constructive Interference: A and B (both at thick
 lines)
 Destructive Interference: C, D, E, and F (stands at one
thick line and one thin line)

10.  Physics 101 textbook (definitions and equations)
 Google pictures
 www.physicsclassroom.com (question)