Embed presentation
Downloaded 213 times





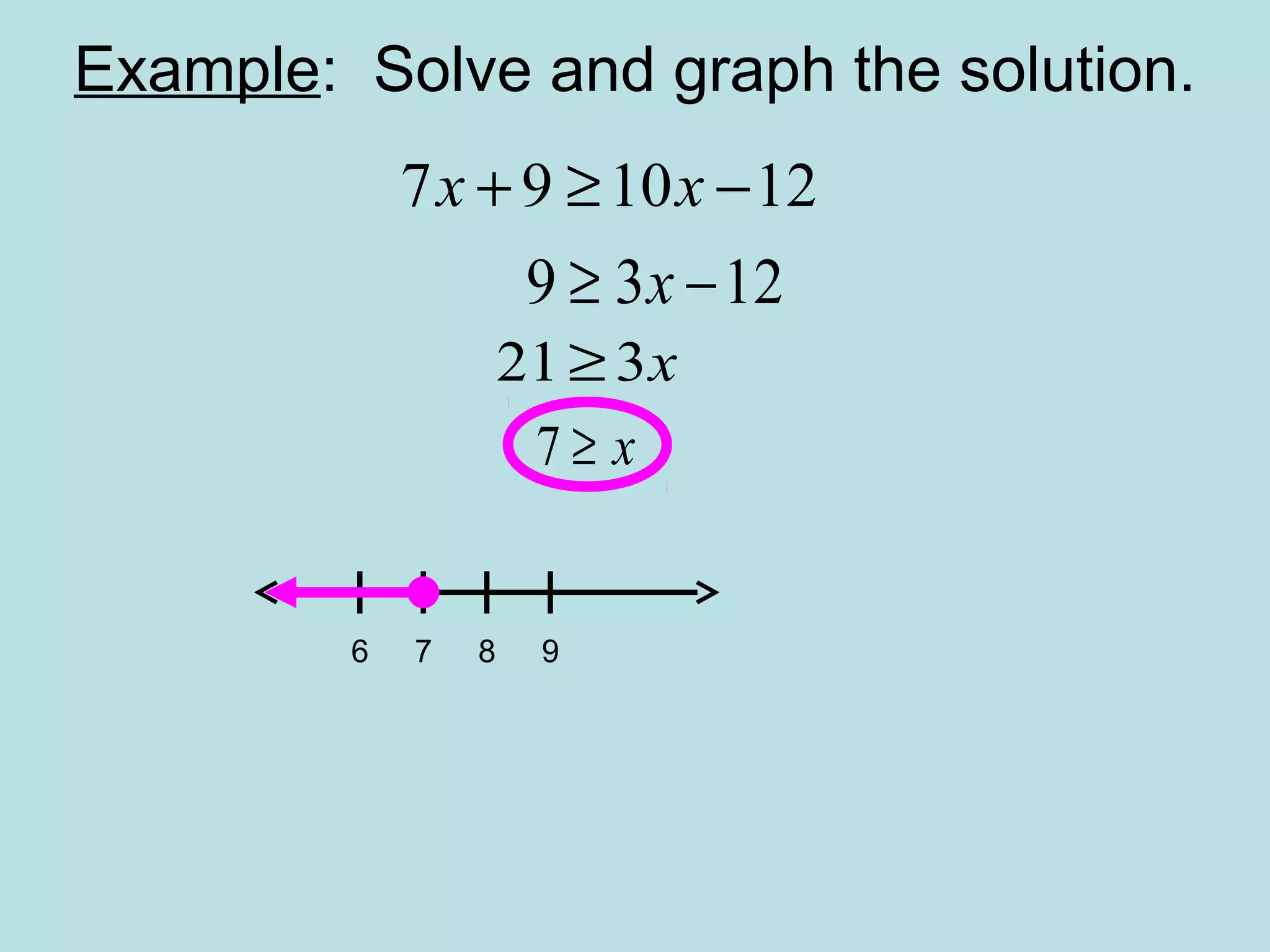
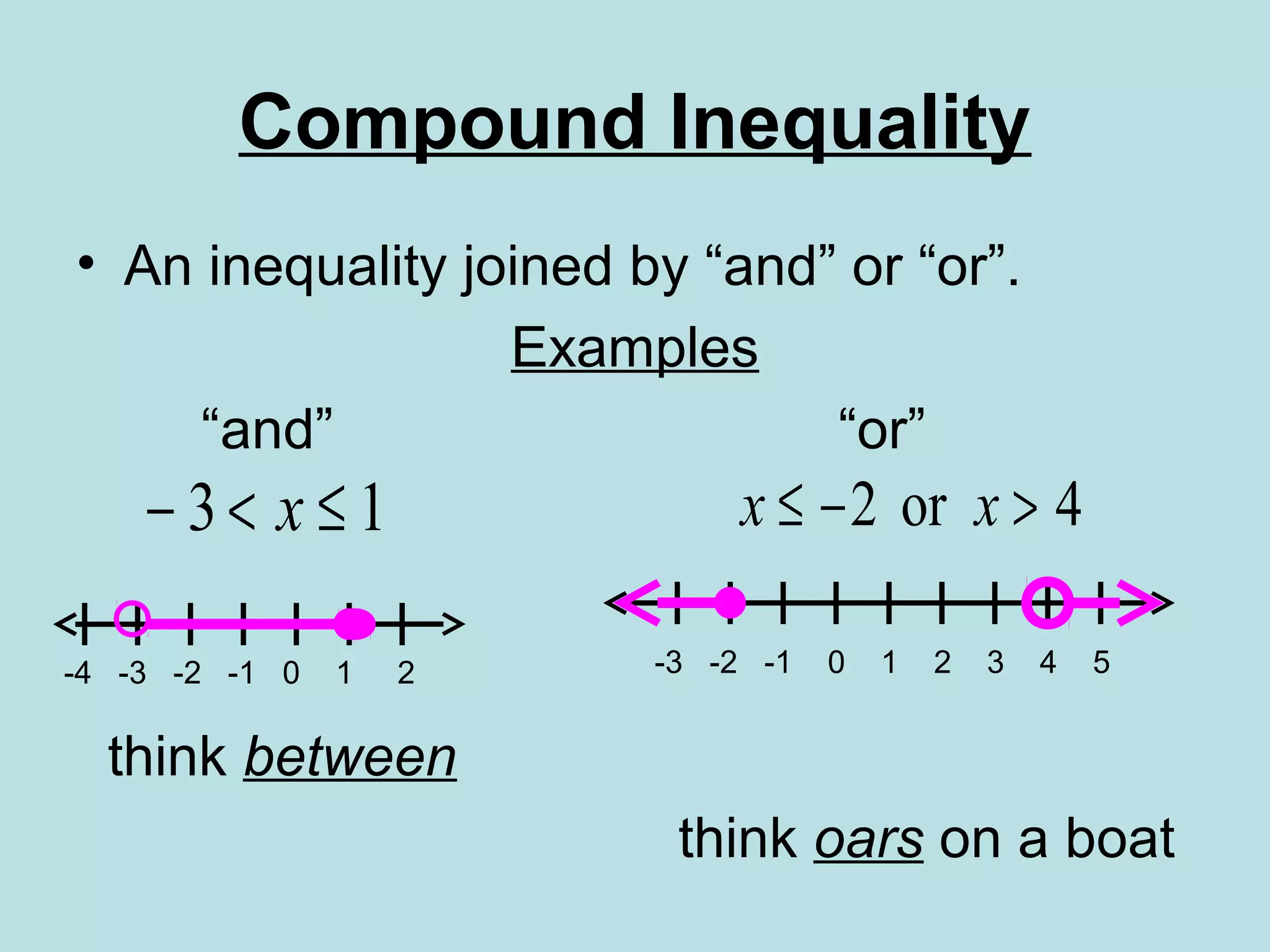

This document discusses solving linear inequalities. It defines inequality symbols and notes that a linear inequality involves one variable to the first power. It explains that a solution makes the inequality true. Transformations can be made to inequalities, such as adding/subtracting the same number or multiplying/dividing by a positive number, but multiplying/dividing by a negative number requires flipping the inequality sign. Graphing linear inequalities involves open or closed dots depending on the inequality sign. Compound inequalities joined by "and" or "or" can be solved by thinking of the solutions between or as oars on a boat.






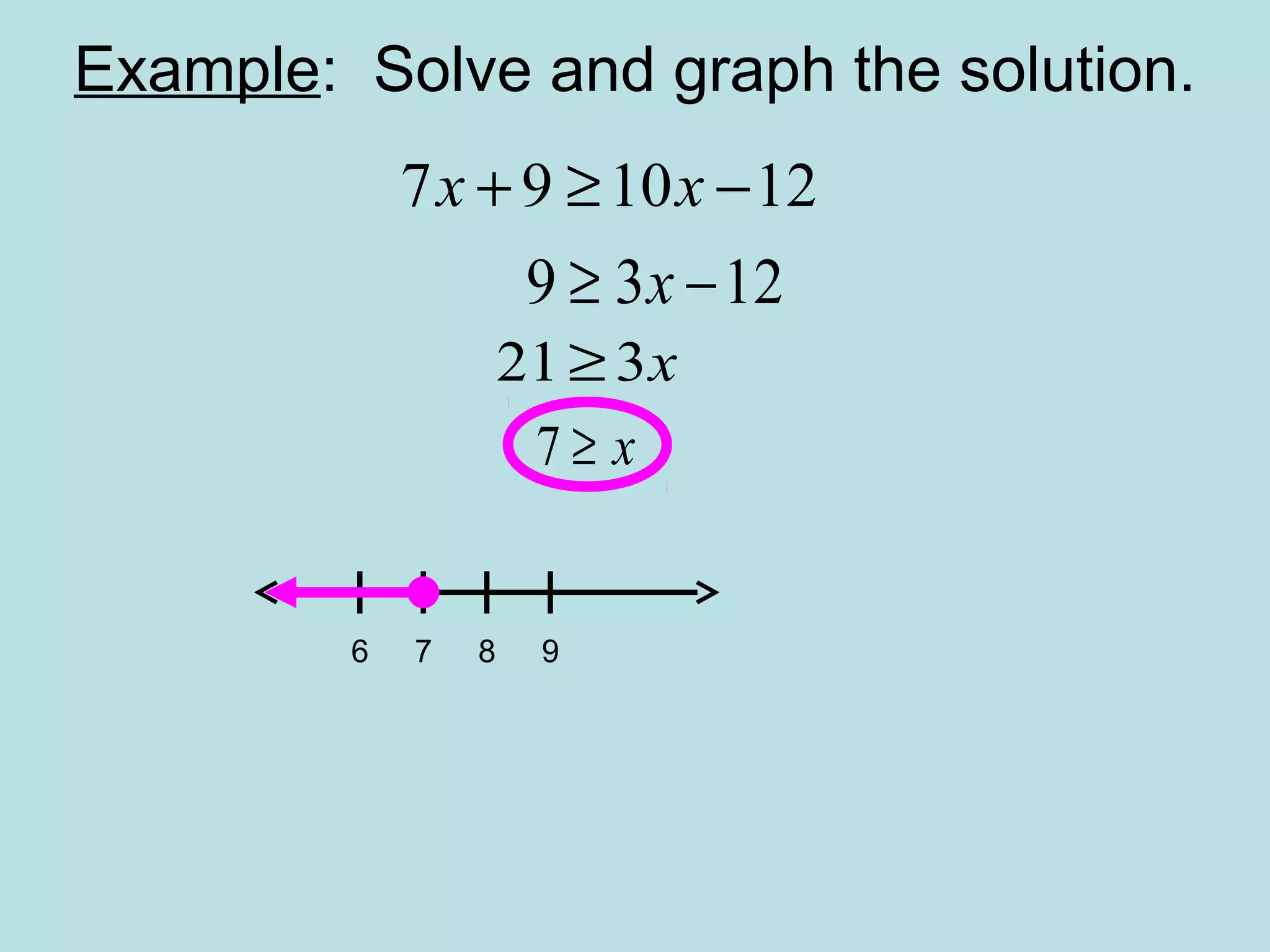
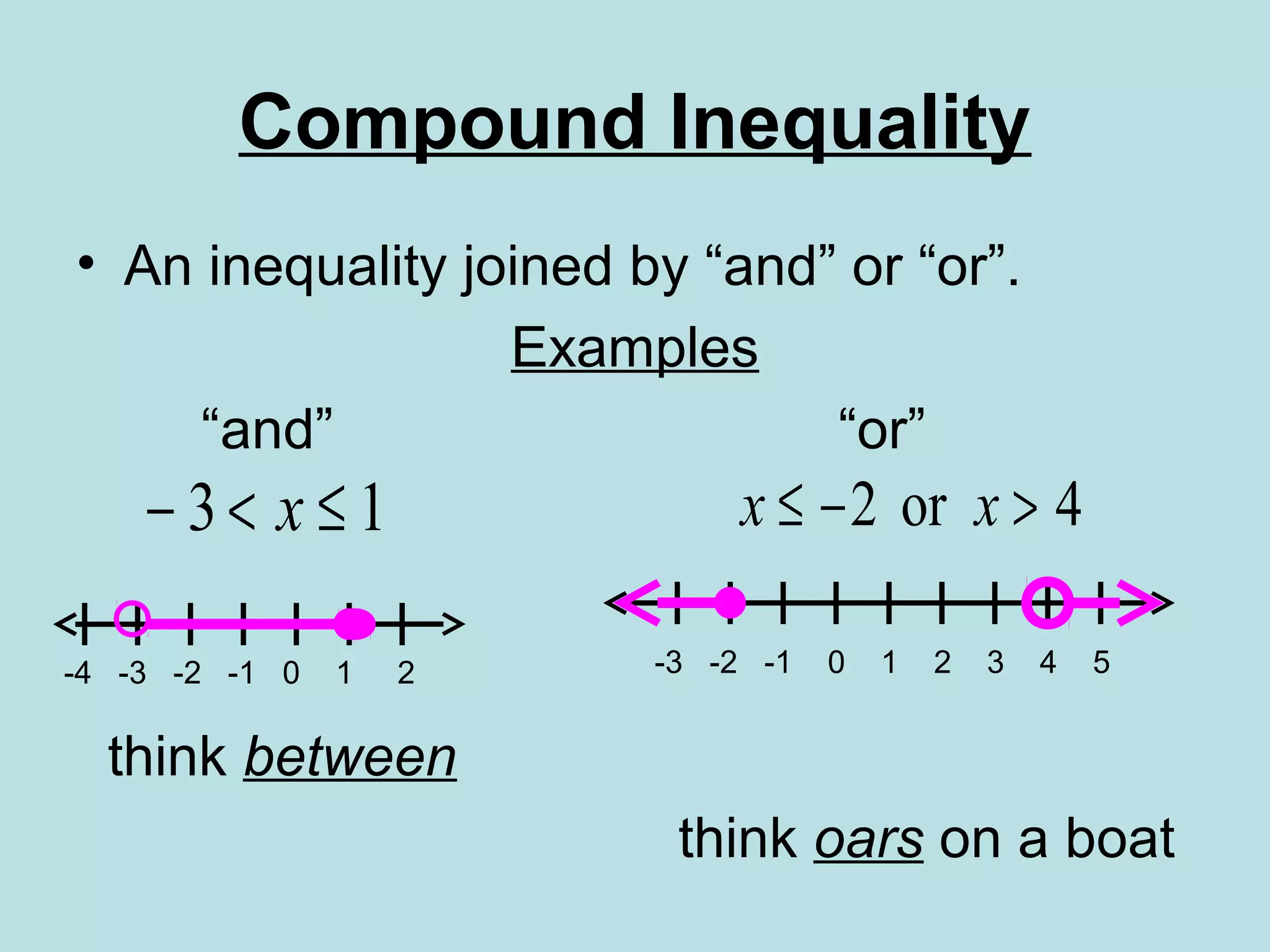


Introduction to the concept of linear inequalities.
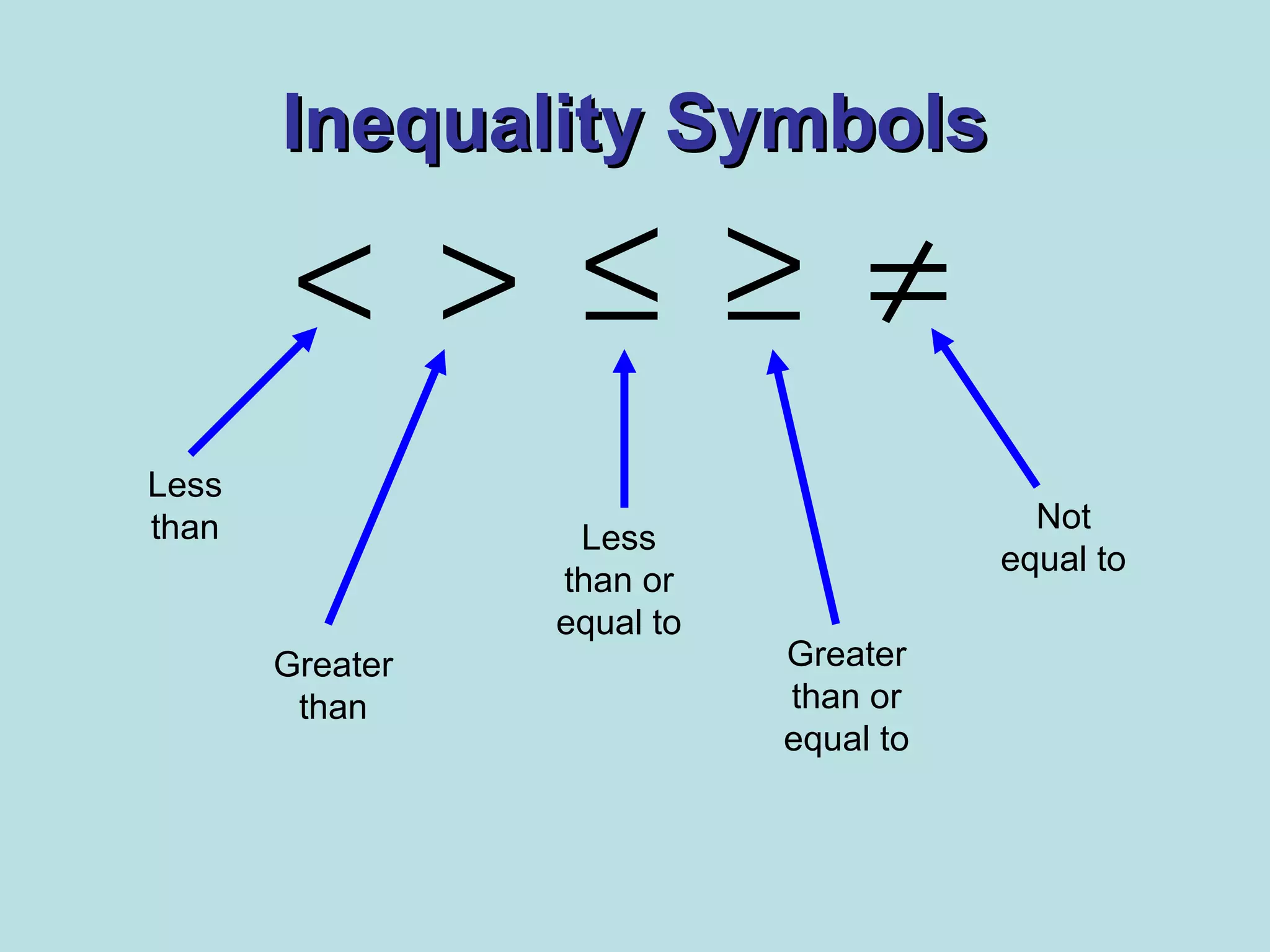
Explanation of inequality symbols: ≠, ≥, ≤, <, >.
A linear inequality is detailed with examples and solutions that satisfy it.
Guidelines on how to manipulate inequalities correctly.
Step-by-step solution of a linear inequality with tips on flipping signs.
Instructions on how to graph linear inequalities with open and closed dots.
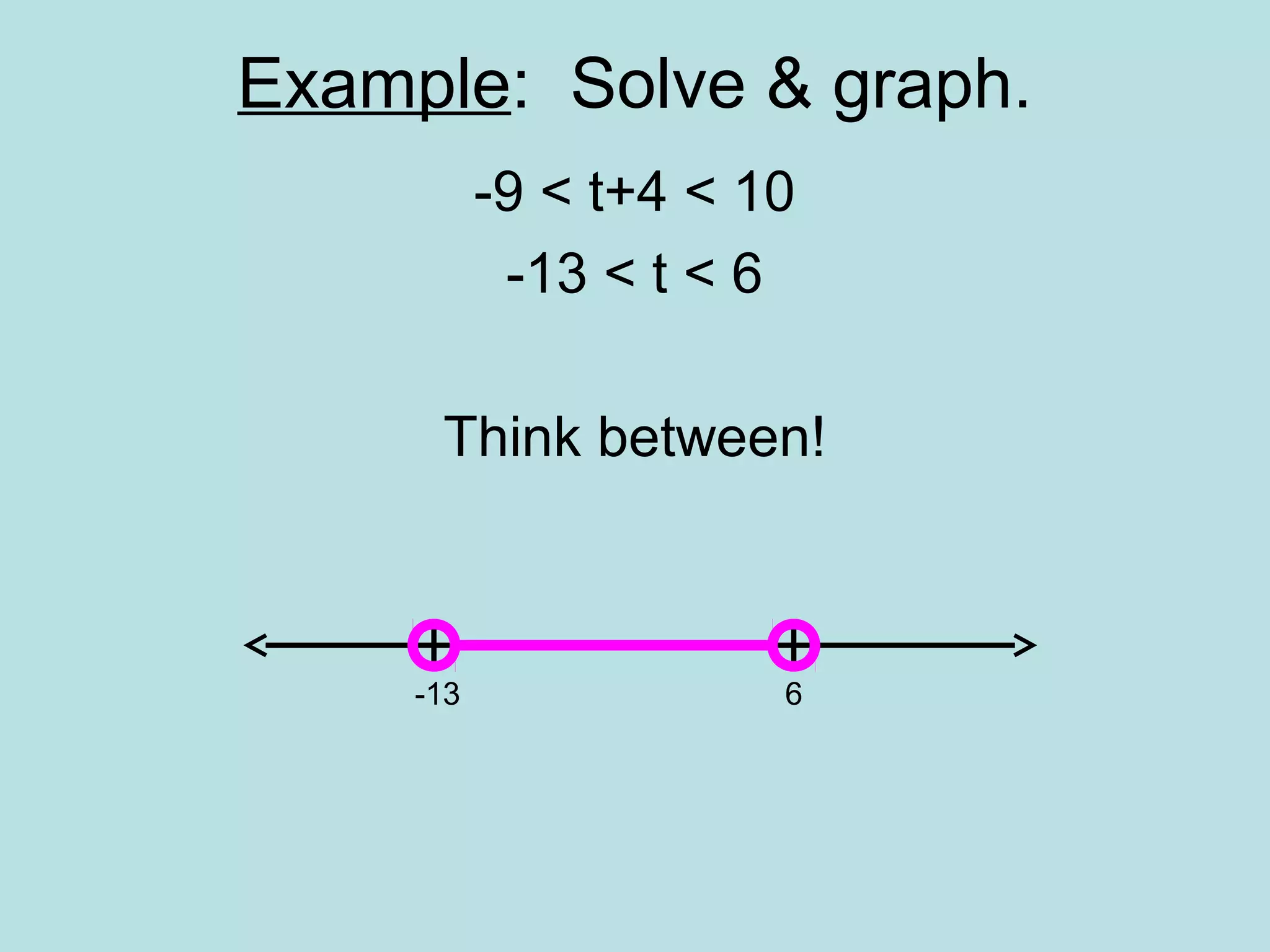
Solve and graph a compound inequality with provided solution.
Definition and examples of compound inequalities using 'and' and 'or'.
Example where a compound inequality is solved and visualized on a graph.
Solution of a compound inequality with clarification on flipping signs.