1. 融合変換による最適化の 理論的基盤と正当性 酒井政裕 慶應義塾大学政策・メディア研究科 修士課程2年

2. 自己紹介 2001年 慶應義塾大学総合政策学部入学 2005年 同卒業 2005年慶應義塾大学大学院 政策・メディア研究科 入学、現在在学中 萩野達也研究室所属

3. 自己紹介: 活動 Haskell Lightweight Language Weekend 2004 Lightweight Language Day and Night 2005 日経ソフトウェア6月号「Haskellによる関数プログラミング入門」 Ruby-GNOME2

4. 研究的興味 関数型言語の最適化 プログラム変換、特に融合変換の 理論的基盤とアルゴリズム

5. 研究の背景 ソフトウェアの不具合が社会問題化するケースが増加 様々な要因 ソフトウェアが必要とされる領域の広がり ソフトウェアの高機能化・多機能化にともなう 複雑化

6. 研究の背景 (2) ソフトウェアの信頼性が重要に 様々なレベルの方法が必要 工学的な品質管理, etc 分かり易い自明なコードが重要 性能のよいコードは複雑で分かり難い 信頼性と効率の両立は難しい

7. 研究の目的 高度な最適化技術の実現 強力な最適化 信頼性を損なわない 信頼性と効率の両立

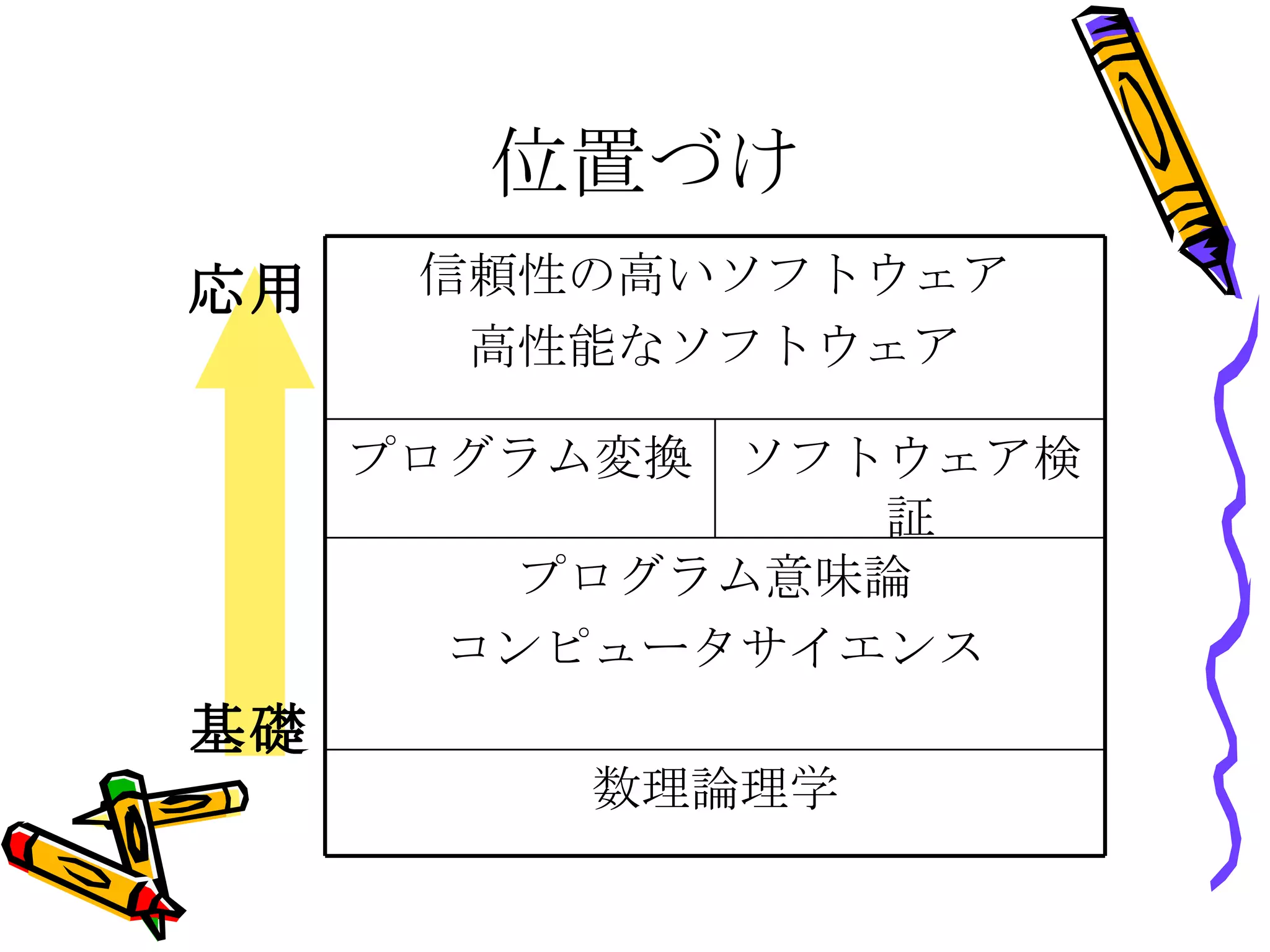
8. 位置づけ 基礎 応用 信頼性の高いソフトウェア 高性能なソフトウェア ソフトウェア検証 プログラム変換 数理論理学 プログラム意味論 コンピュータサイエンス

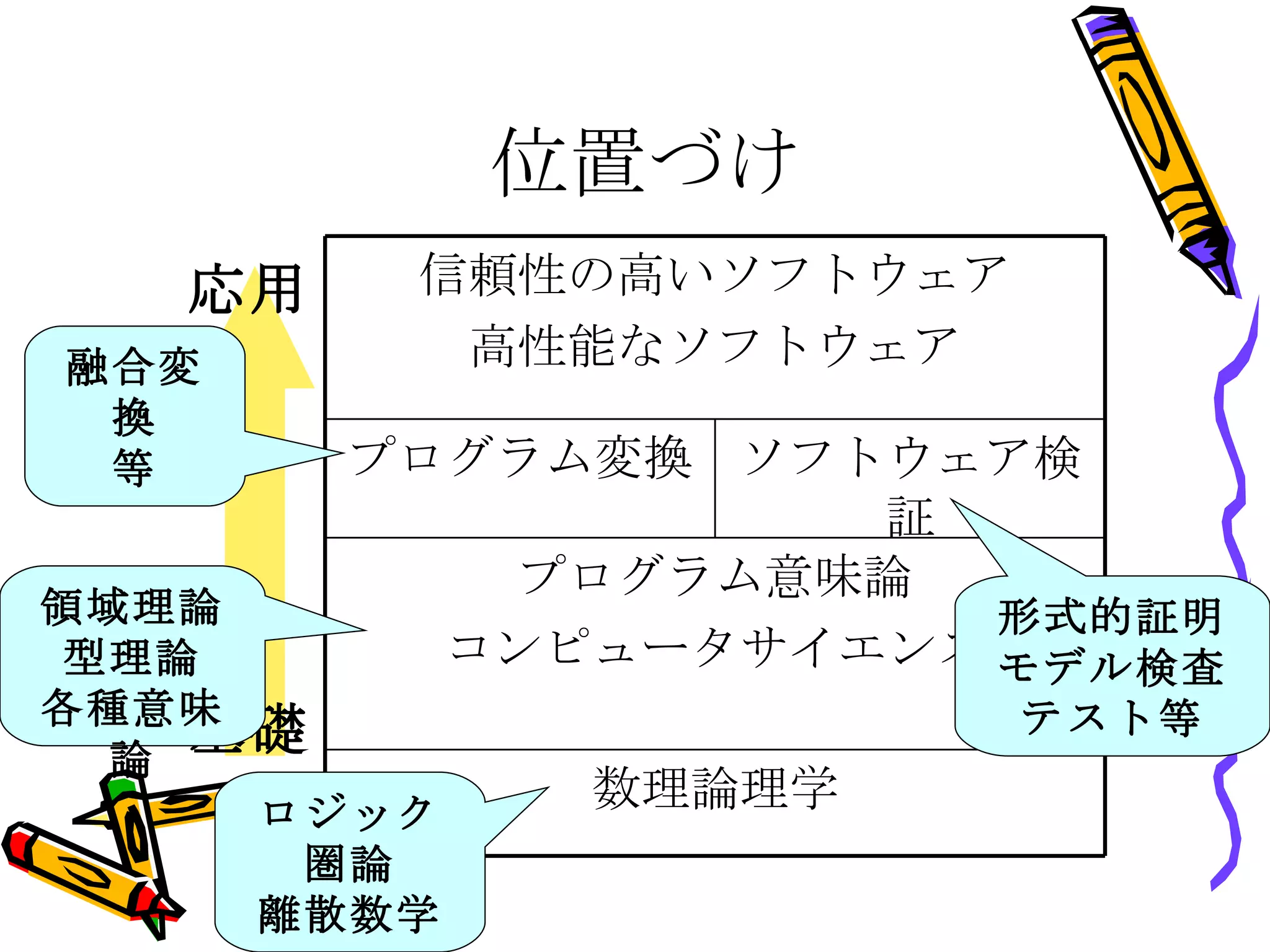
9. 位置づけ 基礎 応用 領域理論 型理論 各種意味論 ロジック 圏論 離散数学 融合変換 等 形式的証明 モデル検査 テスト等 信頼性の高いソフトウェア 高性能なソフトウェア ソフトウェア検証 プログラム変換 数理論理学 プログラム意味論 コンピュータサイエンス

10. プログラム変換と 融合変換

11. 最適化 概念を素直に書いた単純なプログラム 分かりやすい モジュラリティーが高く、扱いやすい しかし、性能が悪いことがしばしば 最適化が必要 コンパイラによる最適化 ハンドチューニング

12. ハンドチューニングの問題 その過程でバグが混入する可能性 結果のプログラムは 複雑で保守が困難 モジュラリティーが低く再利用が困難 信頼性を損なう 最適化のための別アプローチが必要 !

13. プログラム変換 数学的(代数的)な性質を用いる最適化 例) a×3 + a×2 = { 分配則 } a×(3+2) = { calculation } a×5 同じ 意味 で性能のよいプログラムへ変換 中にはオーダが変わるような場合も

14. 融合変換 プログラム変換の一種 複数のパスからなるプログラム わかりやすいが 中間データが存在し、効率が悪い これを単一のパスに変換

15. 融合変換の例 add(vector A, vector B) { vector tmp; for (int i = 0; i < A.dim; i++) { tmp[i] = A[i] + B[i]; } return tmp; } add(add(A,B), C); 二回ループを回す必要

16. 融合変換の例 add3(vector A, vector B, vector C) { vector tmp; for (int i = 0; i < A.dim; i++) { tmp[i] = A[i] + B[i] + C[i]; } return tmp; } add3(A,B,C); 一回のループですむ 効率向上

17. 融合変換 (2) 主に関数型言語で用いられる 中間データ構造を生成しないことによる、空間効率の向上 これまで離れていたコードが接することにより、更なる最適化が適用可能に 時間効率も向上

18. 関数型言語 数学的な関数に基づいた言語 (原則的に)副作用がない 等しい式は自由に置き換えが可能 数学的な取り扱いが容易 例: Haskell, ML, Lisp

19. なぜ関数型言語か? 数学的に厳密な議論をしたい 現状の一般的な命令型言語では難しい 代数的性質が簡単に利用できる 命令型言語では特別な解析が必要 ⇒ そこで、とりあえず関数型言語に特化

20. 関数型言語の代数的性質(例) map 関数 map f [a, b, …] = [f a, f b, …] concat 関数 concat [[a,b], [c], [d,e], ..] = [a,b,c,d,e,…] map f . map g = map (f . g) (map f) . concat = concat . (map (map f))

21. 融合変換の理論 圏論 圏論によるデータ型と帰納的定義 一意性による等式の導出 融合変換の難しさ

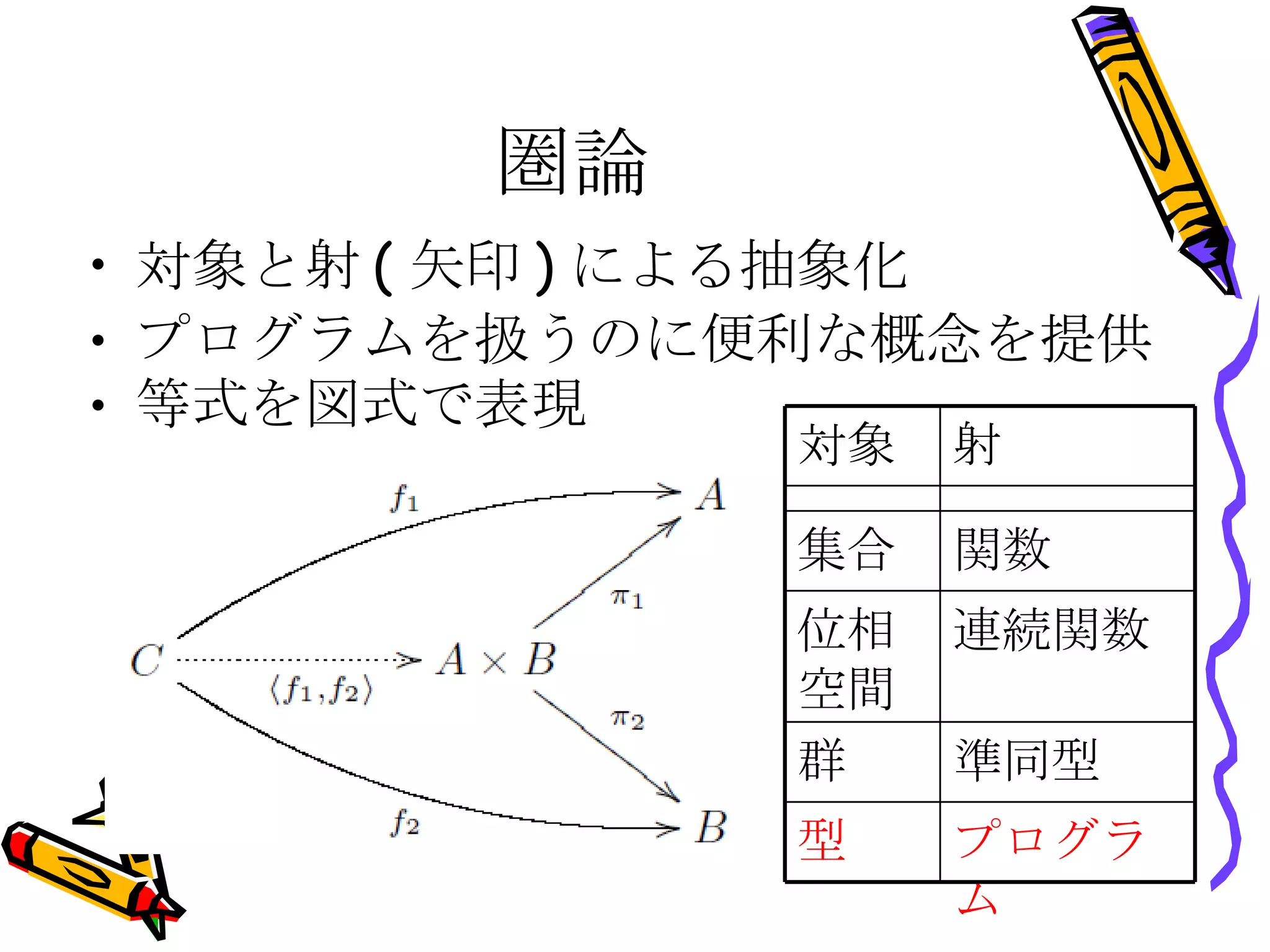
22. 圏論 対象と射 ( 矢印 ) による抽象化 プログラムを扱うのに便利な概念を提供 等式を図式で表現 連続関数 位相空間 準同型 群 関数 集合 プログラム 型 射 対象

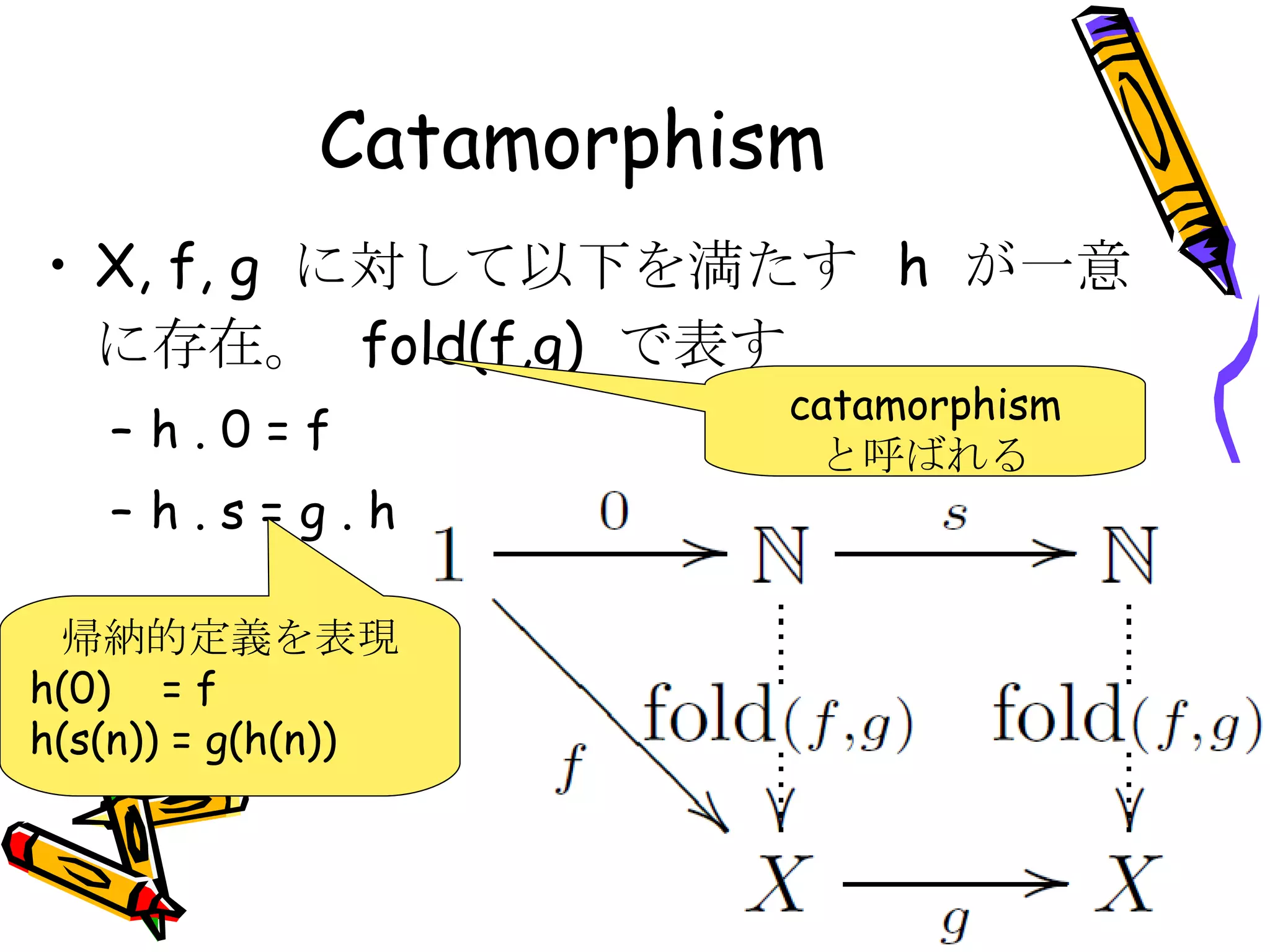
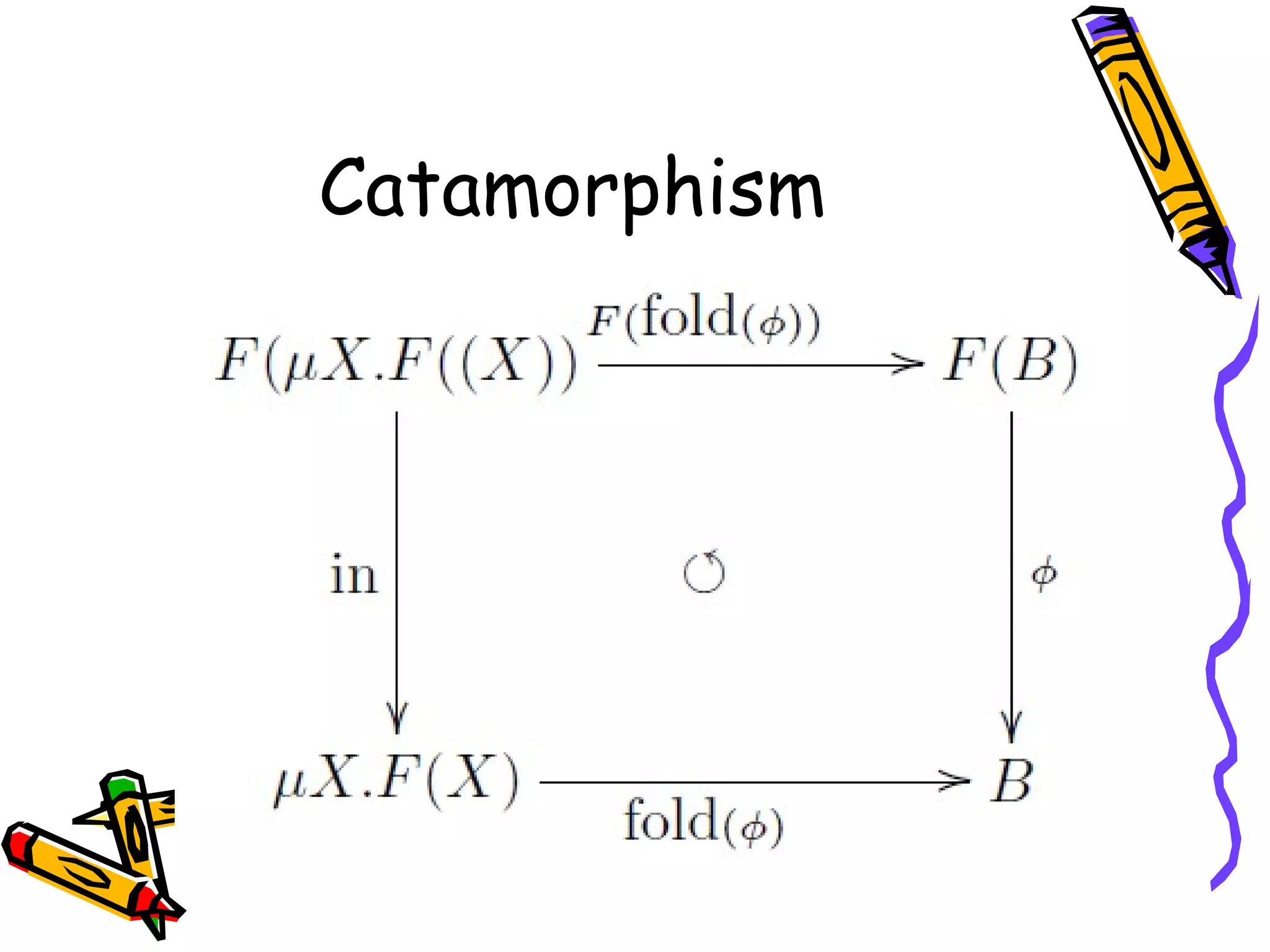
23. Catamorphism X, f, g に対して以下を満たす h が一意に存在。 fold(f,g) で表す h . 0 = f h . s = g . h 帰納的定義を表現 h(0) = f h(s(n)) = g(h(n)) catamorphism と呼ばれる

24. Catamorphism の例 2 倍する関数 double : N -> N double(0) = 0 double(s(n)) = s(s(double(n)) fold で表現 double = fold(0, s.s)

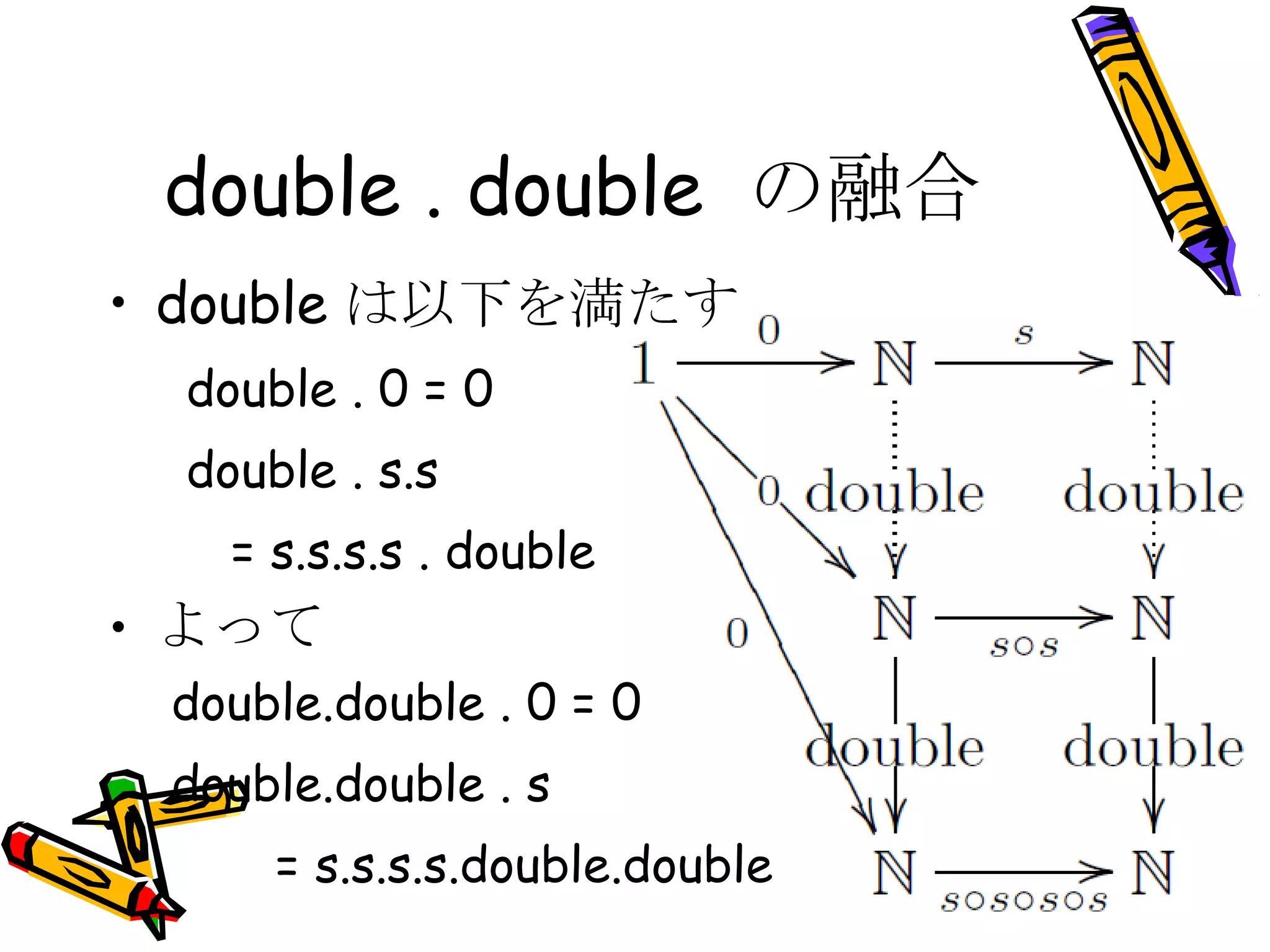
25. double . double の融合 double は以下を満たす double . 0 = 0 double . s.s = s.s.s.s . double よって double.double . 0 = 0 double.double . s = s.s.s.s.double.double

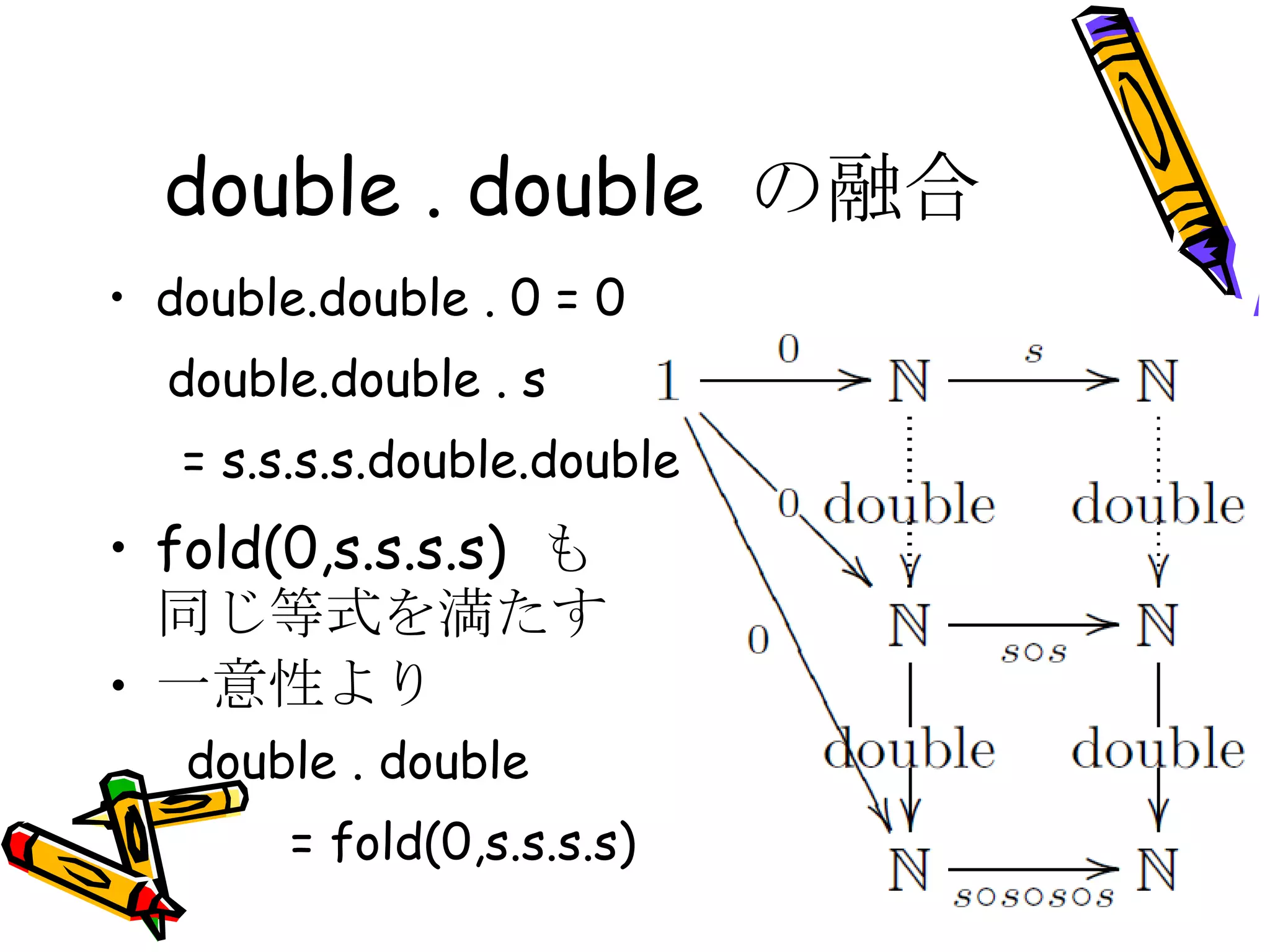
26. double . double の融合 double.double . 0 = 0 double.double . s = s.s.s.s.double.double fold(0,s.s.s.s) も 同じ等式を満たす 一意性より double . double = fold(0,s.s.s.s)

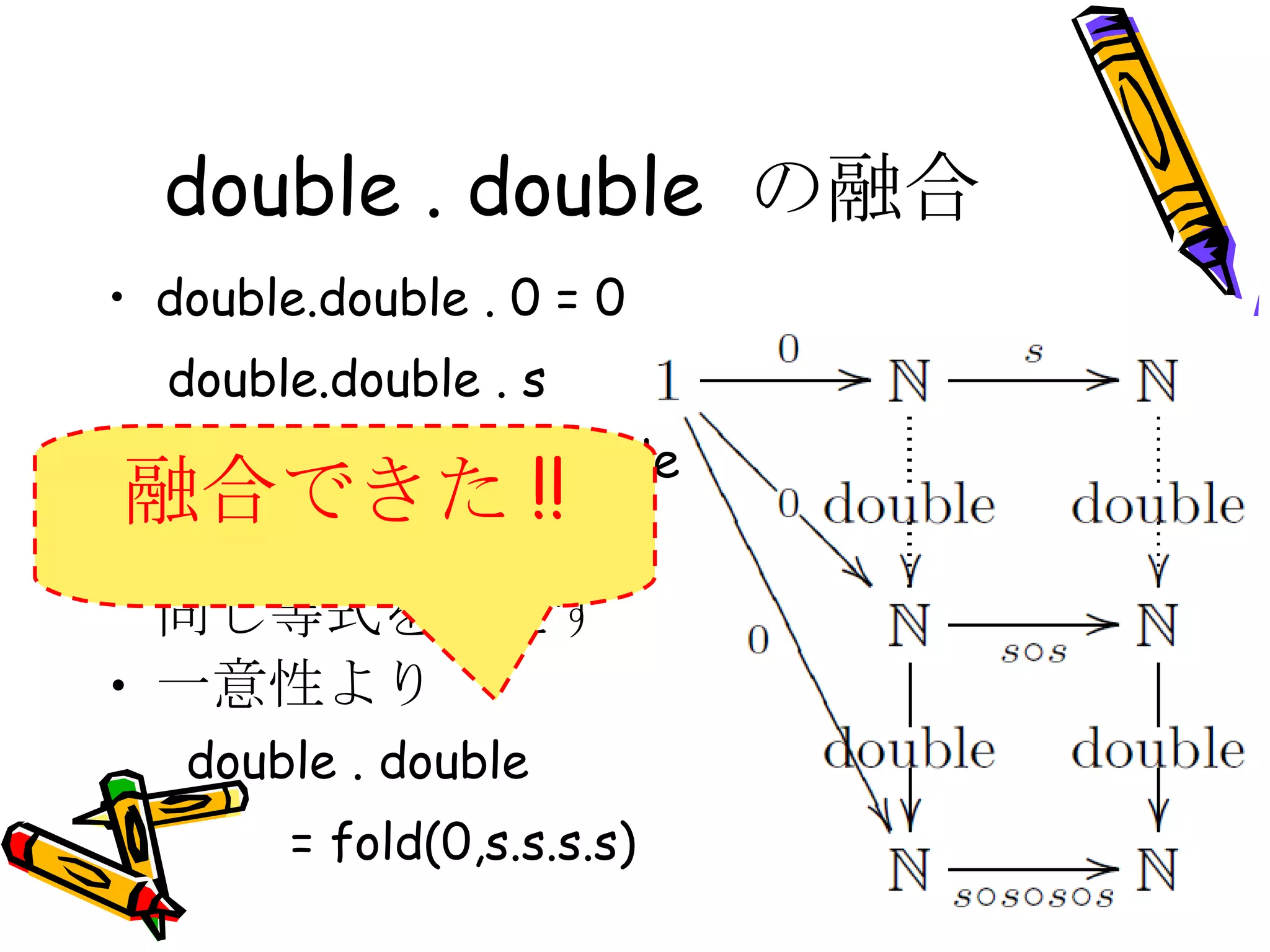
27. double . double の融合 double.double . 0 = 0 double.double . s = s.s.s.s.double.double fold(0,s.s.s.s) も 同じ等式を満たす 一意性より double . double = fold(0,s.s.s.s) 融合できた !!

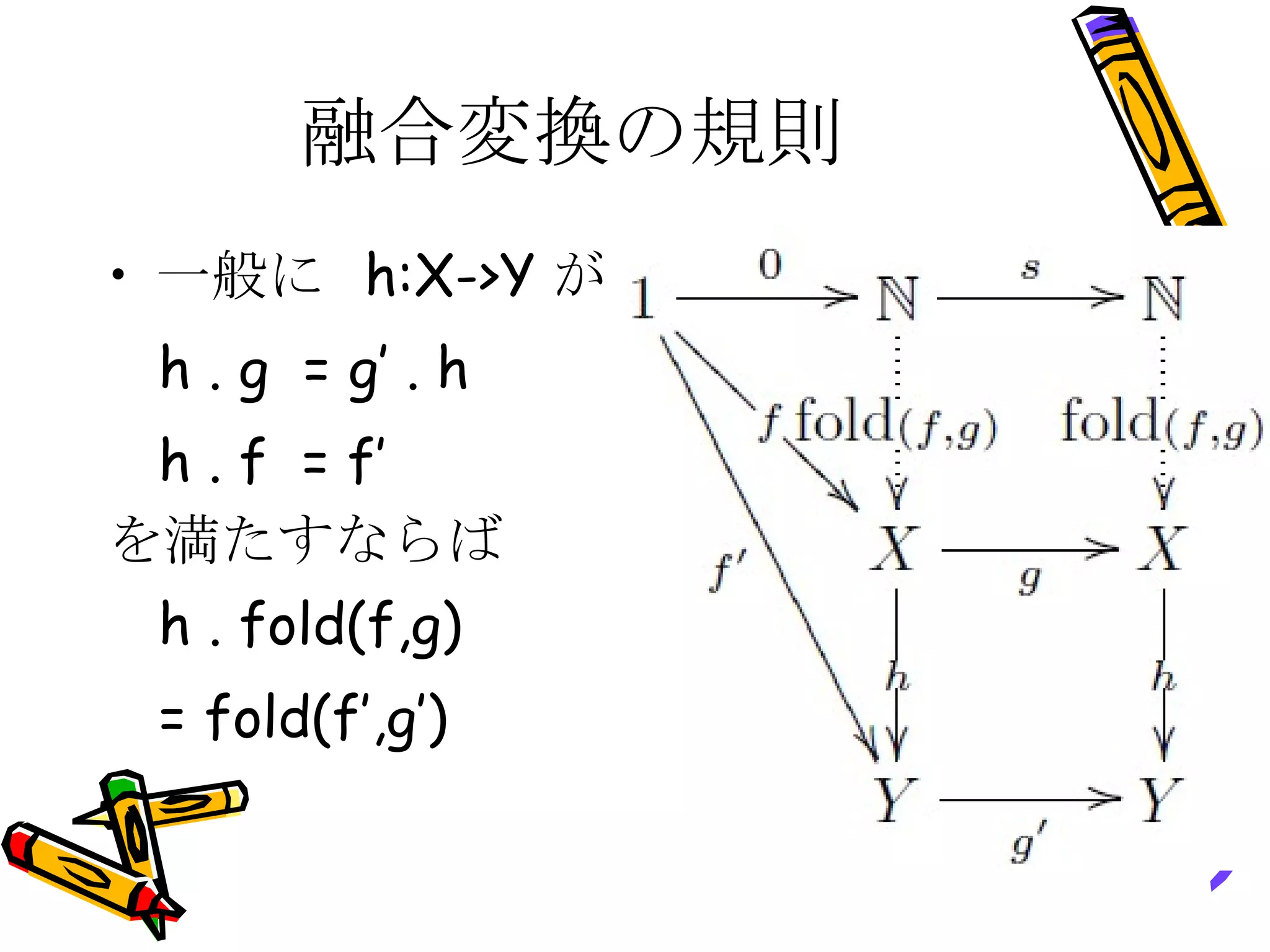
28. 融合変換の規則 一般に h:X->Y が h . g = g’ . h h . f = f’ を満たすならば h . fold(f,g) = fold(f’,g’)

29. データ型の一般化 以上の話は帰納的(inductive)なデータ型一般に対して、一般化出来る リスト, 木, etc.

30. 融合の難しさ h . fold(f,g) = fold(f’,g’) 関数は fold(f,g) の形をしていないかも f’, g’ をどう発見するか ? 対策 Shortcut 融合変換 関数を融合しやすい形で定義しておく Warm Fusion 一般の再帰的定義から fold/build を導出

31. 融合変換の実装例(1) Haskellの処理系GHC 標準関数は short-cut 融合変換可能な形で定義されている short-cut 融合変換の書き換え規則をプラグマとして定義 10クイーンで43%, 大規模ベンチマークで平均3%の実行時間改善

32. 融合変換の実装例(2) 尾上 能之 『融合変換による関数プログラムの最適化』 [Onoue’99] 再帰的定義から Hylomorphism という形式を導出し、 Hylo-Cata fusion という規則によって融合を行う GHC に実装

33. 私の研究

34. 尾上らの手法の問題 Hylo-Cata のみを扱いその双対の Hylo-Ana を扱っていない Hylomorphism と酸性雨定理を組み合わせることの正当性の問題

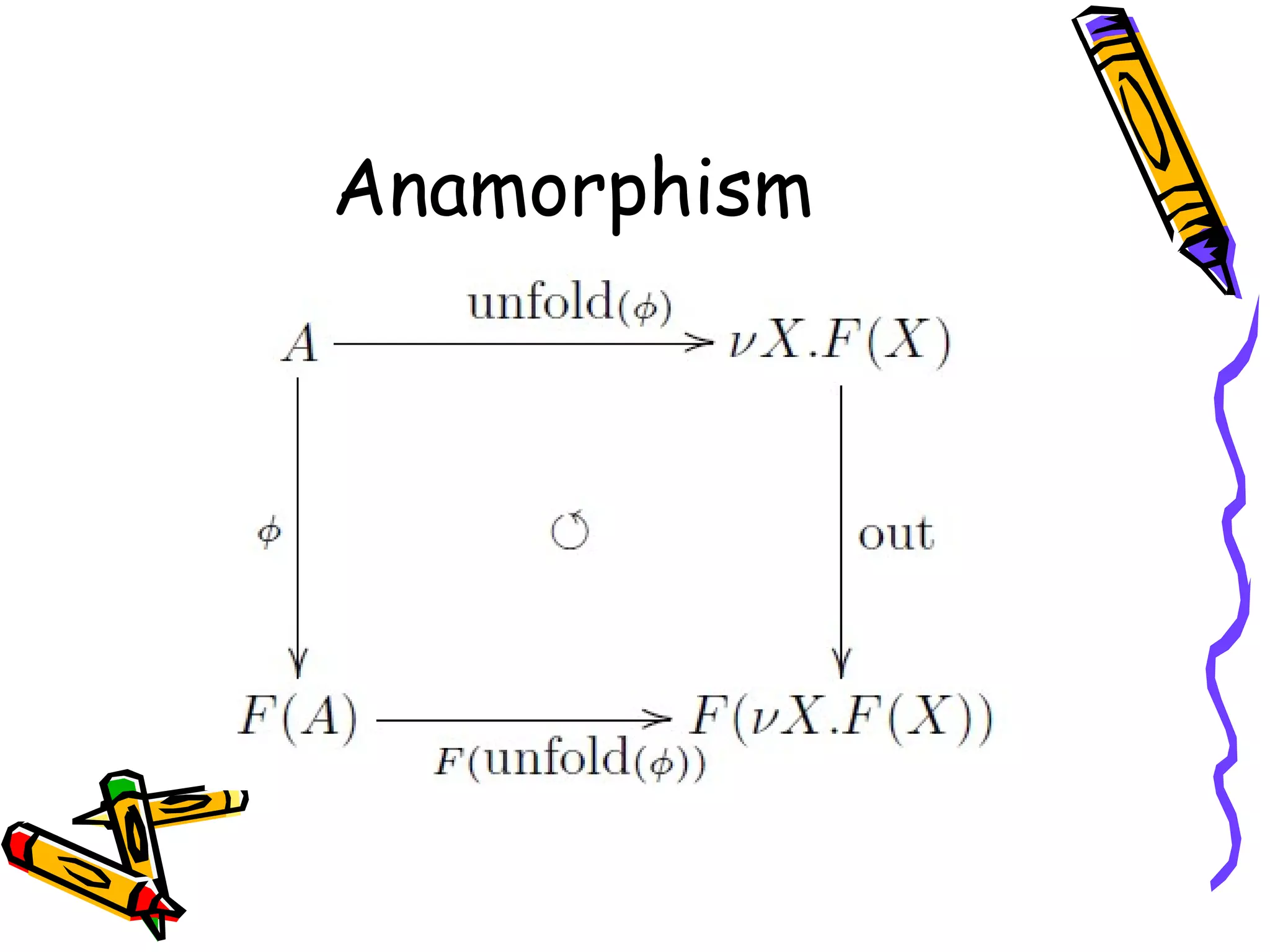
35. 正当性の問題 Hylomorphism と Free Theorems を使用 Hylomorphism には Inductive なデータ型と Coinductive なデータ型の一致が必要 μX. F(X) = νX. F(X) …(A) Free Theorems はパラメトリシティに依存 (A) とパラメトリシティは厳密には 矛盾 !!

36. Catamorphism

37. Anamorphism

38. Hylomorphism Coinduction (Anamorphism) より unfold(φ): A -> νX. F(X) Induction (Catamorphism) より fold(ψ) : μX. F(X) -> B νX. F(X) = μX. F(X) のとき、 これらを結合して A -> B が得られる これが Hylomorphism

39. パラメトリシティ 型を関係として解釈して性質を証明 具体的な型は「等しい」という関係で解釈 型変数は任意の関係で解釈

40. パラメトリシティ(2) 例 ) length : ∀A. List(A) -> N ∀ A,A’,R⊆AxA’. (xs,ys)∈List(R) ⇒ length xs = length ys xRy iff y = f(x) とおくと、 ∀ A,A’,f: A->A’. ys = List(f)(xs) ⇒ length xs = length ys length xs = length (map f xs)

41. なぜ矛盾するか ラムダ計算に基づく体系では以下が同値 Inductive なデータ型と Coinductive なデータ型が一致 すべての型 A に不動点コンビネータ fixA: (A -> A) -> A が存在

42. なぜ矛盾するか (2) ラムダ計算 = Cartesian Closed Category パラメトリシティ の元では、直和 A+B を ∀C. (A->C) -> (B->C) -> C で表現可能 Cartesian Closed Category では 直和と不動点コンビネータは矛盾 正確には退化したモデルしか存在しない

43. 何が困るのか 正当性は微妙なのは気持ち悪い 本来成り立っていない等式に基づいた最適化が行われてしまう可能性 アドホックに正当性を保障することは可能だが、一般的な保障が欲しい

44. アプローチ 形式的な意味論を用いた正当化 今考えているアイディア Moral equality [Danielsson’06] の利用? 途中の過程では弱い等号を用いる

45. 目的 正当性を理論的に保障 融合変換をより安全に広い範囲で使用可能に 安全で強力な最適化技術の実現 信頼性と性能の両立を

46. 目的(2) また、その過程で、融合変換についてのよりよい理解が得られるのではないか? それによって、より高度な融合変換を

47. 詳しくは現在研究中

48. まとめ プログラム変換の一つとしての融合変換 融合変換の簡単な例と理論 私のアプローチ