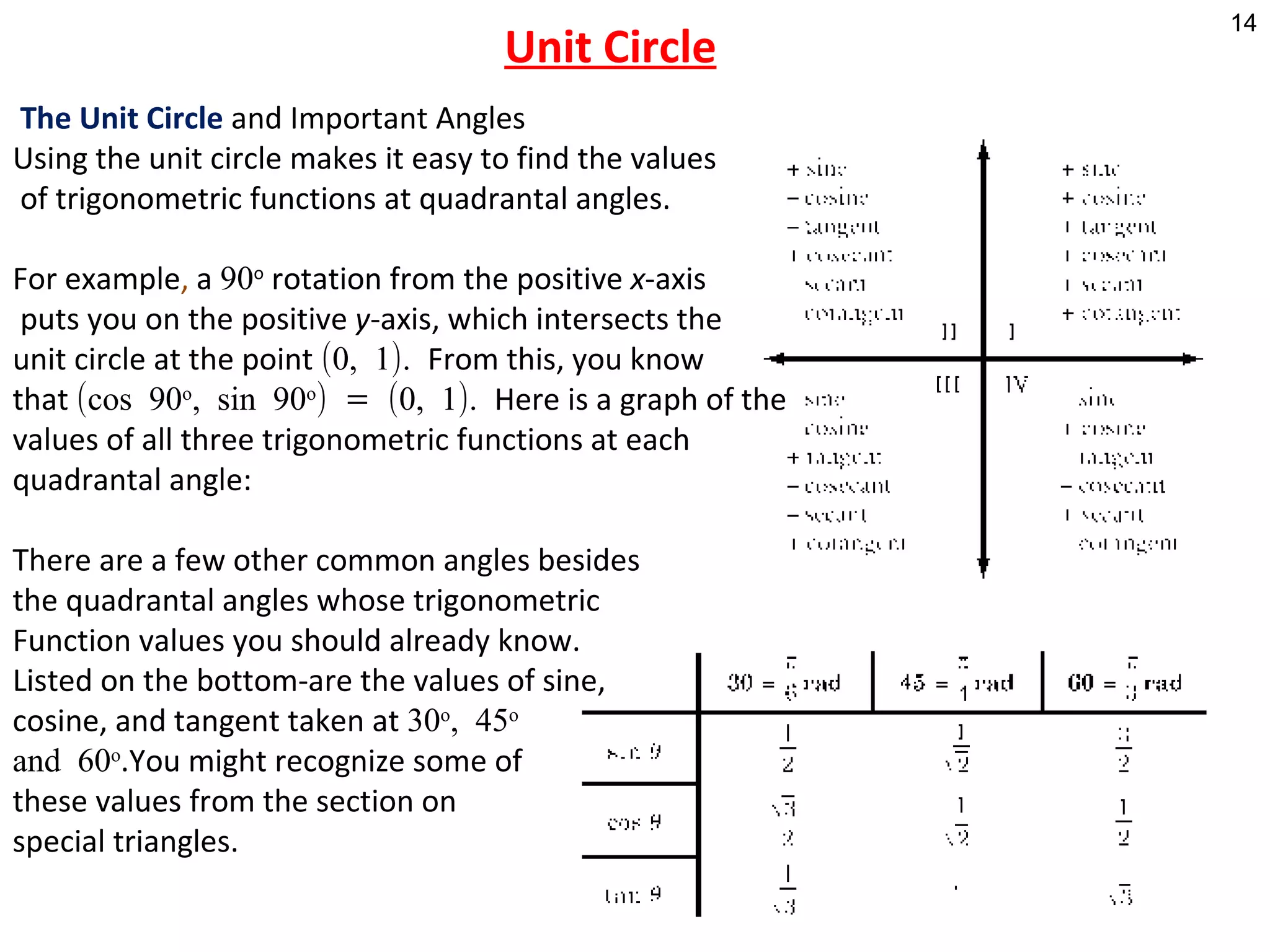
The document discusses basic trigonometric functions and their use in solving right triangles. It introduces the trig functions of sine, cosine, and tangent and defines them relative to angles and sides of a right triangle. It also covers solving right triangles when given one angle and one side or when given two sides, using trig identities and the Pythagorean theorem.











![Trigonometric Identities A trigonometric identity is an equation involving trigonometric functions that holds true for all angles. These identities are commonly called Pythagorean identities, because they come from the Pythagorean theorem. tan = Sin / Cos sin 2 + cos 2 = 1 You will have to by asking you to simplify a complex expression. Answering these questions has more to do with memorizing the identities and being good with algebraic substitution than it does with the theoretical concepts of trigonometry. For example: What is (cos tan ) / (sin – cos 2 )? To solve a problem like this, use the trigonometric identities to simplify the trigonometric into sines and cosines. After you have simplified the expression using the identities, it is quite likely that the expressions will simplify further due to the canceling of terms. The simplification of the expression in the example question proceeds as follows: (Cos X tan )/Sin – Cos 2 = [(Cos X Sin ) /Sin X Cos ] - Cos 2 = 1-Cos 2 = Sin 2 Simplifying the mess given to you by the problem, you get sin 2 .](https://image.slidesharecdn.com/mathtest05-1227672366243324-9/75/slide-12-2048.jpg)