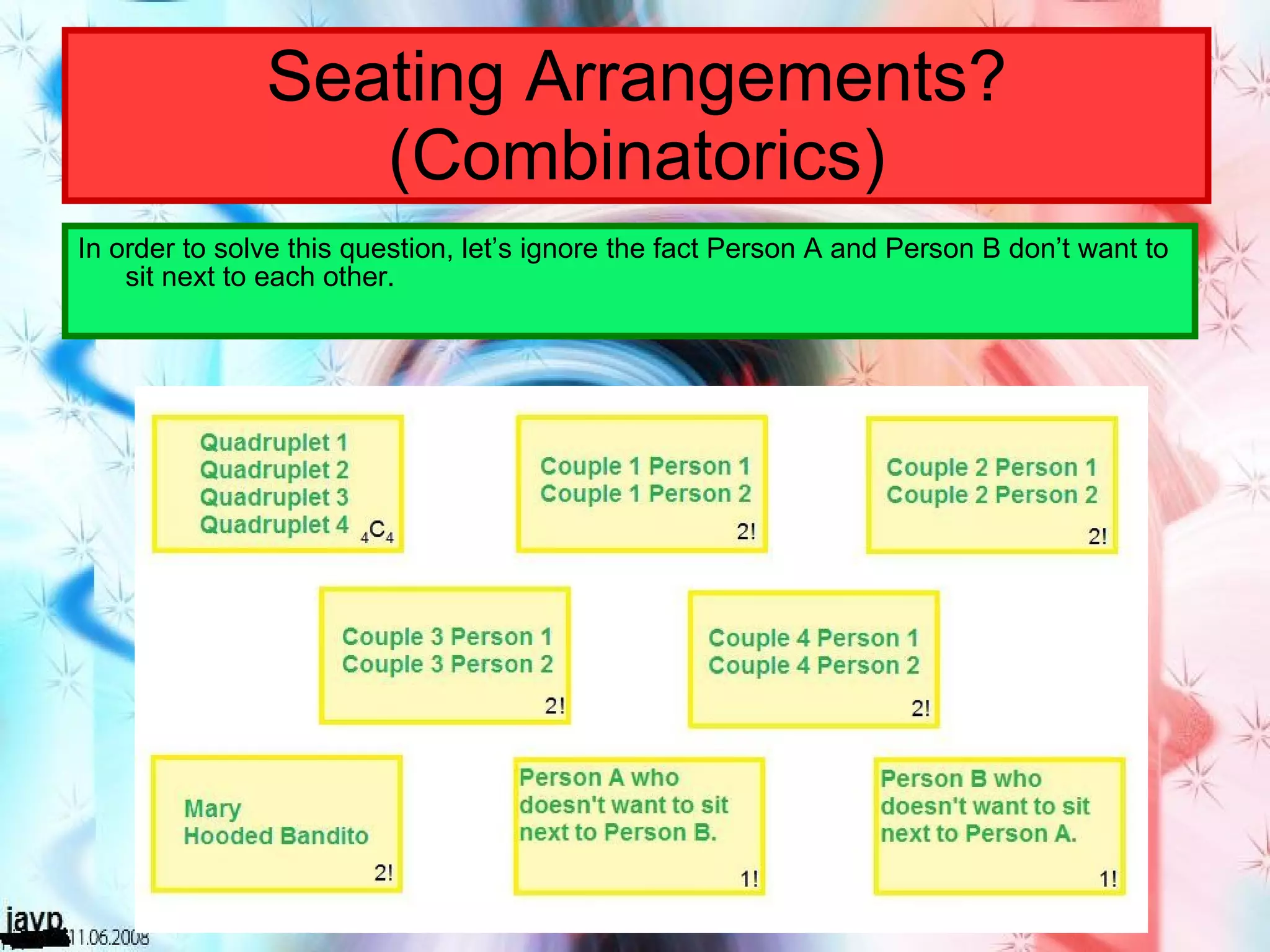
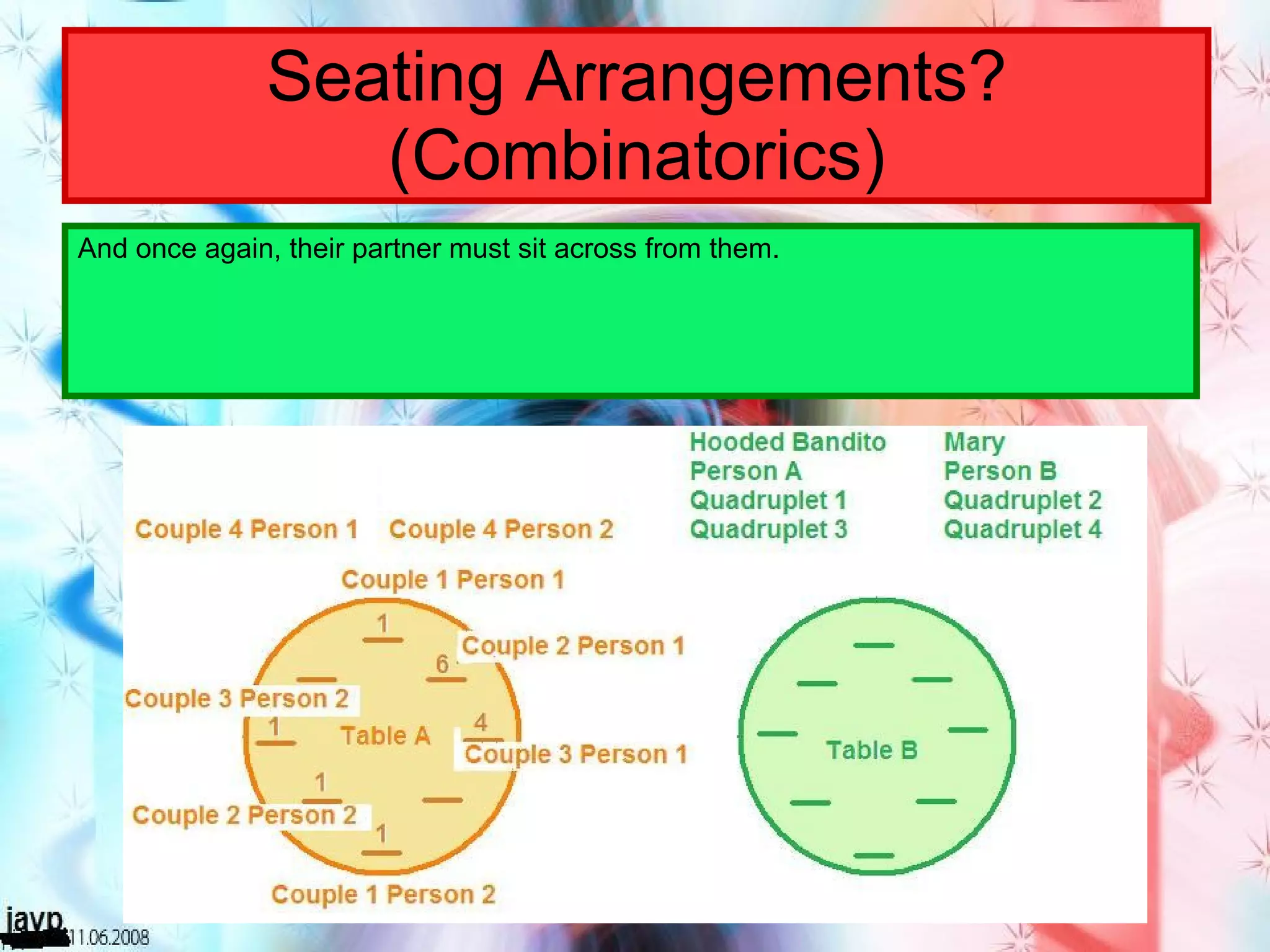
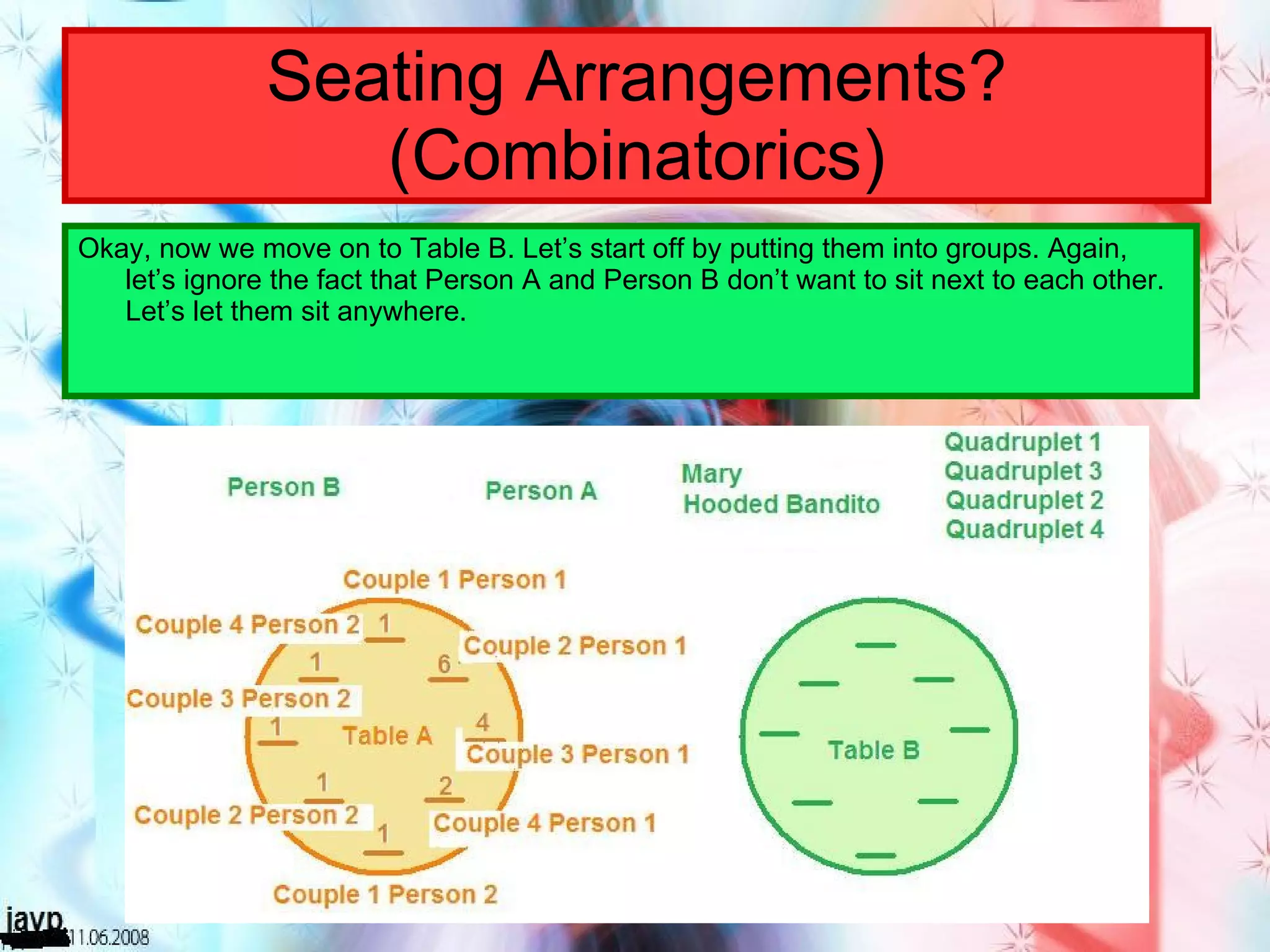
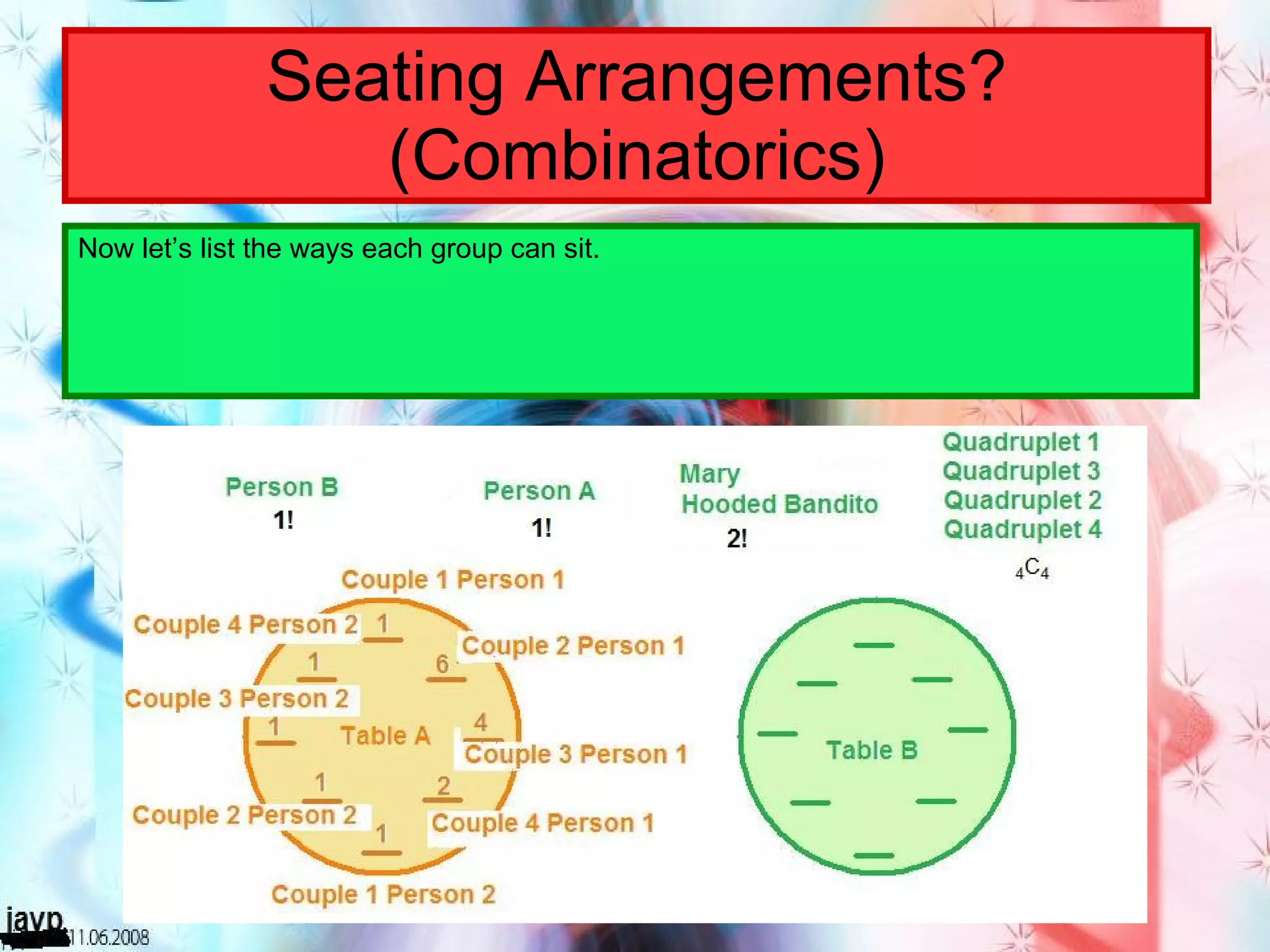
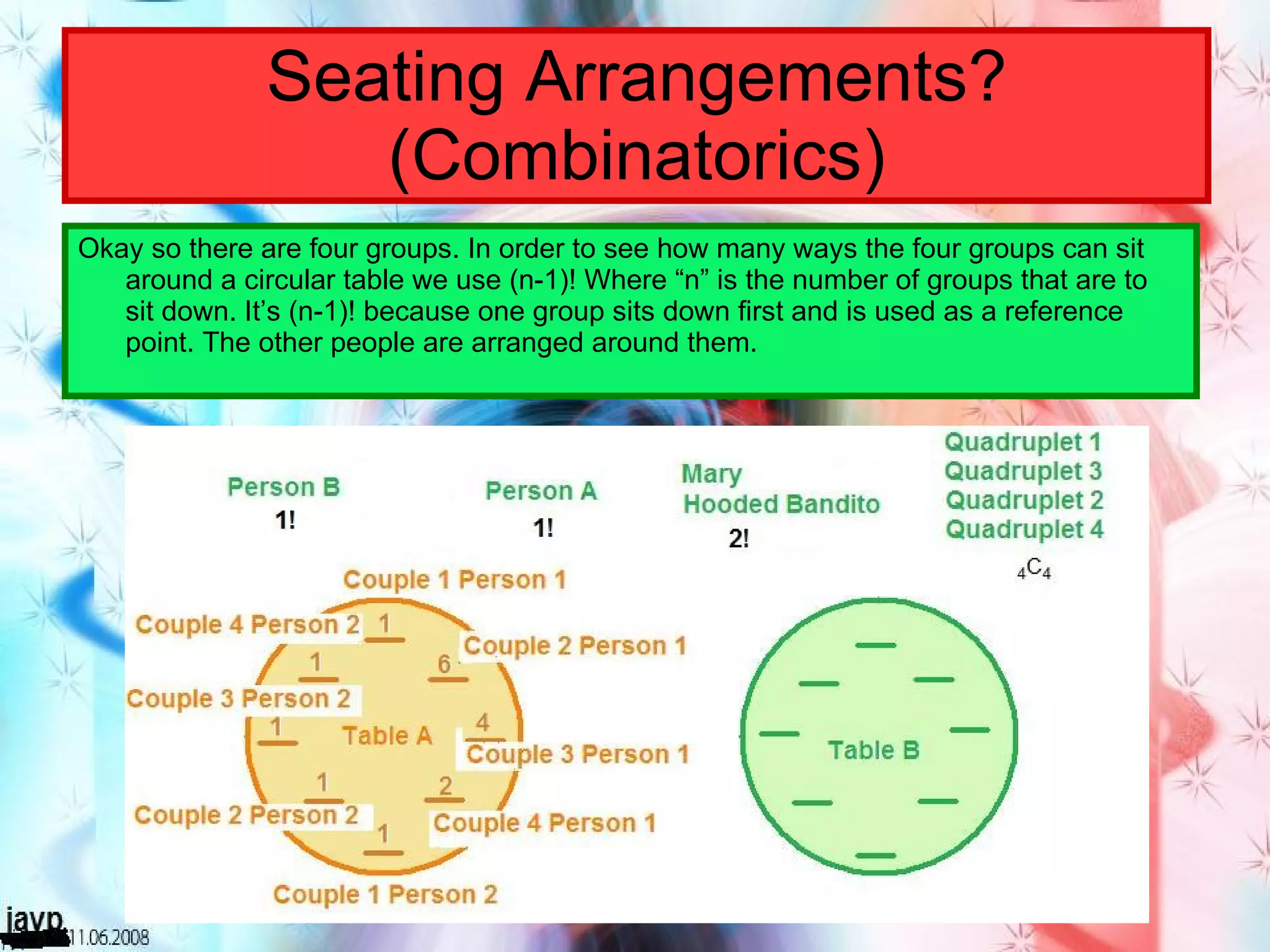
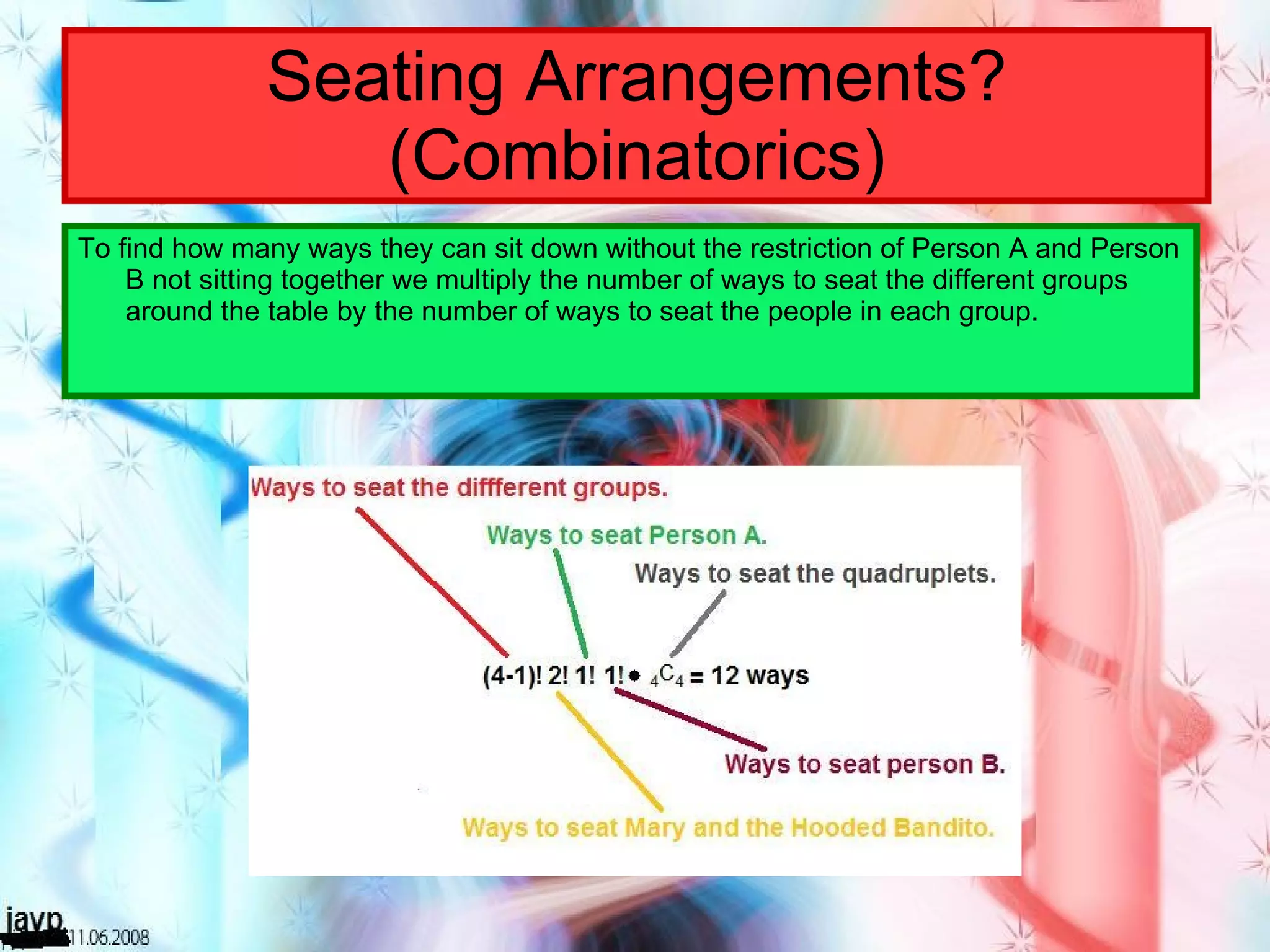
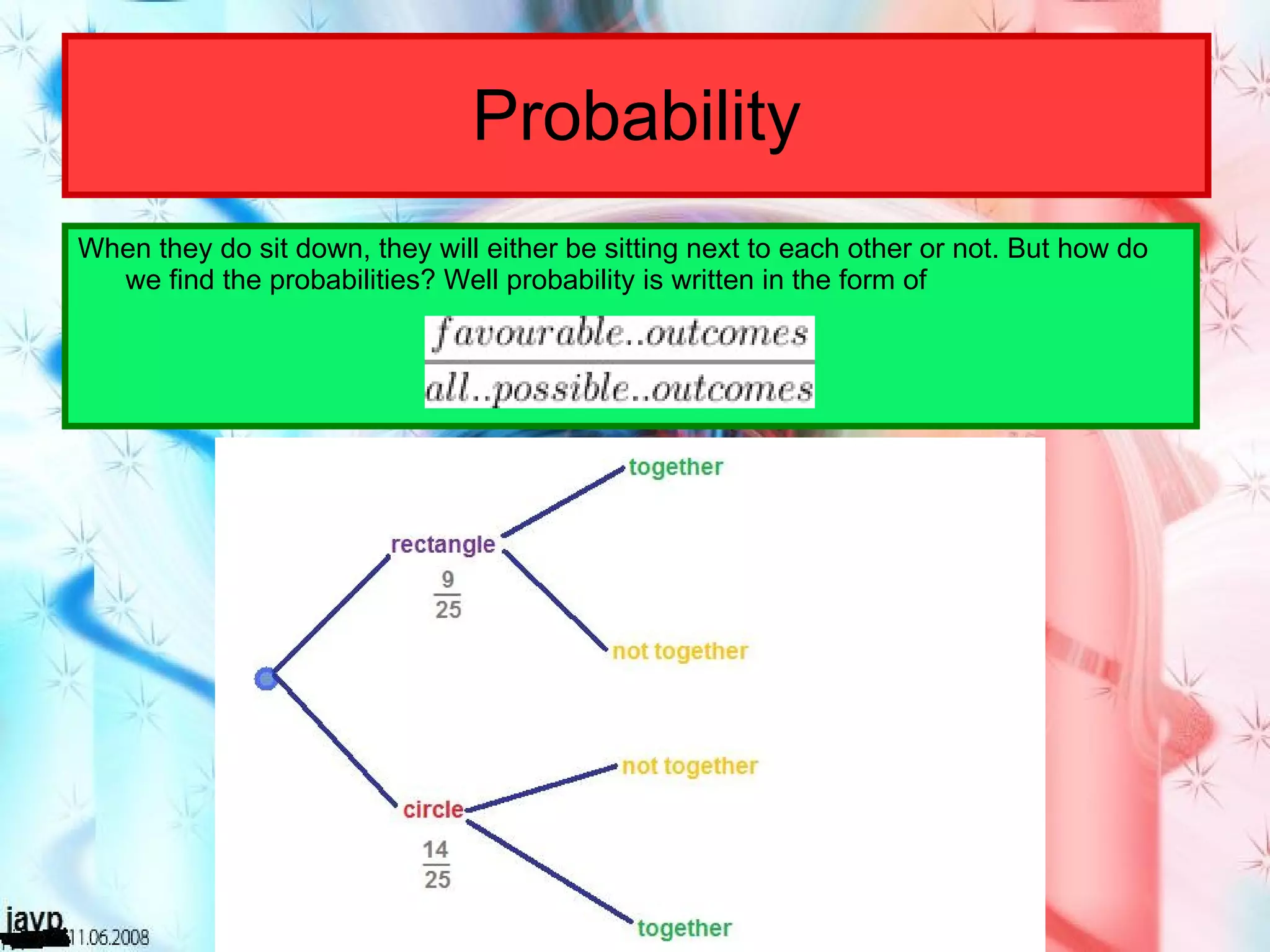
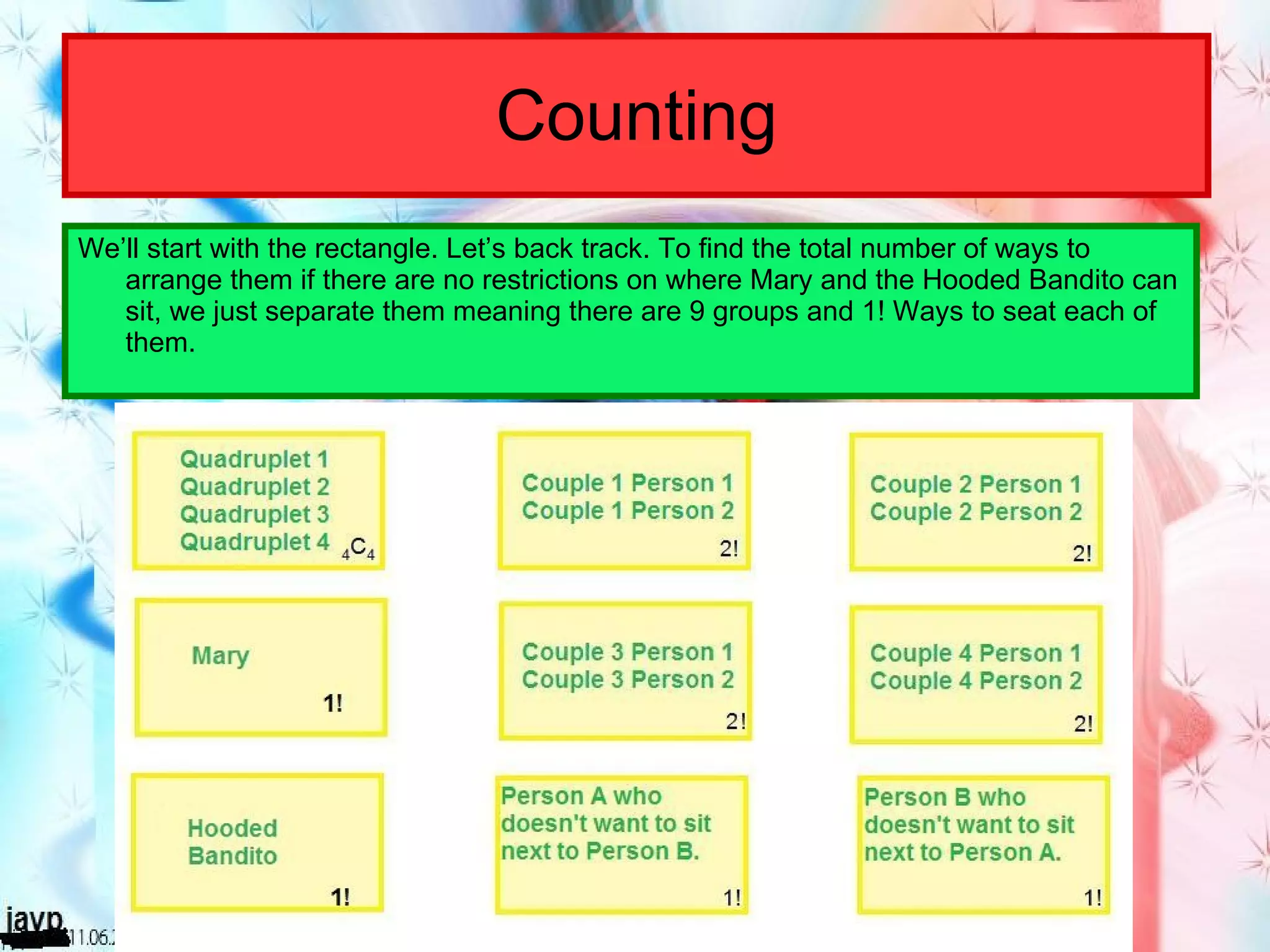
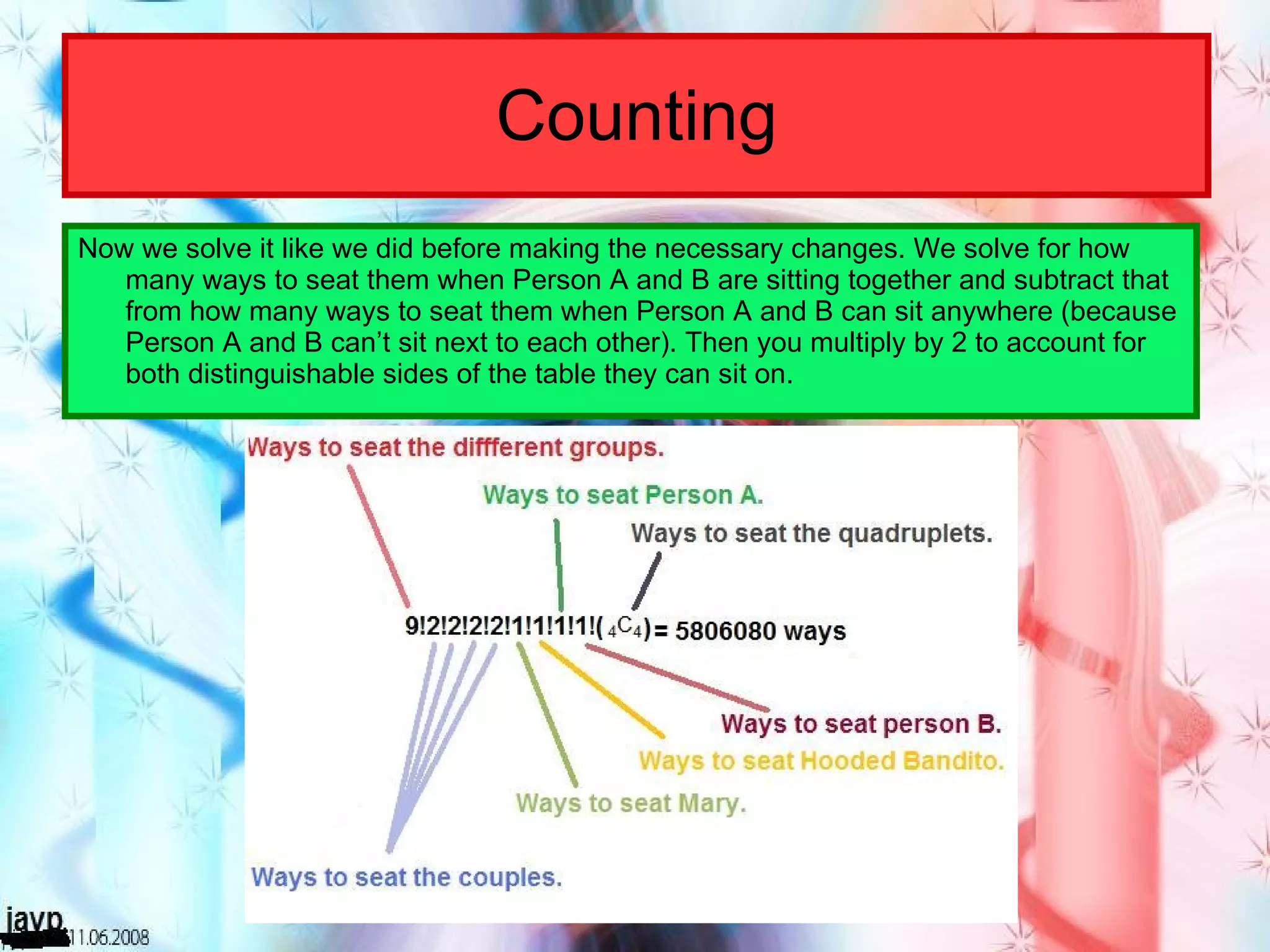
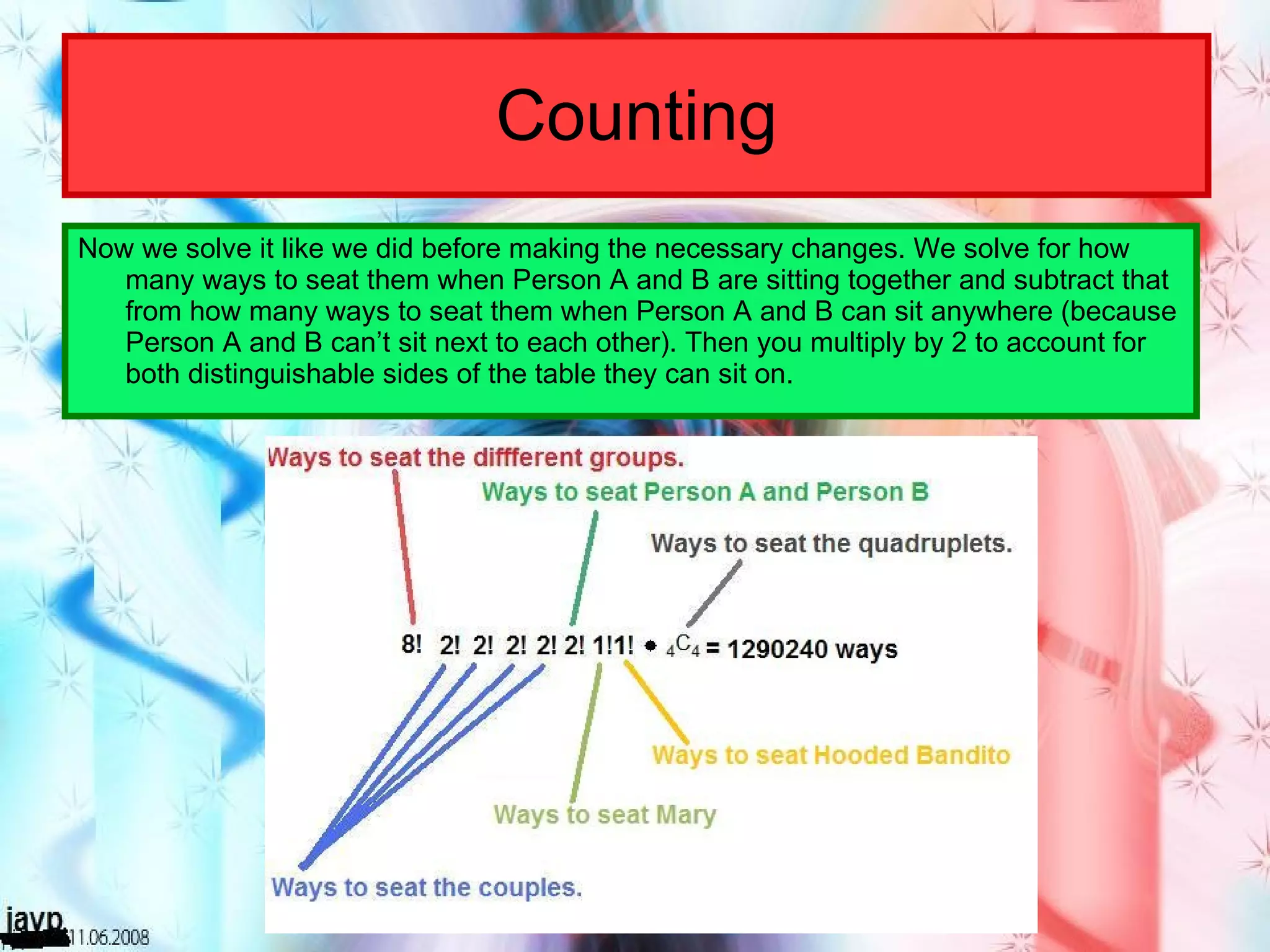
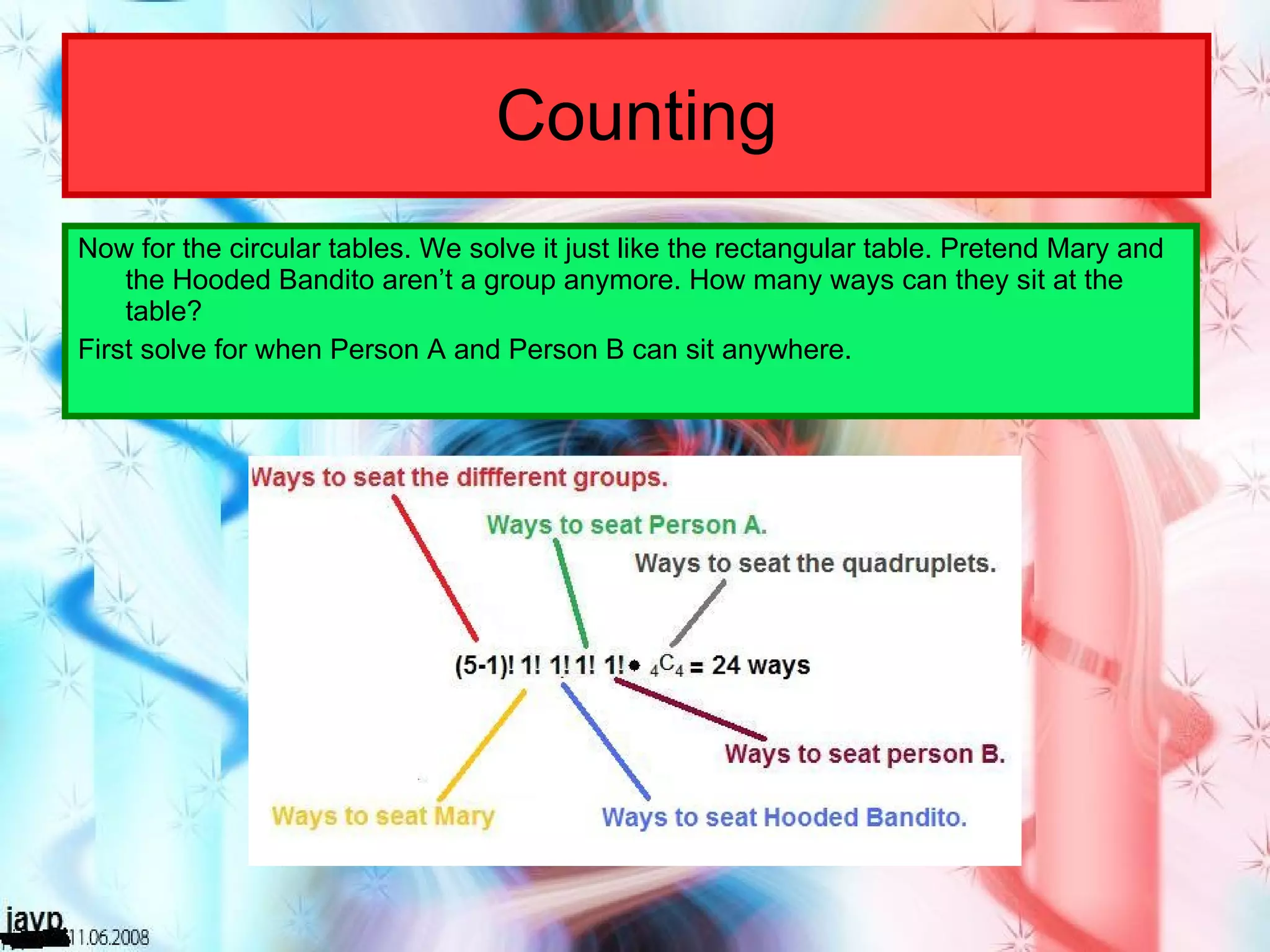
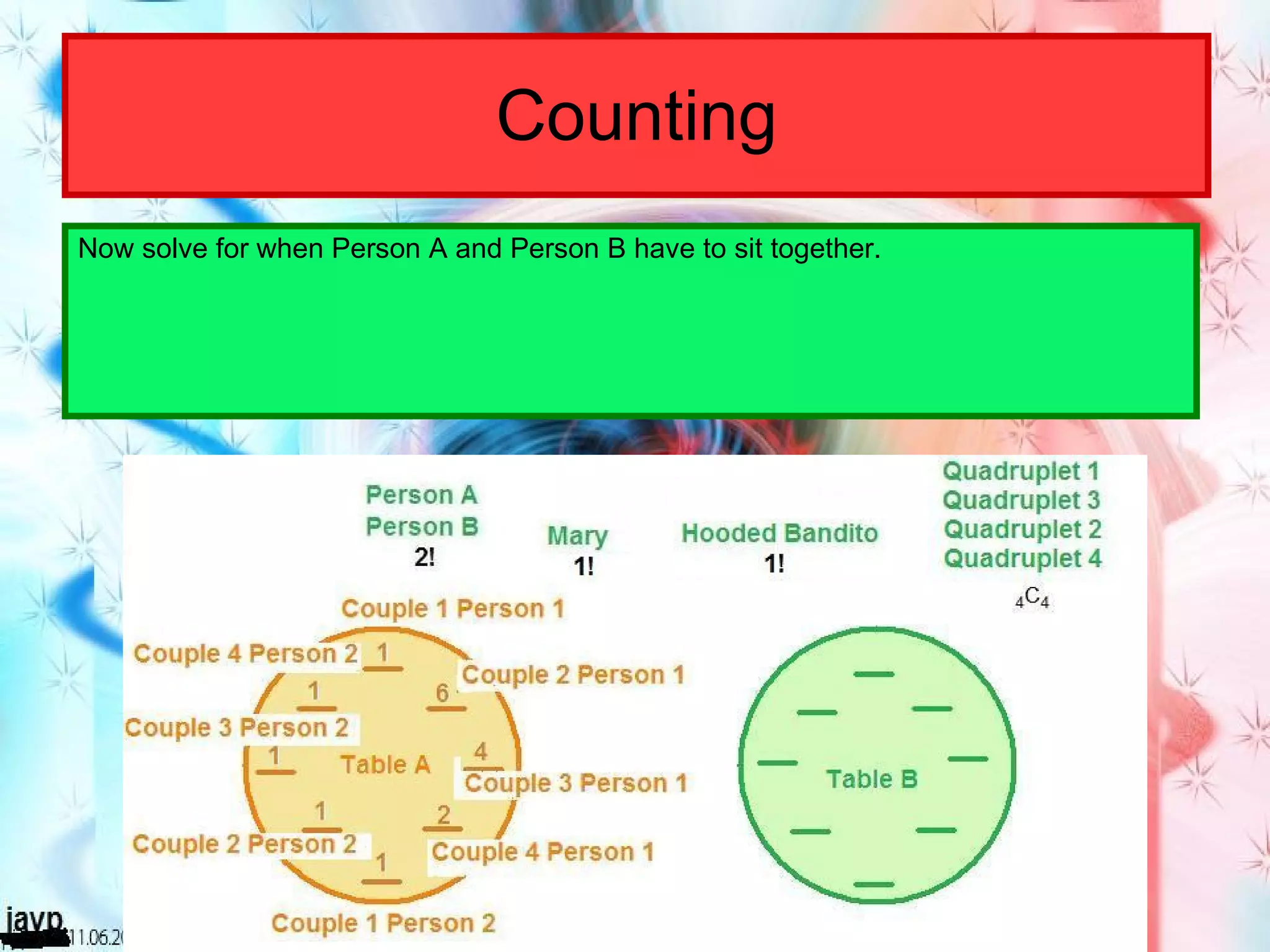
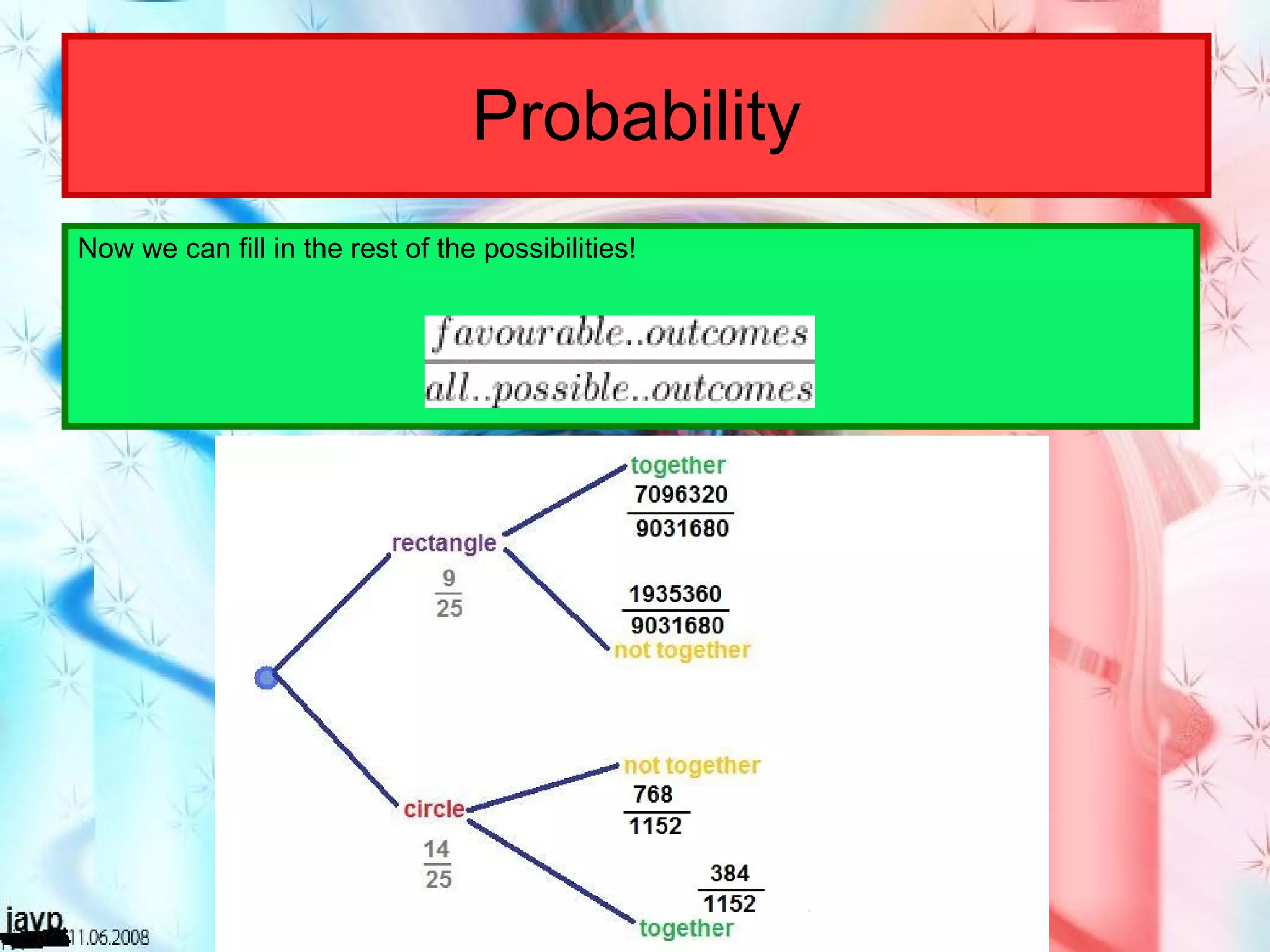
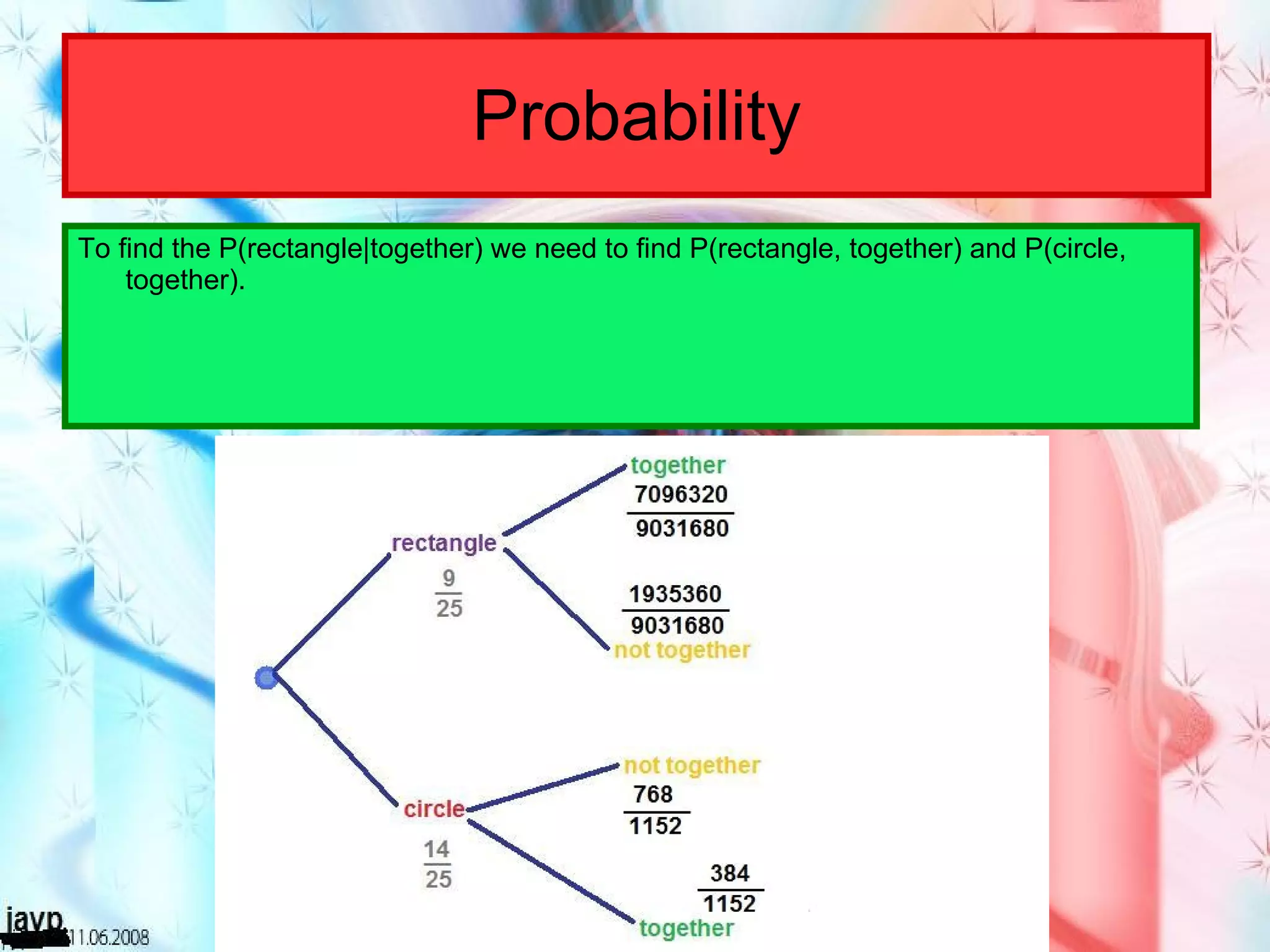
There are multiple questions about calculating the number of possible seating arrangements given various conditions about groups of people sitting at tables. The first question involves people sitting at a rectangular table and has conditions about couples and others. The second question adds two circular tables and additional conditions. The third question asks for the probability that two people are sitting at a rectangular table given they are sitting together. It requires calculating total arrangements and matching scenarios to use the probability formula.

1. Question 3 How many ways can Mary sit?

2. Question Agent Double OH 3.14 has arrived in the café. She wants to sit beside the Hooded Bandito. How many ways can she sit next to the Hooded Bandito if the following details apply: There are 4 couples. There is 1 set of quadruplets that all look the same. There are 2 other people who refuse to sit next to each other. Mary and the Hooded Bandito must sit together. The quadruplets must sit together. Each couple must be sitting next to their partner. The table is rectangular, but they all sit on either of the longer sides. The two sides are distinguishable.

3. Question What about if those same conditions were there but: There are two circular tables which seat 8 people each instead of one rectangular table: Table A and Table B. All the couples are at one table. The couples must be sitting across from their partners. One of the people who refuses to sit next to a second person is seated first at the other table.

4. Question One last question. If there are 25 tables in all (7 pairs of circular tables, the rest are rectangular) and Mary and the Hooded Bandito didn’t have to sit next to each other, what is the probability that they are sitting at a rectangular table given the fact that they are sitting next to each other?

5. DO NOT MOVE ON UNTIL YOU HAVE ANSWERED THE QUESTION OR YOU NEED HELP!

6. Things You Should Know Ooooh. There’s a lot to this question. It covers Combinatorics and Probability. Let’s start with the beginning. How many ways can she sit next to the Hooded Bandito if the following details apply: There are 4 couples. There is 1 set of quadruplets that all look the same. There are 2 other people who refuse to sit next to each other. Mary and the Hooded Bandito must sit together. The quadruplets must sit together. Each couple must be sitting next to their partner. The table is rectangular, but they all sit on either of the longer sides.

7. Seating Arrangements? (Combinatorics) First off, let’s put the people in groups.

8. Seating Arrangements? (Combinatorics) Now let’s put in the ways you can seat each group. * For the quadruplets, it will be 4 C 4 because they all look the same. They are indistinguishable objects. 4 C 4 2! 2! 2! 2! 2! 1! 1!

9. Seating Arrangements? (Combinatorics) In order to solve this question, let’s ignore the fact Person A and Person B don’t want to sit next to each other.

10. Seating Arrangements? (Combinatorics) Now let’s write out the equation. The number of ways we found here covers all the possibilities from the question except for the part where Person A and Person B don’t want to sit next to each other. In this case, Person A and Person B can sit anywhere.

11. Seating Arrangements? (Combinatorics) In order to solve for the fact that Person A and Person B refuse to sit next to each other, let’s look at the possibilities where they do sit together. This means we have to put them in a group. There are 2! Ways they can sit next to each other.

12. Seating Arrangements? (Combinatorics) In order to solve for the fact that Person A and Person B refuse to sit next to each other, let’s look at the possibilities where they do sit together. This means we have to put them in a group. There are 2! Ways they can sit next to each other. This makes 7 groups now instead of 8.

13. Seating Arrangements? (Combinatorics) Now let’s write out the equation. The number of ways we found here covers all the possibilities from the question except Person A and Person B are sitting next to each other.

14. Seating Arrangements? (Combinatorics) We’re not there yet! Remember they are sitting at a rectangular table. A rectangular table has two long sides. The question states they can sit on either side as long as they are all sitting on the same side. This means that we have to multiply to answer by 2. So there are 967680 x 2 ways or 1935360 ways for them to sit.

15. Sweet! Let’s Move On! Haah. Ok, next question. What about if those same conditions were there but: There are two circular tables which seat 8 people each instead of one rectangular table: Table A and Table B. These tables are distinguishable. All the couples are at one table. The couples must be sitting across from their partners.

16. Seating Arrangements? (Combinatorics) Alright, so now we have to deal with two tables that are circular. All the couples are at one table and everyone else is at the other table. Let’s draw that out shall we?

17. Seating Arrangements? (Combinatorics) So let’s start with Table A. The first thing we do is set up a reference point. Everyone will be seated around that person. It could really be anybody because when you look at it, you can’t tell who sat down first and some seating arrangements will look the same as others. For now, we’ll pick Couple 1 Person 1 .

18. Seating Arrangements? (Combinatorics) Now that we’ve sat that person down, we mark that there was only 1 choice for that seat: that person. The other rule is that the couples must be sitting across from their partner so we only have 1 choice for the seat across from that person: the reference person’s partner.

19. Seating Arrangements? (Combinatorics) Now any one of the 6 remaining people could be sitting next to Couple 1 Person 1 meaning there are 6 choices for that seat.

20. Seating Arrangements? (Combinatorics) There is only one choice for the seat across this person as well: that person’s partner.

21. Seating Arrangements? (Combinatorics) Now there’s only 4 people left to sit next to that person.

22. Seating Arrangements? (Combinatorics) And once again, their partner must sit across from them.

23. Seating Arrangements? (Combinatorics) Now there are only two choices left for the second last seat and their partner must be sitting across from them. To find out how many ways to seat the people here, we multiply all the numbers we have just found. (1)(6)(4)(2)(1)(1)(1)(1)= 48 ways

24. Seating Arrangements? (Combinatorics) Okay, now we move on to Table B. Let’s start off by putting them into groups. Again, let’s ignore the fact that Person A and Person B don’t want to sit next to each other. Let’s let them sit anywhere.

25. Seating Arrangements? (Combinatorics) Now let’s list the ways each group can sit.

26. Seating Arrangements? (Combinatorics) Okay so there are four groups. In order to see how many ways the four groups can sit around a circular table we use (n-1)! Where “n” is the number of groups that are to sit down. It’s (n-1)! because one group sits down first and is used as a reference point. The other people are arranged around them.

27. Seating Arrangements? (Combinatorics) To find how many ways they can sit down without the restriction of Person A and Person B not sitting together we multiply the number of ways to seat the different groups around the table by the number of ways to seat the people in each group.

28. Seating Arrangements? (Combinatorics) To find how many ways they can sit down with the restriction of Person A and Person B not sitting together we should find out how many ways they can sit together if they do sit together. This means there will be 3 groups now instead of 4 and there are 2! ways to seat the new group.

29. Seating Arrangements? (Combinatorics) Let’s figure out how many ways that is.

30. Seating Arrangements? (Combinatorics) To find out how many ways to seat them with the restriction that Person A can’t sit next to Person B, we subtract the number of ways they can sit if they sit together from the number of ways they can sit without restrictions.

31. Seating Arrangements? (Combinatorics) So now we know how many ways each table can be seated. To find out how many seating arrangements there are for both tables we multiply the two values we got together. Why? Because if there are “M” ways of doing one thing and “N” ways of doing another, there are “MN” ways of doing both. We also have to multiply that result by two because the two groups could be sitting at the other tables ( Couples could be at Table B instead of A and Others could be at Table A instead of B).

32. Easy Peasy! Next! Haah. Ok, last part. One last question. If there are 25 tables in all (7 pairs of circular tables, the rest are rectangular) and Mary and the Hooded Bandito didn’t have to sit next to each other, what is the probability that they are sitting at a rectangular table given the fact that they are sitting next to each other?

33. Probability Ok this part involves some work. First let’s start off by drawing a tree. When they arrive in the café, they can either sit a rectangular or a circular table. There is a 14/25 chance of them sitting at a circular table. This means that there is a 9/25 chance that they sit at a rectangular table. (In case you’re wondering where the 14 came from, there are 7 pairs of circular tables meaning 14 round tables.)

34. Probability When they do sit down, they will either be sitting next to each other or not. But how do we find the probabilities? Well probability is written in the form of

35. Probability So lets look at what we know: Sitting at a rectangular table together: 1935360 ways Sitting at a circular table together: 384 ways We need to find: Sitting at a rectangular table not together Sitting at a circular table not together Sitting at a rectangular table Sitting at a circular table

36. Counting We’ll start with the rectangle. Let’s back track. To find the total number of ways to arrange them if there are no restrictions on where Mary and the Hooded Bandito can sit, we just separate them meaning there are 9 groups and 1! Ways to seat each of them.

37. Counting Now we solve it like we did before making the necessary changes. We solve for how many ways to seat them when Person A and B are sitting together and subtract that from how many ways to seat them when Person A and B can sit anywhere (because Person A and B can’t sit next to each other). Then you multiply by 2 to account for both distinguishable sides of the table they can sit on.

38. Counting Now we solve it like we did before making the necessary changes. We solve for how many ways to seat them when Person A and B are sitting together and subtract that from how many ways to seat them when Person A and B can sit anywhere (because Person A and B can’t sit next to each other). Then you multiply by 2 to account for both distinguishable sides of the table they can sit on.

39. Counting Now we solve it like we did before making the necessary changes. We solve for how many ways to seat them when Person A and B are sitting together and subtract that from how many ways to seat them when Person A and B can sit anywhere (because Person A and B can’t sit next to each other). Then you multiply by 2 to account for both distinguishable sides of the table they can sit on. 4515840 x 2 = 9031680 ways

40. Counting To solve for how many ways there are where Mary and the Hooded Bandito don’t sit together, subtract the number of ways there are when they do sit next to each from the number of ways there are when they can sit anywhere.

41. Counting Now for the circular tables. We solve it just like the rectangular table. Pretend Mary and the Hooded Bandito aren’t a group anymore. How many ways can they sit at the table? First solve for when Person A and Person B can sit anywhere.

42. Counting Now for the circular tables. We solve it just like the rectangular table. Pretend Mary and the Hooded Bandito aren’t a group anymore. How many ways can they sit at the table? First solve for when Person A and Person B can sit anywhere.

43. Counting Now solve for when Person A and Person B have to sit together.

44. Counting Now solve for when Person A and Person B have to sit together.

45. Counting Now subtract.

46. Counting And multiply.

47. Counting Now we find how many ways there are for them to sit where Mary and the Hooded Bandito don’t sit together.

48. Probability Now we have everything! Sitting at a rectangular table together: 1935360 ways Sitting at a circular table together: 384 ways Sitting at a rectangular table not together: 7096320 ways Sitting at a circular table not together: 768 ways Sitting at a rectangular table: 9031680 ways Sitting at a circular table: 1152 ways

49. Probability Now we can fill in the rest of the possibilities!

50. Probability To find the P(rectangle|together) we need to find P(rectangle, together) and P(circle, together).

51. Probability To find the P(rectangle|together) we need to find P(rectangle, together) and P(circle, together).

52. Probability Now we plug it in to the equation. P(rectangle|together) ≈60.2434%

53. The probability of them sitting at a rectangular table given the fact that they are sitting next to each other is 60.2434%!

54. Go on and solve the bonus question to move on!