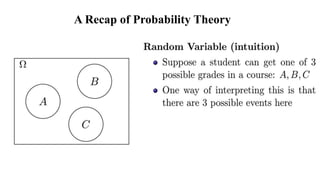
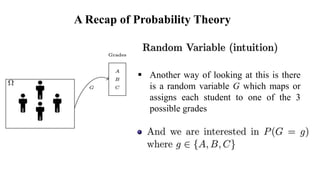
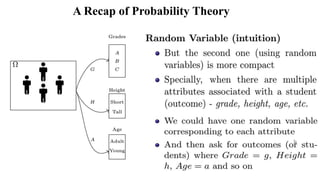
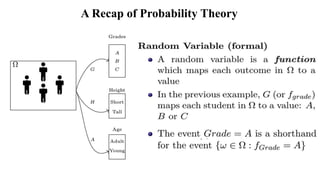
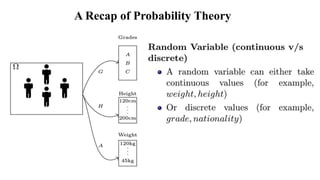
This document provides an overview of probability theory concepts. It defines an experiment as any process of observation or measurement, and a random experiment as one where the exact outcome cannot be predicted but the possible outcomes can be listed. The sample space is the set of all possible outcomes, and a subset is called an event. Probability is defined as the ratio of favorable outcomes to total possible outcomes. Examples are provided of calculating probabilities of events occurring for experiments like rolling dice, tossing coins, and assigning student grades.