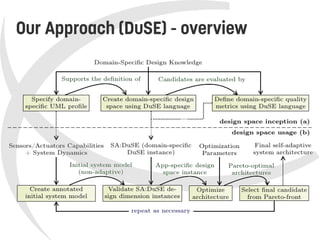
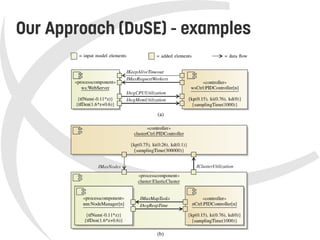
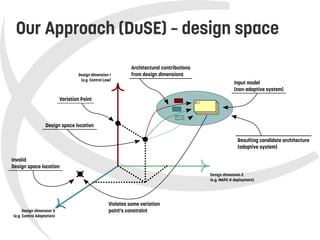
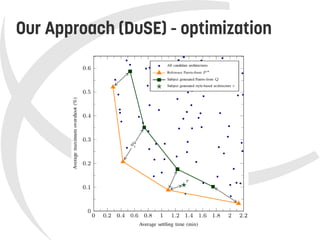
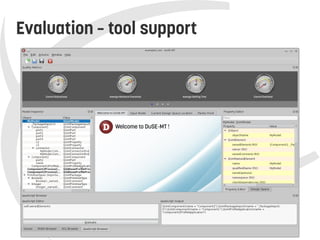
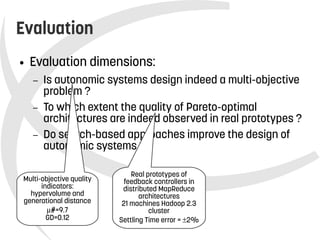
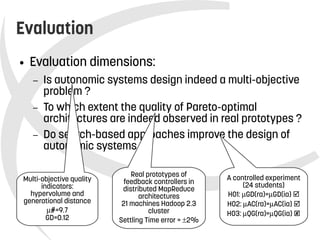
This document presents a model-based approach called DuSE for evaluating trade-offs between feedback control architectures in autonomic systems. DuSE combines metamodeling, design spaces, quality metrics, and multi-objective optimization to enable more disciplined and automated design of autonomic systems. It represents autonomic systems design knowledge systematically and supports informed decision making regarding quality attribute trade-offs. DuSE was evaluated using real prototypes and experiments, finding that autonomic systems design is a multi-objective problem and search-based approaches can improve design.

1.
A Systematic Model-Based Approach
for Feedback Control Trade-Off
Evaluation in Autonomic Systems
Sandro S. Andrade e Raimundo J. de A. Macêdo
Distributed Systems Laboratory (LaSiD)
Department of Computer Science
Federal University of Bahia
{sandros, macedo}@ufba.br
XXXII SBRC – IV Workshop de Sistemas Distribuídos Autonômicos – WoSiDA 2014

2.
Context and Motivation
● Nearly 13 years have elapsed in Autonomic
Systems research field
● Different research communities Different→
underpinnings for self-management:
– Reflexive middleware platforms
– Graph grammars
– Intelligent agents
– Policy-based
– Bio-inspired self-organizing structures

3.
Context and Motivation
● Consequences:
– Lack of organized design knowledge for routine use
– False intuition and design bias
– Sub-optimal architectures for self-management
● A perspective from Software Engineering
● Research questions:
– To which extent may autonomic systems design
knowledge be systematically represented for routine
use ?
– How to support well-informed decision making regarding
quality attribute trade-offs between alternative
architectures ?

4.
Our Approach (DuSE)
● We combine the use of ...
– Metamodeling and Domain-Specific Languages (DSL)
– Structured Architecture Design Spaces
– Architecture Quality Metrics
– Multi-Objective Optimization
● … in order to …
– Enable a more disciplined and automated “handbook”
of autonomic systems design
– Provide a solid basis for choosing between
architectures which exhibit different quality attributes

5.
Our Approach (DuSE) - overview

6.
Our Approach (DuSE) - examples

7.
Our Approach (DuSE) – design space

8.
SA:DuSE – design dimensions
VP11: Proportional
VP12: Proportional-Integral
VP13: Proportional-Integral-Derivative
VP14: Static State Feedback
VP15: Precompensated Static State Feedback
VP16: Dynamic State Feedback
DD1
: Control Law
VP31: Fixed Gain (no adaptation)
VP32: Gain Scheduling
VP33: Model Identification Adaptation Control
DD3
: Control Adaptation
VP21: Chien-Hrones-Reswick, 0 OS, Dist. Rejection
VP22: Chien-Hrones-Reswick, 0 OS, Ref. Tracking
VP23: Chien-Hrones-Reswick, 20 OS, Dist. Rejection
VP24: Chien-Hrones-Reswick, 20 OS, Ref. Tracking
VP25: Ziegler-Nichols
VP26: Cohen-Coon
VP27: Linear Quadratic Regulator
DD2
: Tuning Approach
VP41: Global Control
VP42: Local Control + Shared Reference
VP43: Local Control + Shared Error
DD4
: MAPE Deployment

9.
SA:DuSE – quality metrics
M2
: Average
Settling Time
ME2=
allOwnedElements()→ selectAsType(QParametricController)→sum(stime())
allOwnedElements()→selectAsType(QParametricController)→size()
; whereQParametricController:: stime()=
−4
log(maxi∣pi∣)
;and maxi∣pi∣is themagnitude of thelargest closed−loop pole
M1
: Control
Overhead
ME1=
allOwnedElements()→ selectAsType(QController)→ collect(overhead())→sum ()
allOwnedElements()→selectAsType(QController)→size()
;QController :: overhead()increasingly penalizes VP32, VP33, VP41 and VP43
M4
: Control
Robustness
ME4=
allOwnedElements()→ selectAsType(QController)→collect(robustness())→sum ()
allOwnedElements()→selectAsType(QController)→size()
;QController ::robustness()increasingly penalizesVP31 andVP32
M3
: Average
Maximum Overshoot
ME3=
allOwnedElements()→selectAsType(QParametricController)→sum (maxOS ())
allOwnedElements()→selectAsType(QParametricController)→size()
; whereQParametricController:: maxOS()=
{
0 ;realdominant pole p1
≥0
∣p1∣;real dominant pole p1<0
rπ/∣θ∣
;dominant poles p1, p2=r.e±j. θ}

10.
Our Approach (DuSE) - optimization
● Even small input models generate huge design
spaces:
– 3 controllable components 54,010,152 candidates→
– 4 controllable components 20,415,837,000→
candidates
● Multi-objective Optimization:
– NSGA-II evolutionary backend
– The output is a set of Pareto-optimal architectures:
● They differ only on which quality metric is favored

11.
Our Approach (DuSE) - optimization

12.
Evaluation – tool support

13.
Evaluation
● Evaluation dimensions:
– Is autonomic systems design indeed a multi-objective
problem ?
– To which extent the quality of Pareto-optimal
architectures are indeed observed in real prototypes ?
– Do search-based approaches improve the design of
autonomic systems ?

14.
Evaluation
● Evaluation dimensions:
– Is autonomic systems design indeed a multi-objective
problem ?
– To which extent the quality of Pareto-optimal
architectures are indeed observed in real prototypes ?
– Do search-based approaches improve the design of
autonomic systems ?
Multi-objective quality
indicators:
hypervolume and
generational distance
#=9.7
GD=0.12

15.
Evaluation
● Evaluation dimensions:
– Is autonomic systems design indeed a multi-objective
problem ?
– To which extent the quality of Pareto-optimal
architectures are indeed observed in real prototypes ?
– Do search-based approaches improve the design of
autonomic systems ?
Multi-objective quality
indicators:
hypervolume and
generational distance
#=9.7
GD=0.12
Real prototypes of
feedback controllers in
distributed MapReduce
architectures
21 machines Hadoop 2.3
cluster
Settling Time error = 2%

16.
Evaluation
● Evaluation dimensions:
– Is autonomic systems design indeed a multi-objective
problem ?
– To which extent the quality of Pareto-optimal
architectures are indeed observed in real prototypes ?
– Do search-based approaches improve the design of
autonomic systems ?
Multi-objective quality
indicators:
hypervolume and
generational distance
#=9.7
GD=0.12
Real prototypes of
feedback controllers in
distributed MapReduce
architectures
21 machines Hadoop 2.3
cluster
Settling Time error = 2%
A controlled experiment
(24 students)
H01: GD(ra)=GD(ia) ☑
H02: AC(ra)=AC(ia) ☑
H03: QG(ra)=QG(ia) 

17.
Conclusion
● Limitations:
● Only feedback control concerns up to now
● We assume an initial annotated architecture model is
available
● No guaranteed optimality (local Pareto-fronts)
● Contributions:
● A domain-independent infrastructure for design space
specification
● First search-based approach to self-managed systems
architectural design
● 2nd controlled experiment involving self-managed systems
● A design space exploration tool

18.
Obrigado !
Sandro S. Andrade e Raimundo J. de A. Macêdo
Distributed Systems Laboratory (LaSiD)
Department of Computer Science
Federal University of Bahia
{sandros, macedo}@ufba.br