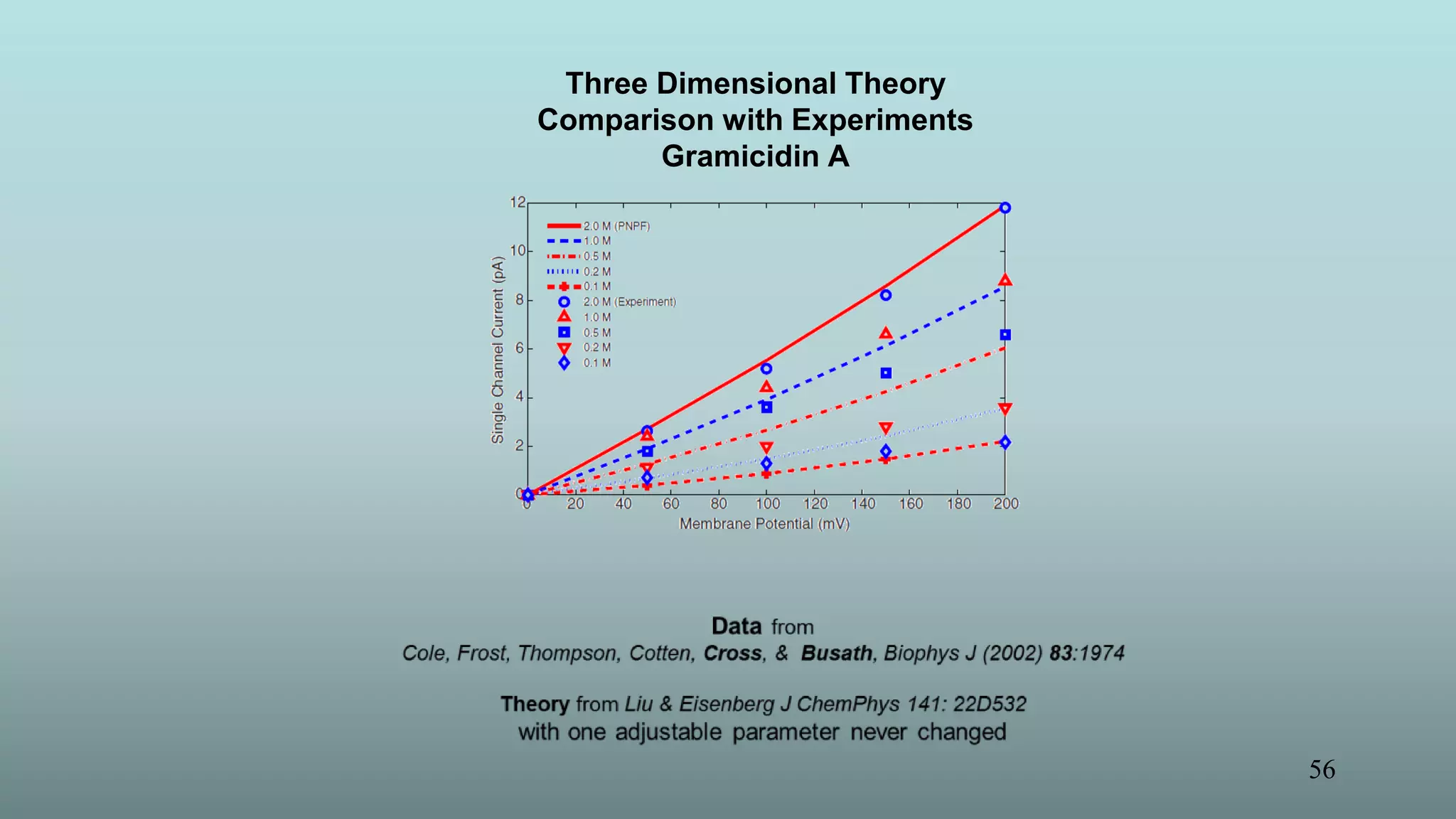
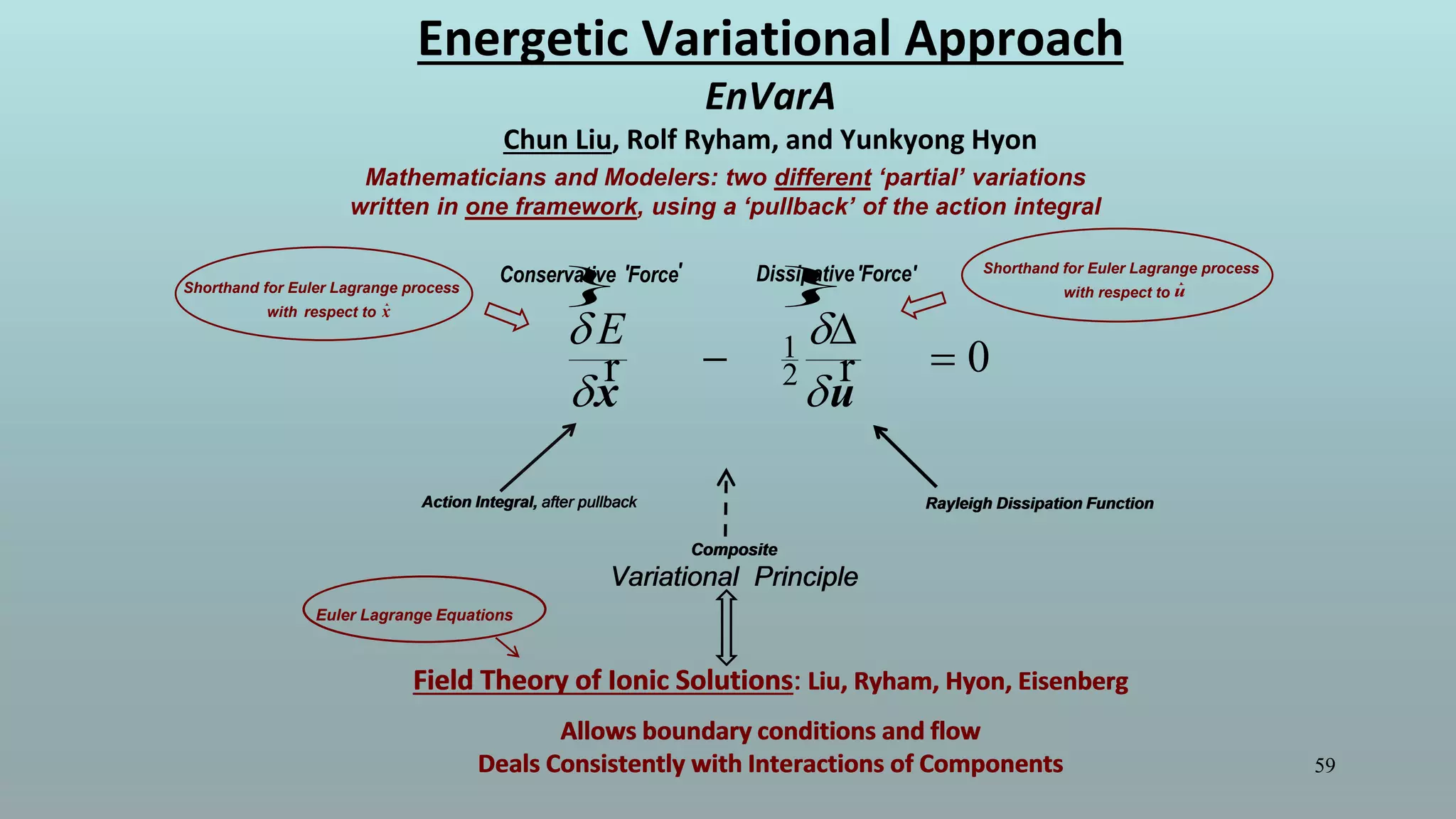
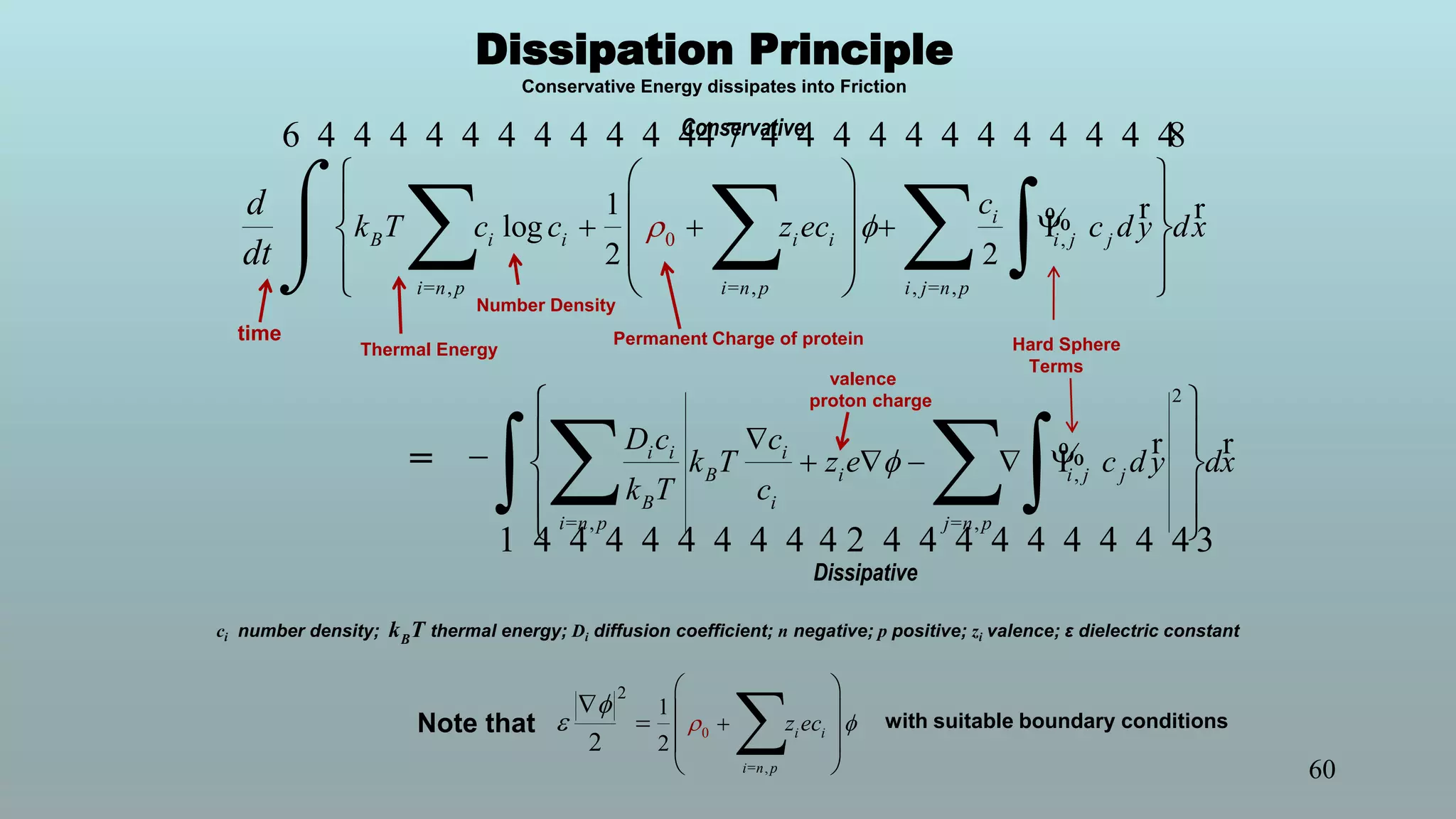
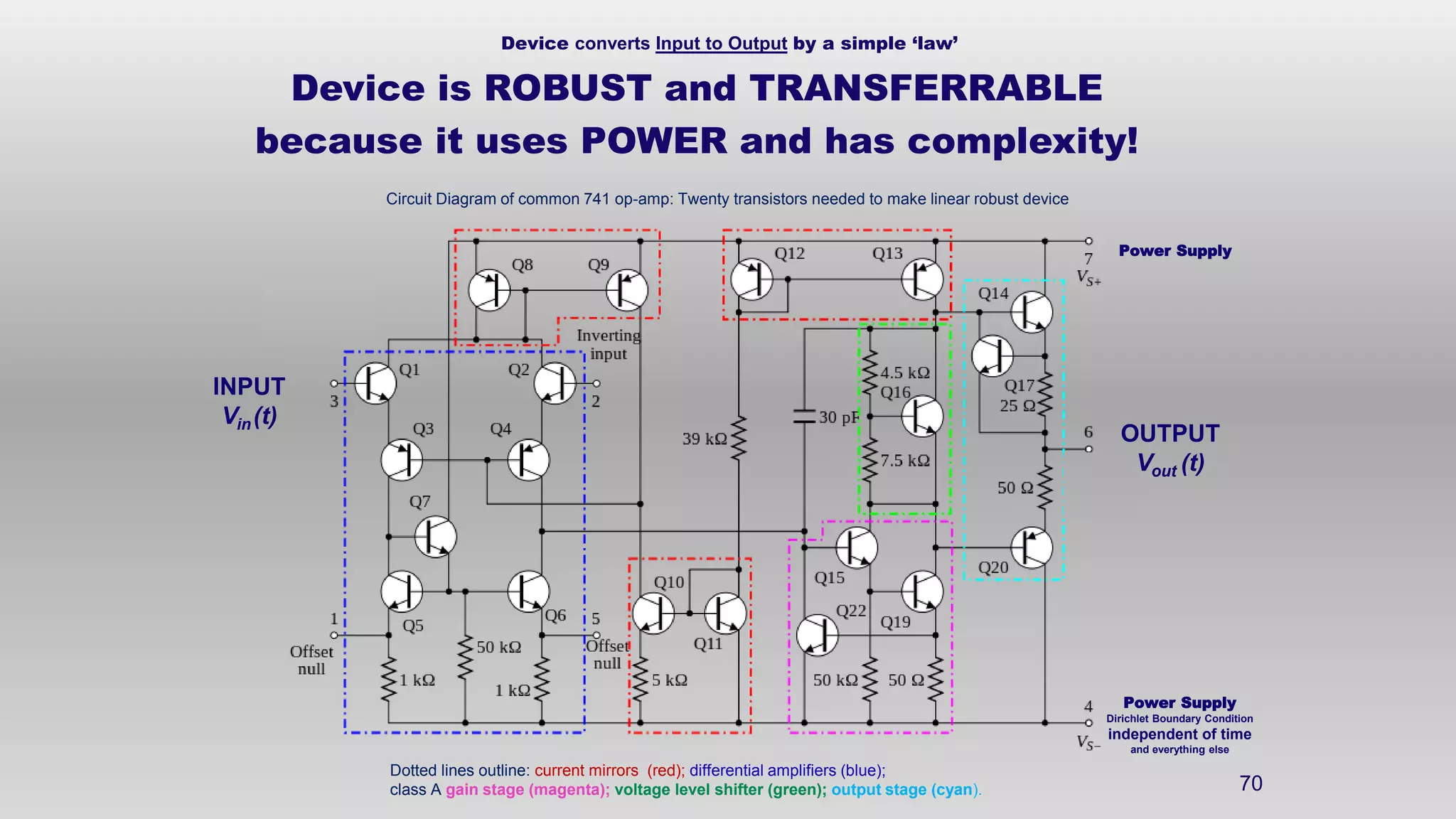
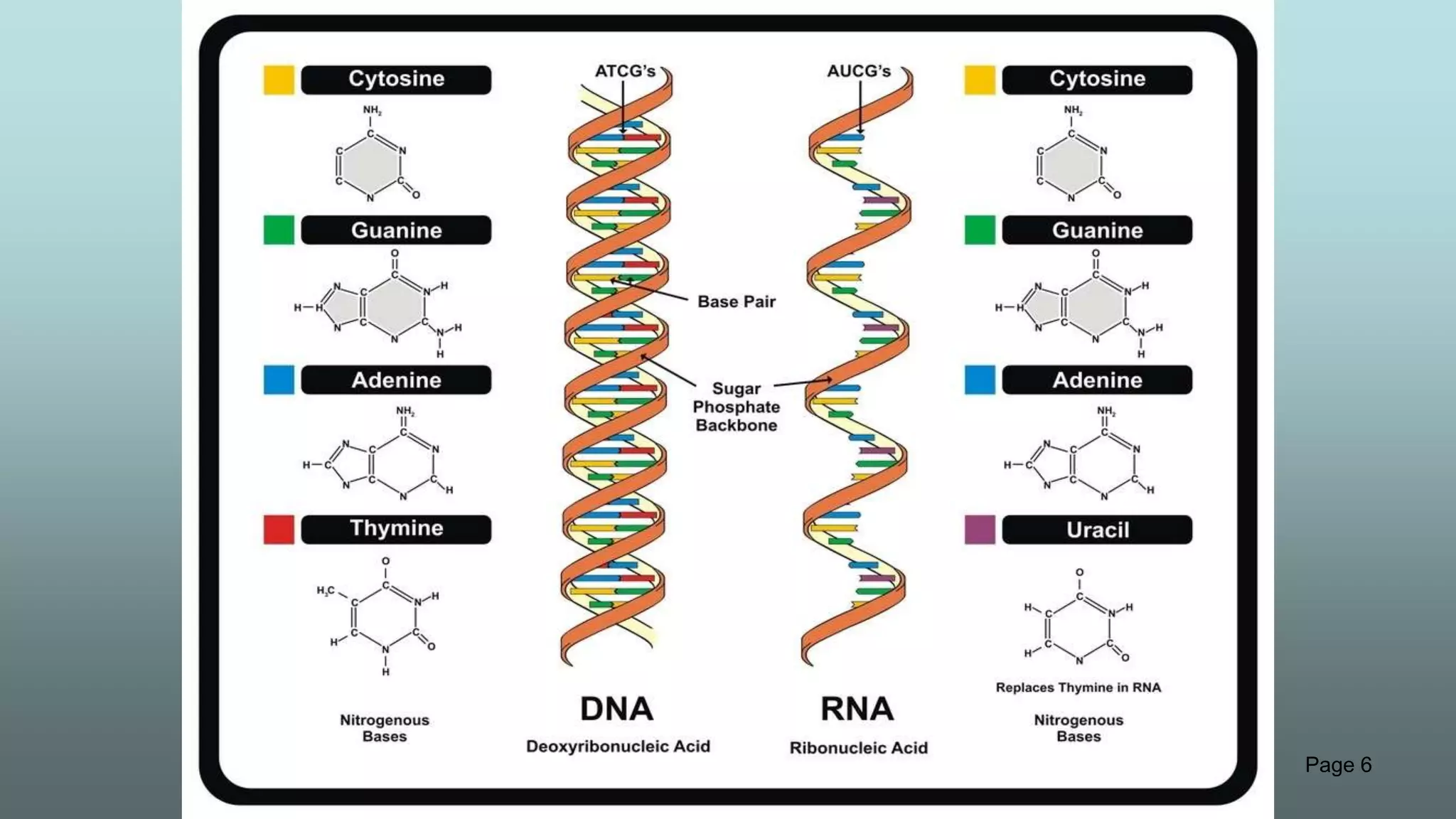
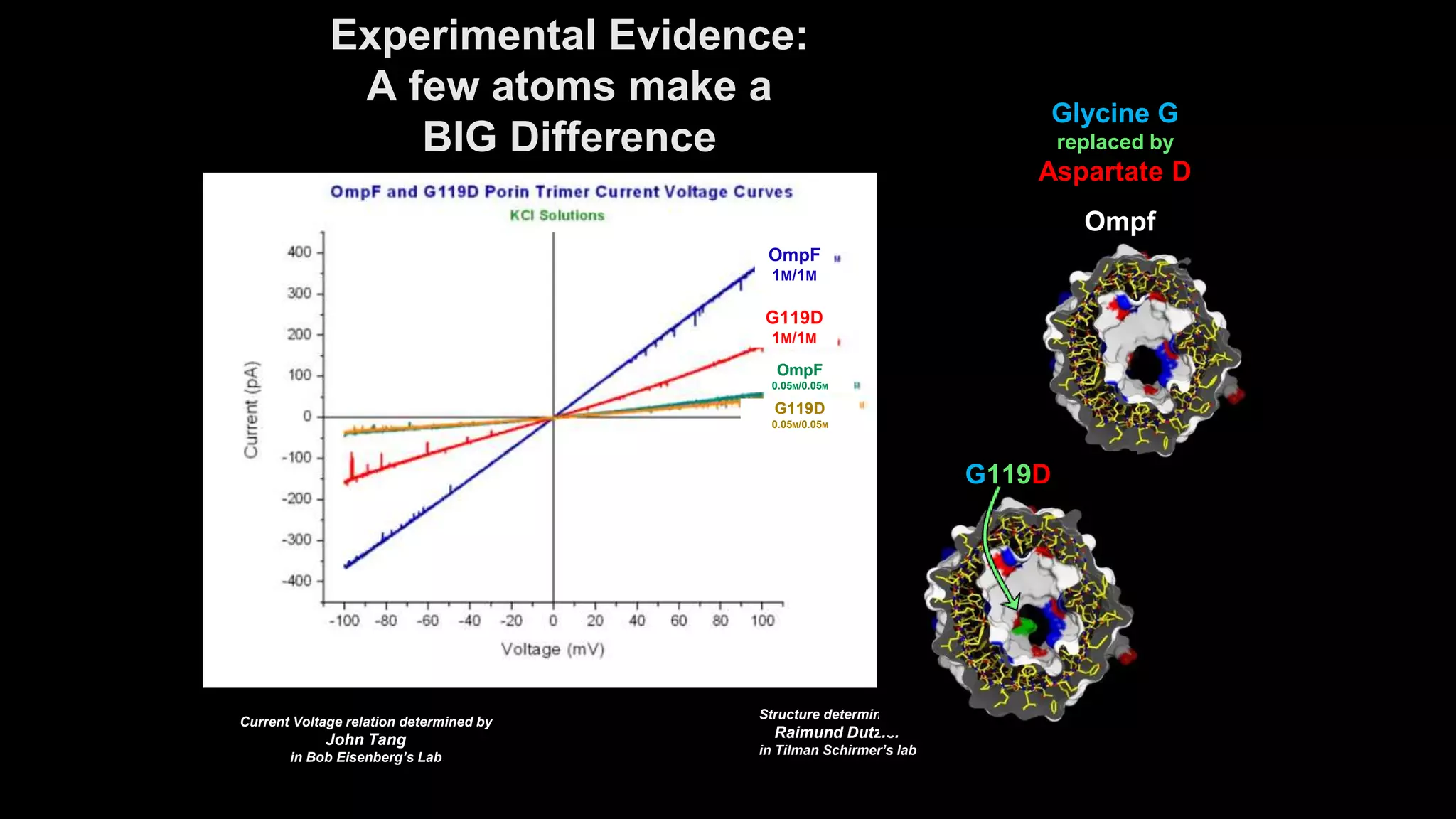
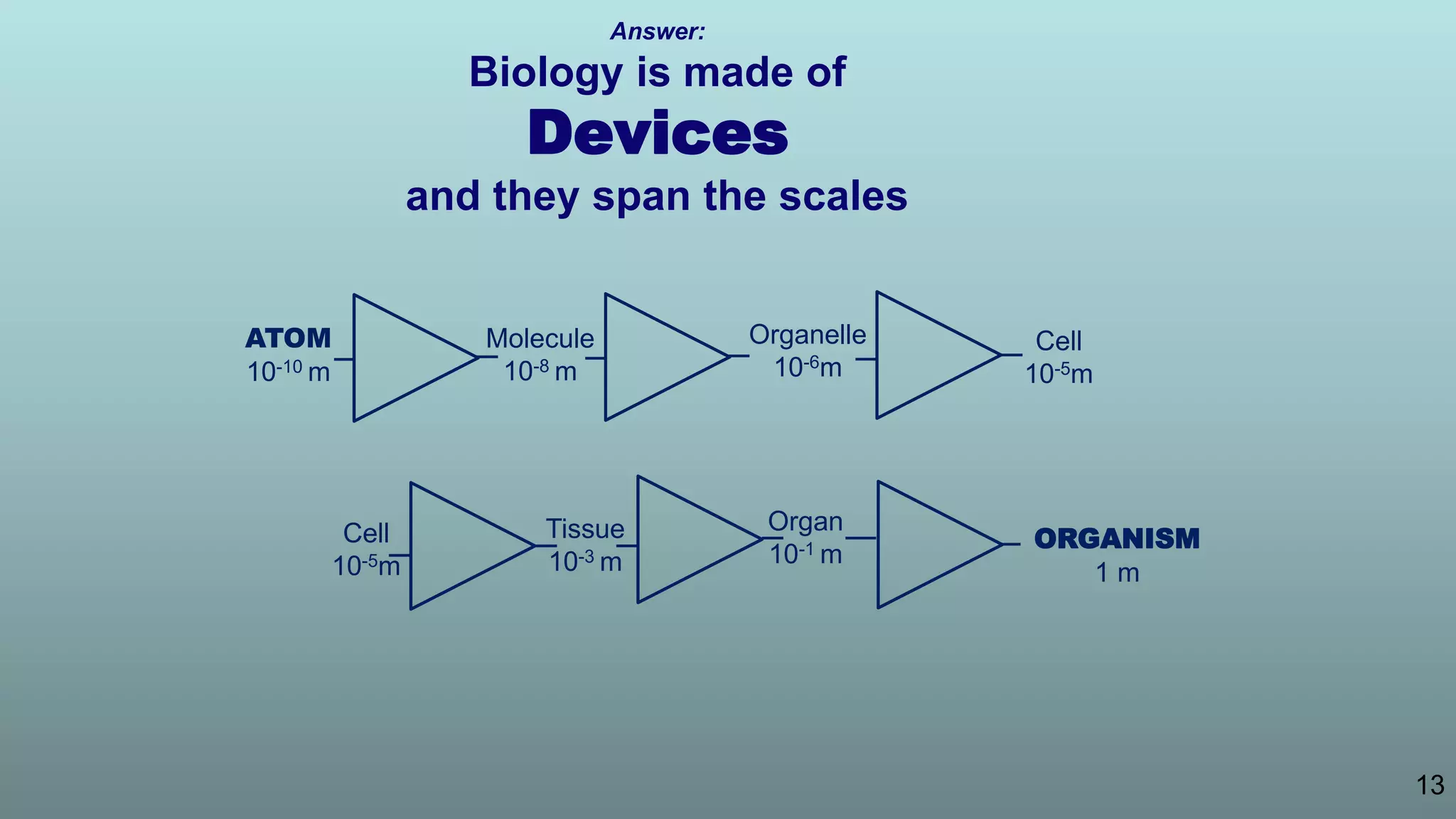
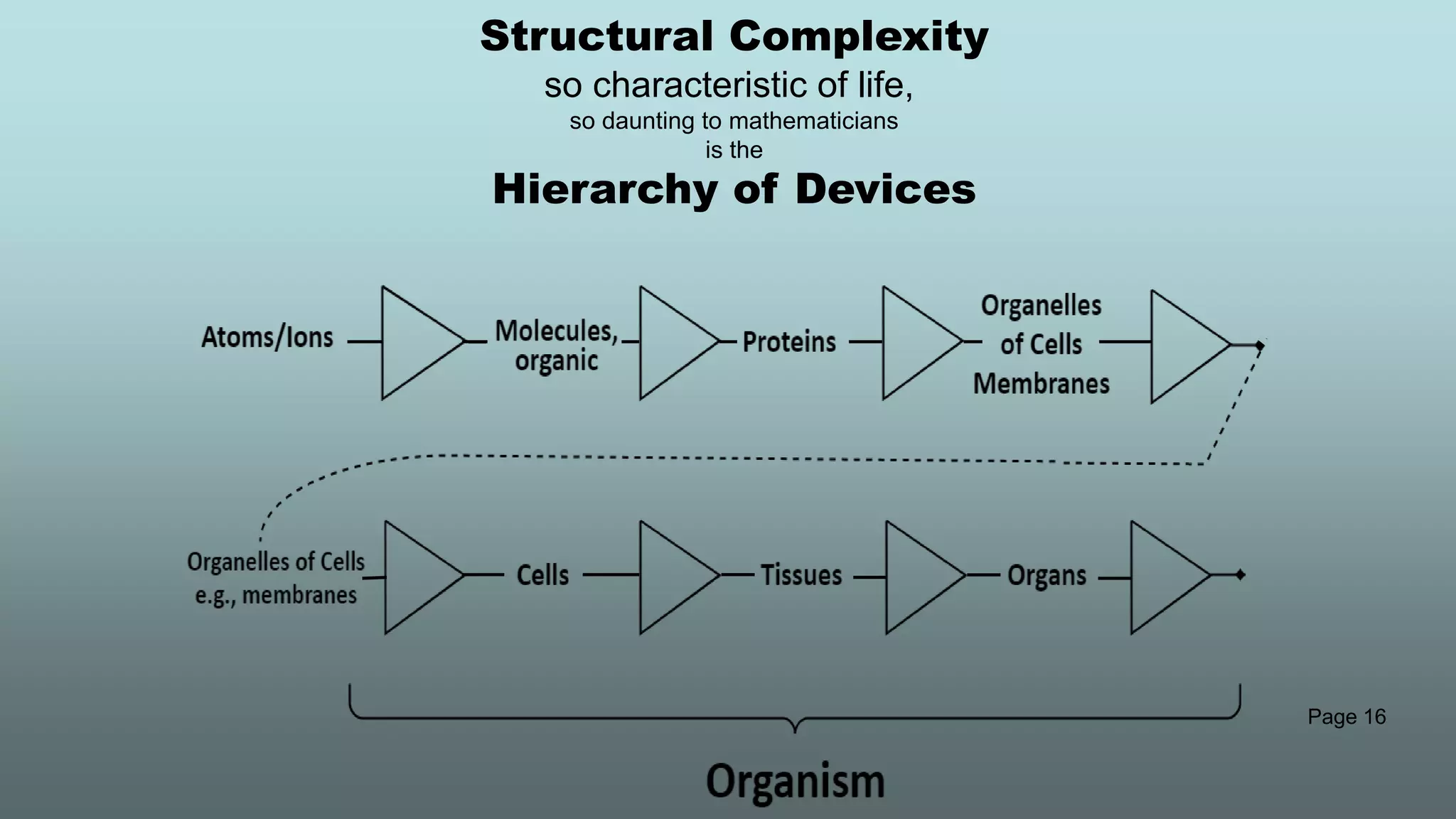
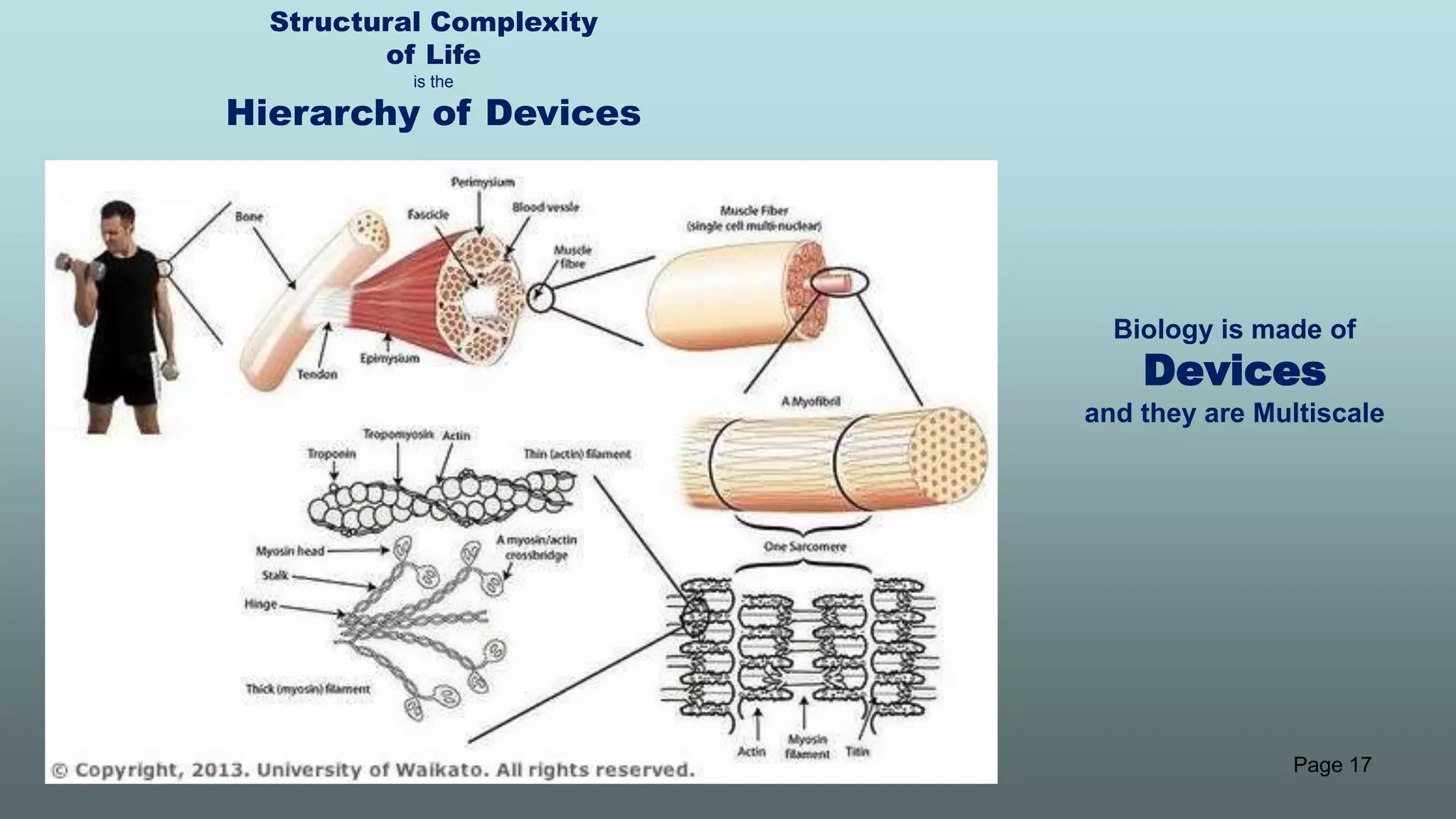
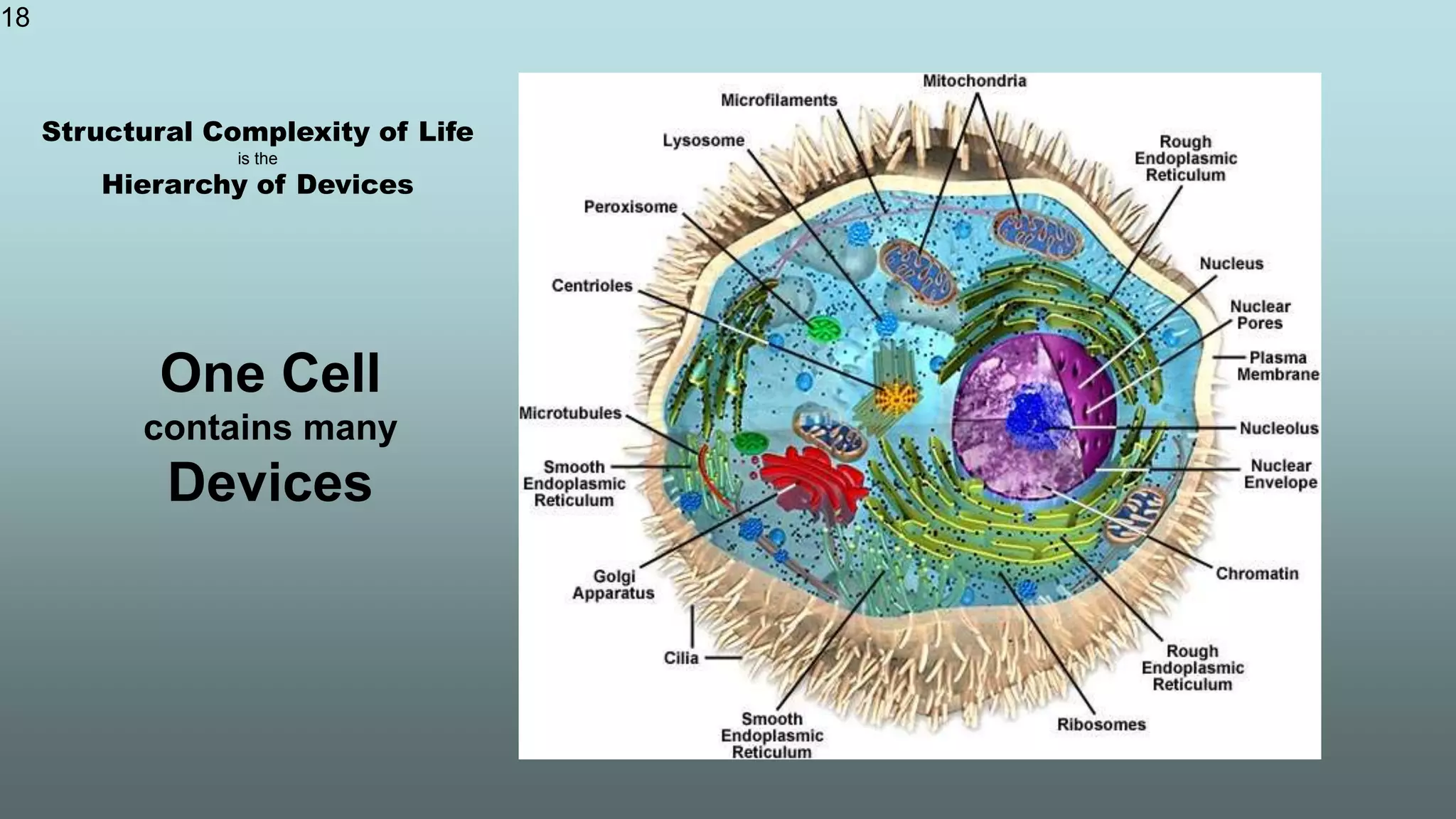
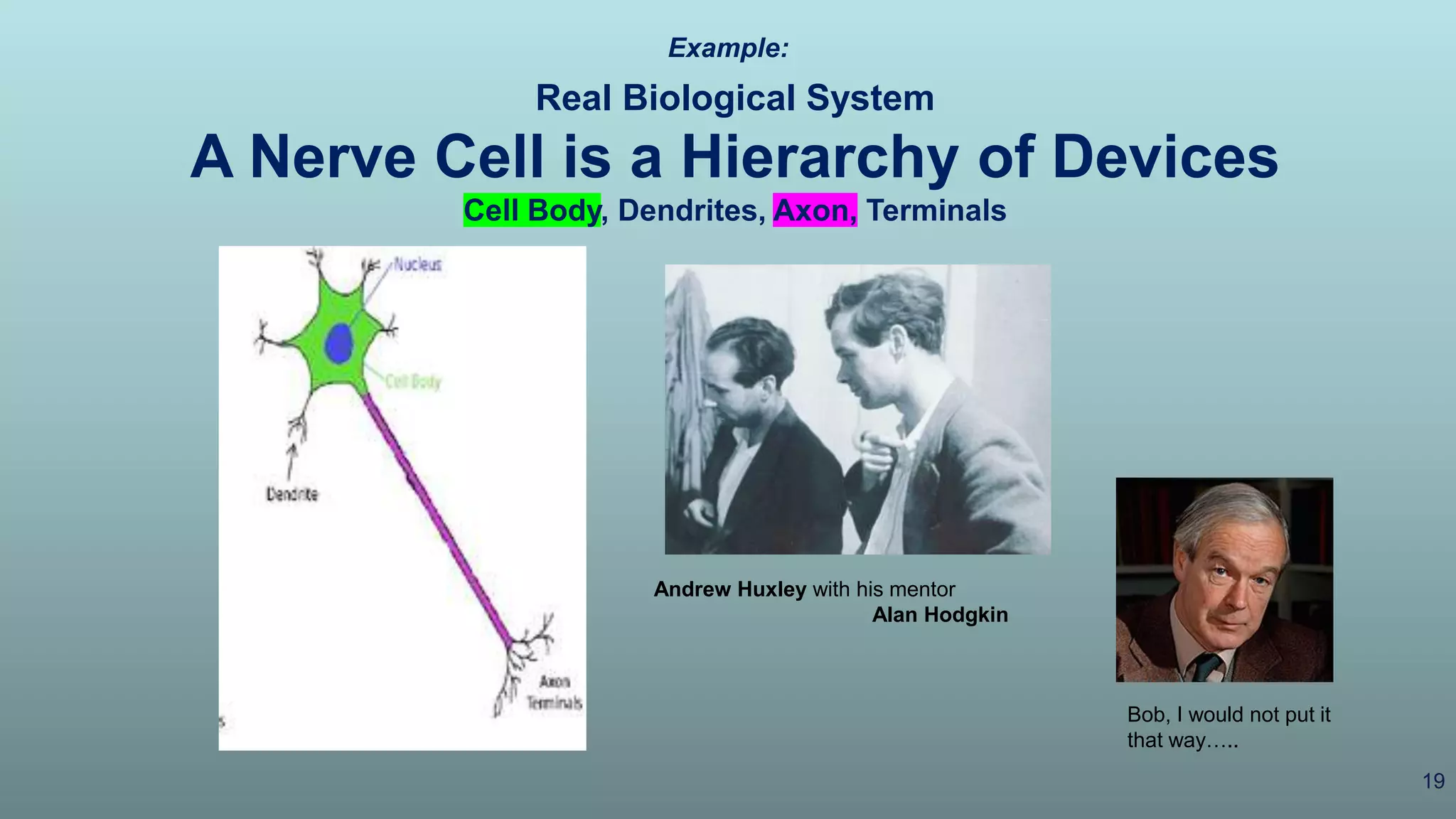
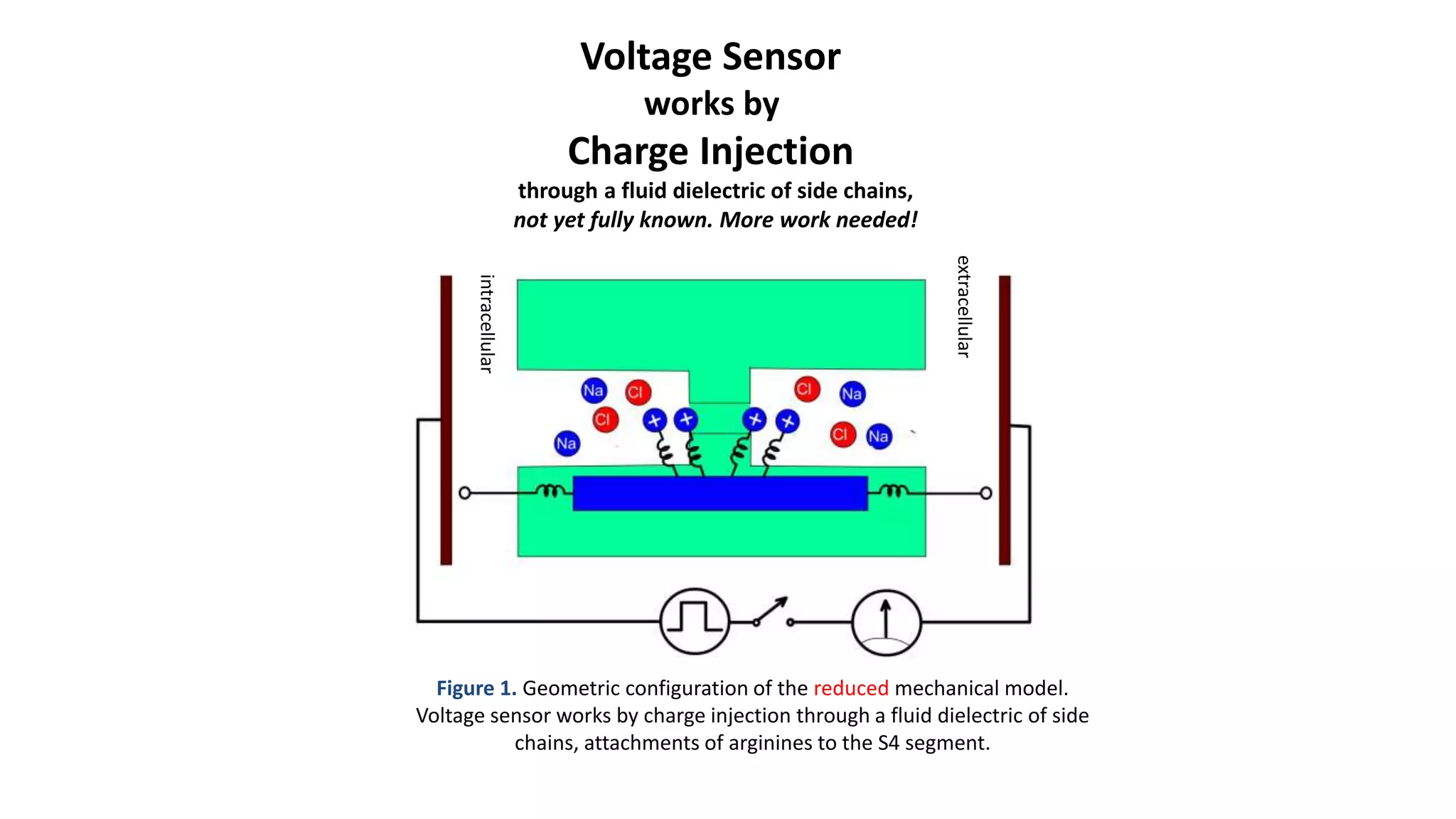
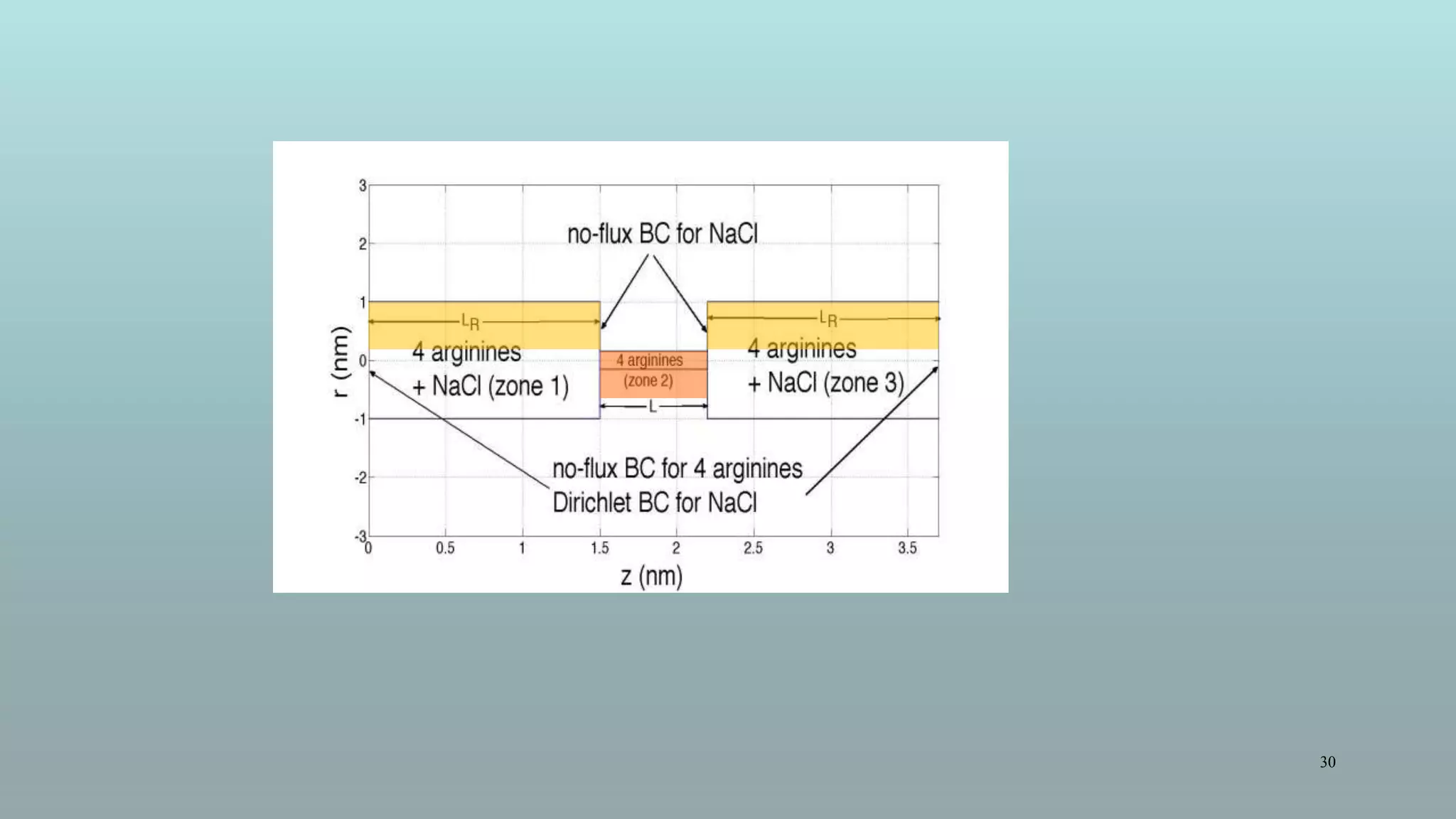
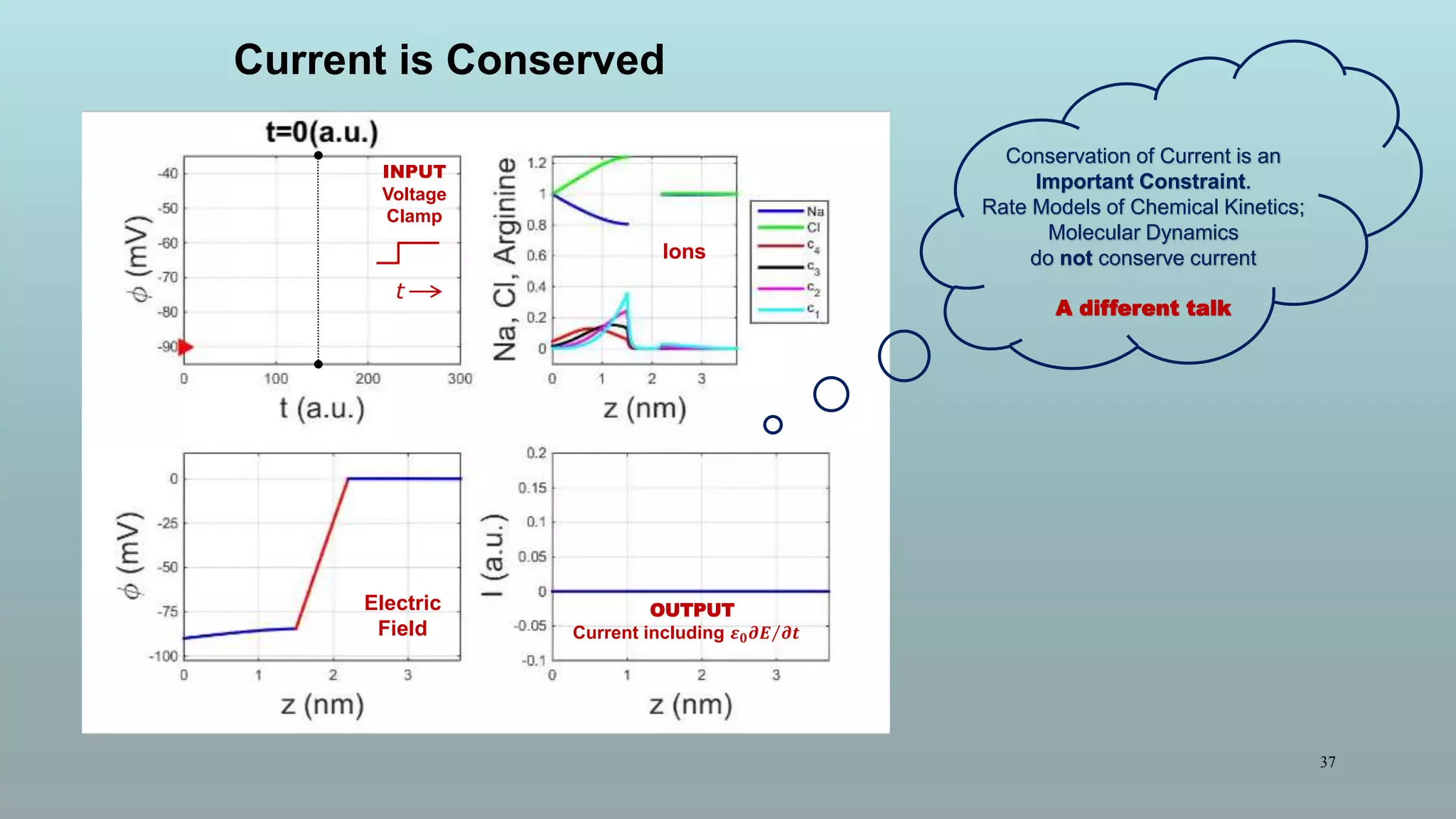
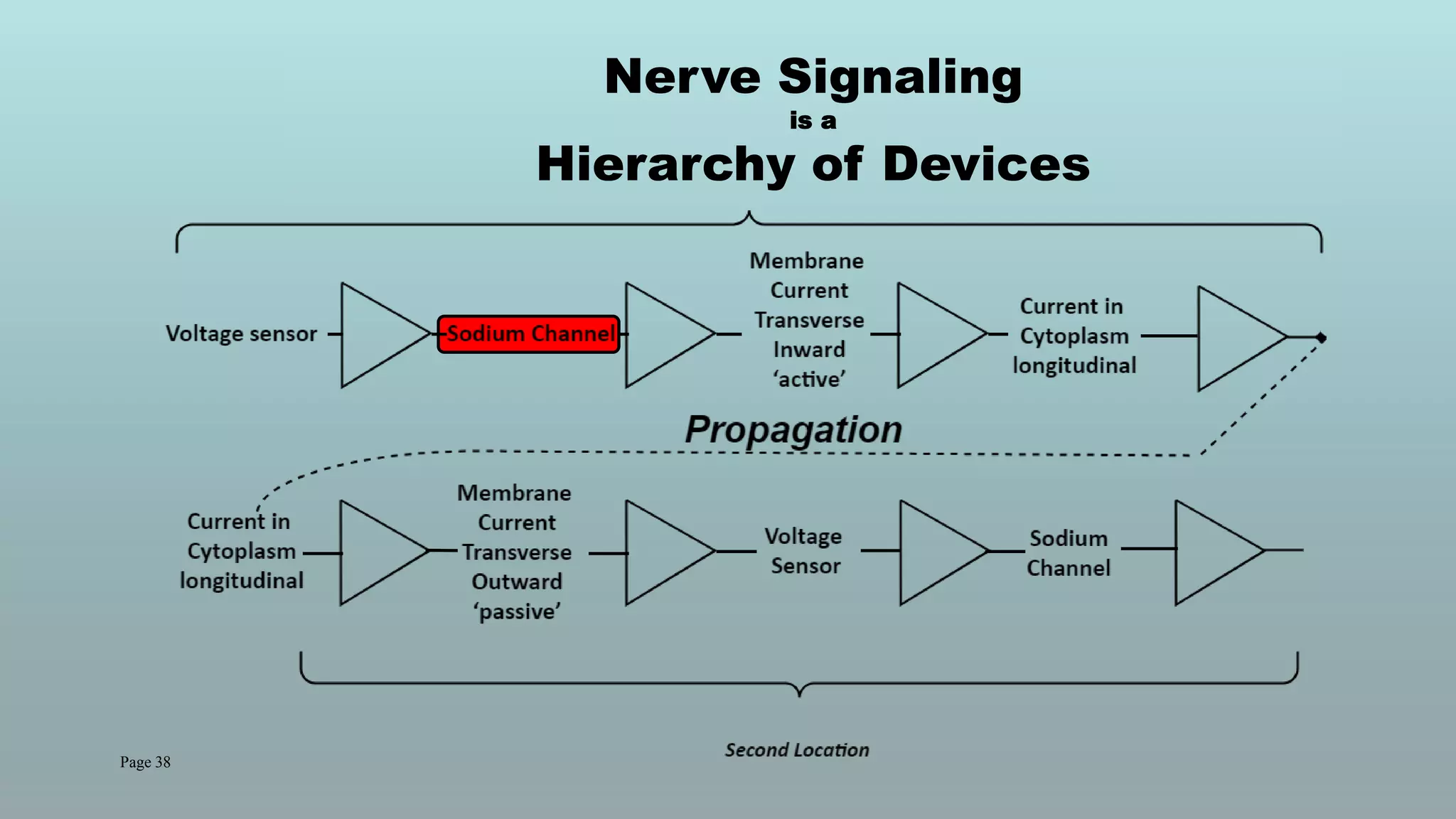
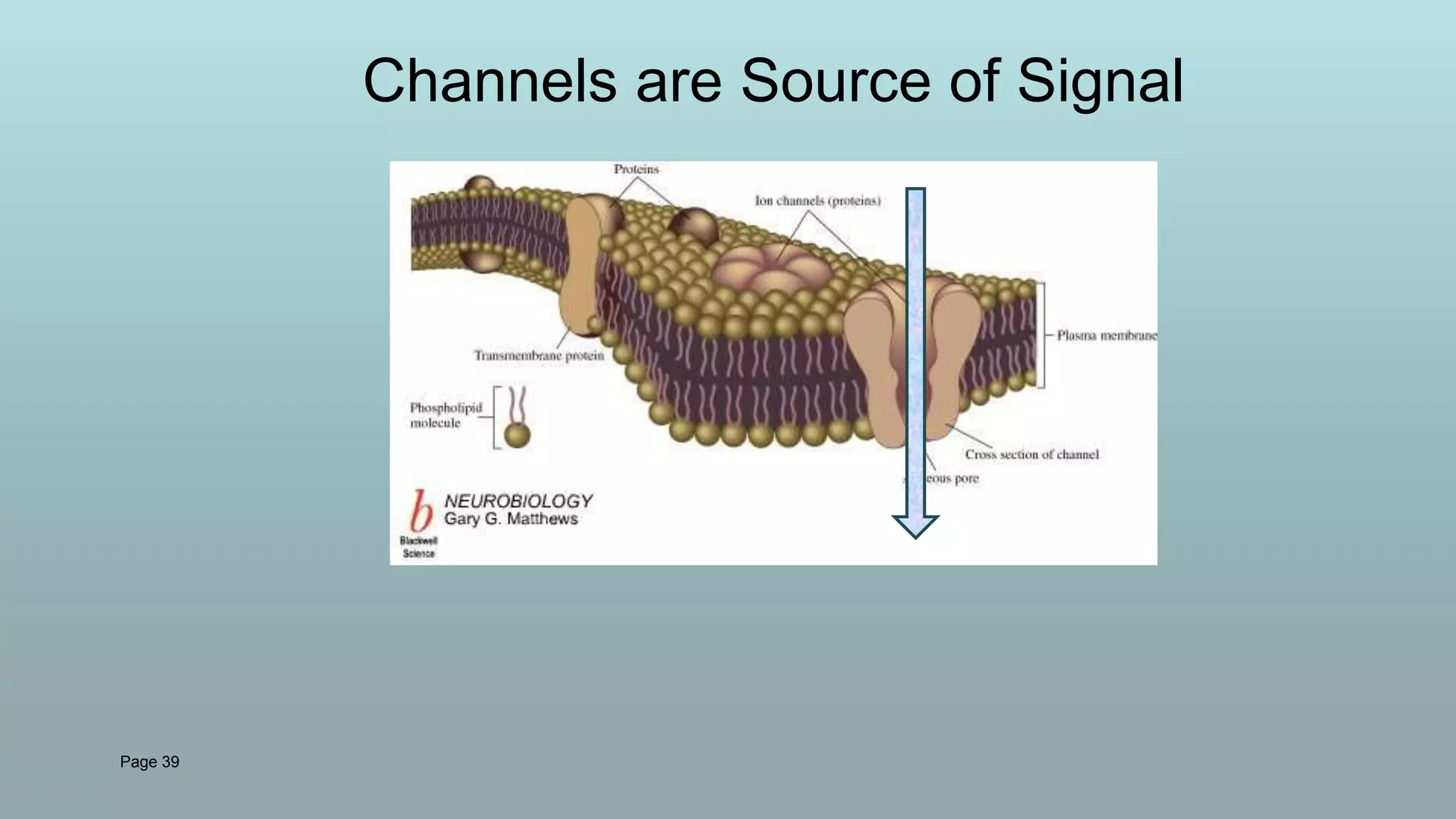
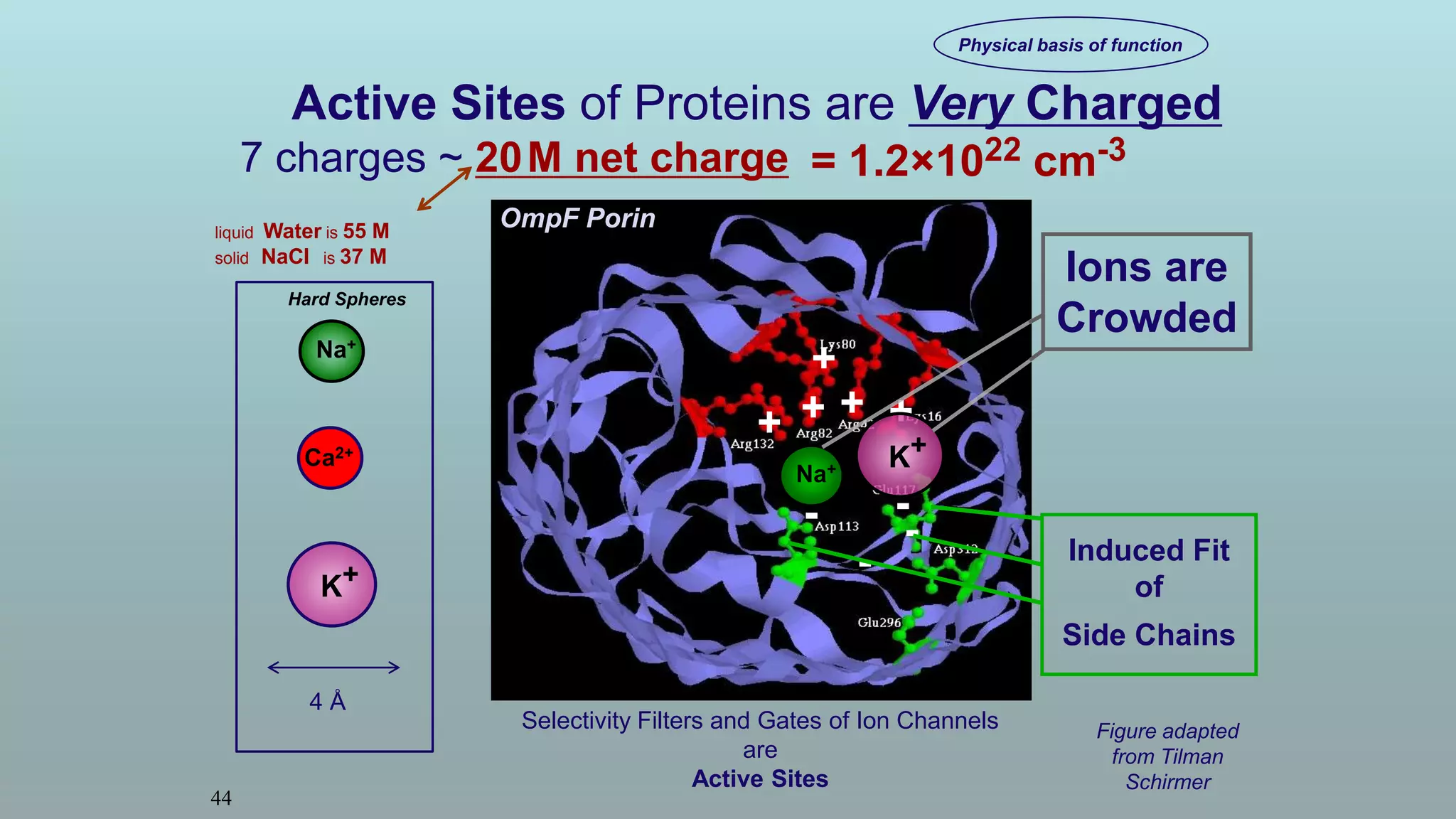
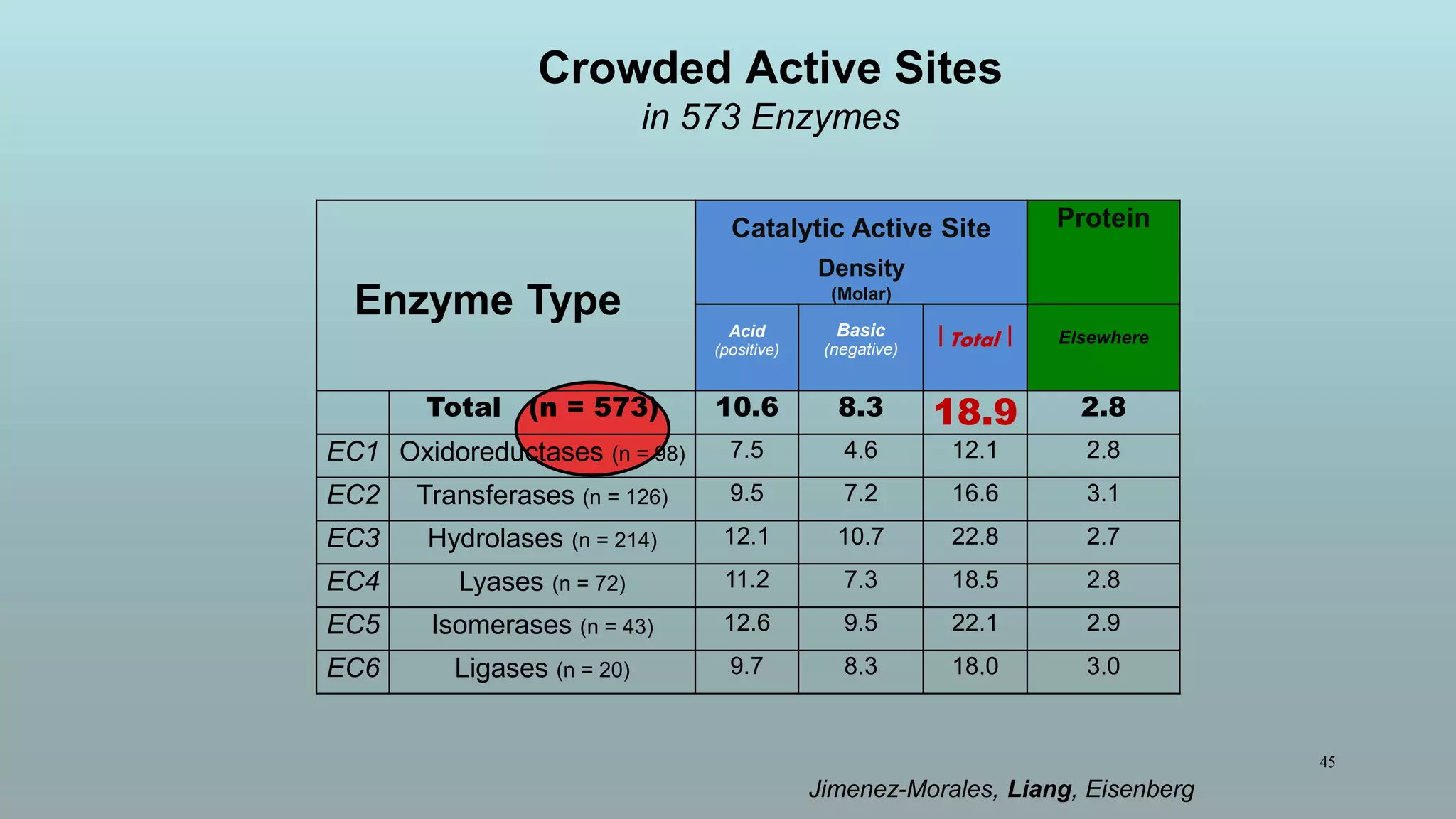
The document discusses the hierarchy of devices in biological structures and their ability to control and influence vast numbers of atoms, suggesting that life is characterized by complex multiscale interactions. It addresses traditional statistical mechanics' limitations in explaining how a few thousand atoms can influence systems containing 10^25 atoms, emphasizing the structural complexity and electric interactions in biological systems. The insights stem from various studies and experiments, revealing the significant role of ion channels and the implications of crowding on biological functionality.
















![Page 35
Figure 9. (a) Time courses of subtracted gating current [A1] with voltage rising
from -90mV to V mV at t=10, holds on till t=150, and drops back to -90mV,
where V=-62, -50, … -8 mV. (b) τ2 versus V compared with experiment [7].
Fitting Data](https://image.slidesharecdn.com/lifeisdifferent-180307085518/75/What-is-different-about-life-it-is-inherited-oberwolfach-march-7-1-2018-35-2048.jpg)
![Page 36
Figure 3. (a) QV curve and comparison with [7]. Steady-state distributions for Na, Cl
and arginines at (b) V=-90mV, (c) V=-48mV, (d) V=-8mV.
Fitting Data](https://image.slidesharecdn.com/lifeisdifferent-180307085518/75/What-is-different-about-life-it-is-inherited-oberwolfach-march-7-1-2018-36-2048.jpg)







![54
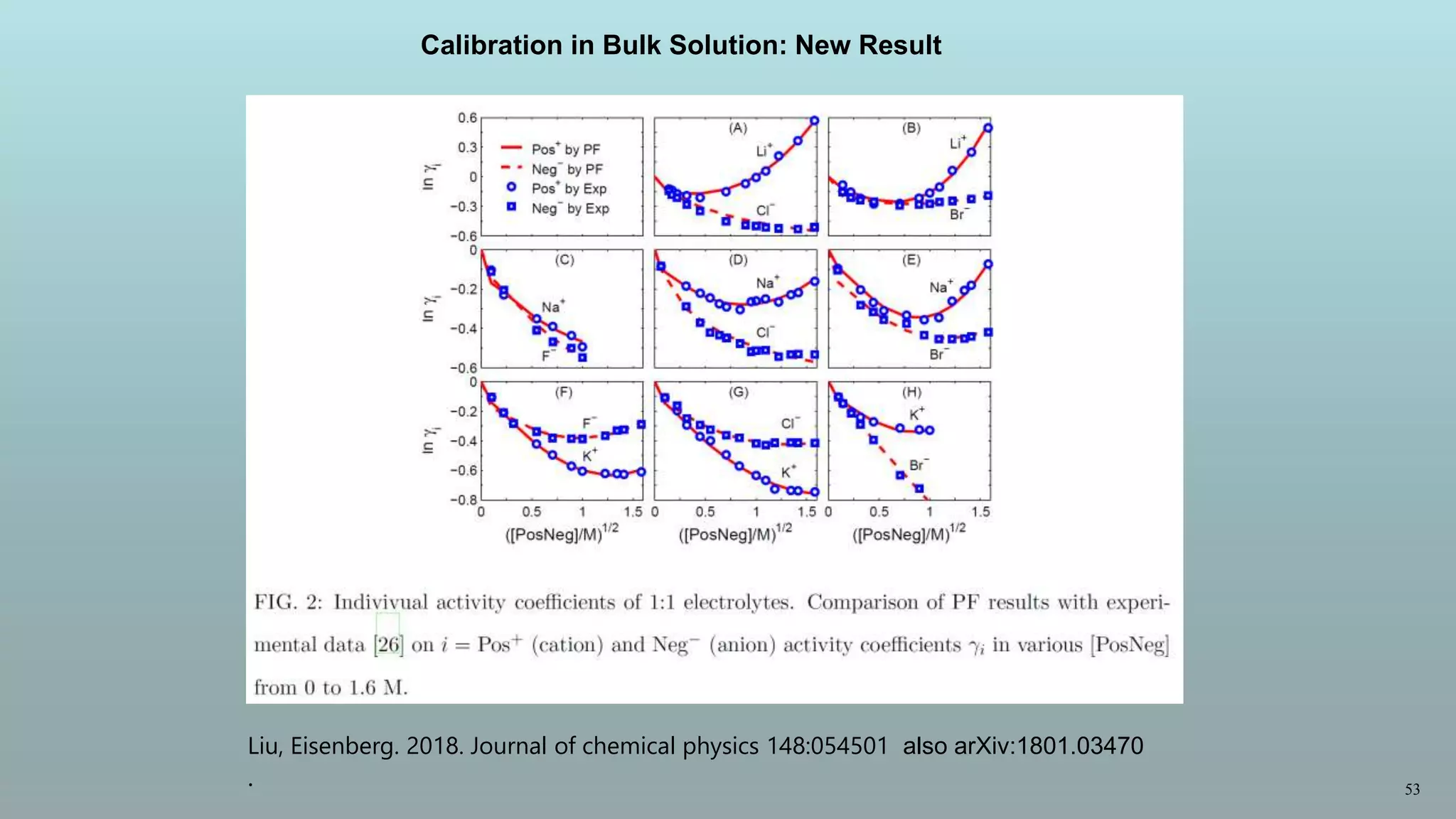
Individual activity coefficients of 2:1 electrolytes.
Comparison of PF results with experimental
data [26] on i = Pos2+ (cation) and Neg− (anion) activity coefficients γi in various [PosNeg2]
from 0 to 1.5 M.
Calibration in Bulk Solution:
New Result](https://image.slidesharecdn.com/lifeisdifferent-180307085518/75/What-is-different-about-life-it-is-inherited-oberwolfach-march-7-1-2018-54-2048.jpg)
![Na Channel
55
Signature of Cardiac Calcium Channel CaV1.n
Anomalous* Mole Fraction (non-equilibrium)
Liu & Eisenberg (2015) Physical Review E 92: 012711
*Anomalous because CALCIUM CHANNEL IS A SODIUM CHANNEL at [CaCl2] 10-3.4
Ca2+ is conducted for [Ca2+] > 10-3.4, but Na+ is conducted for [Ca2+] <10-3.
Ca Channel](https://image.slidesharecdn.com/lifeisdifferent-180307085518/75/What-is-different-about-life-it-is-inherited-oberwolfach-march-7-1-2018-55-2048.jpg)