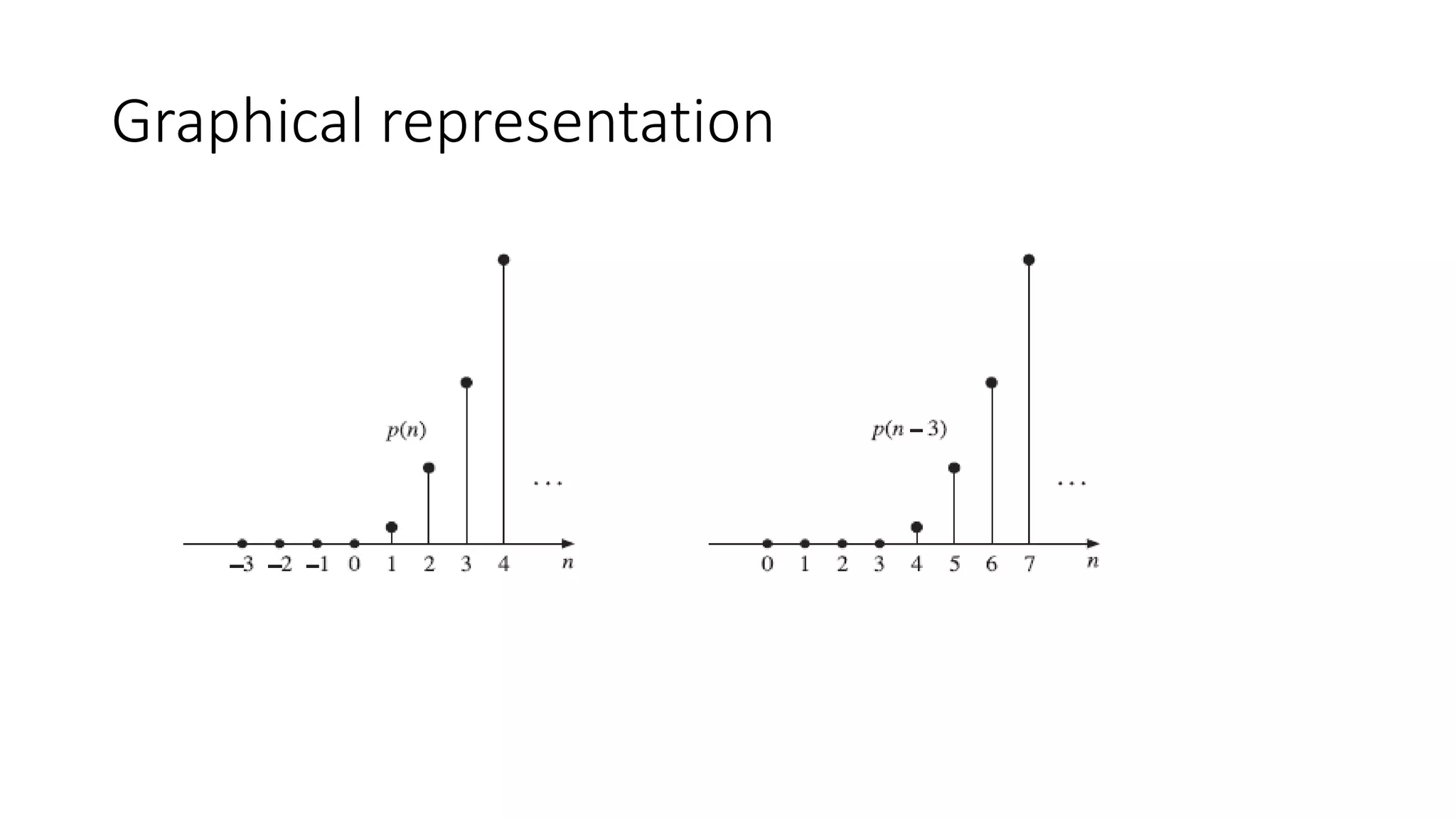
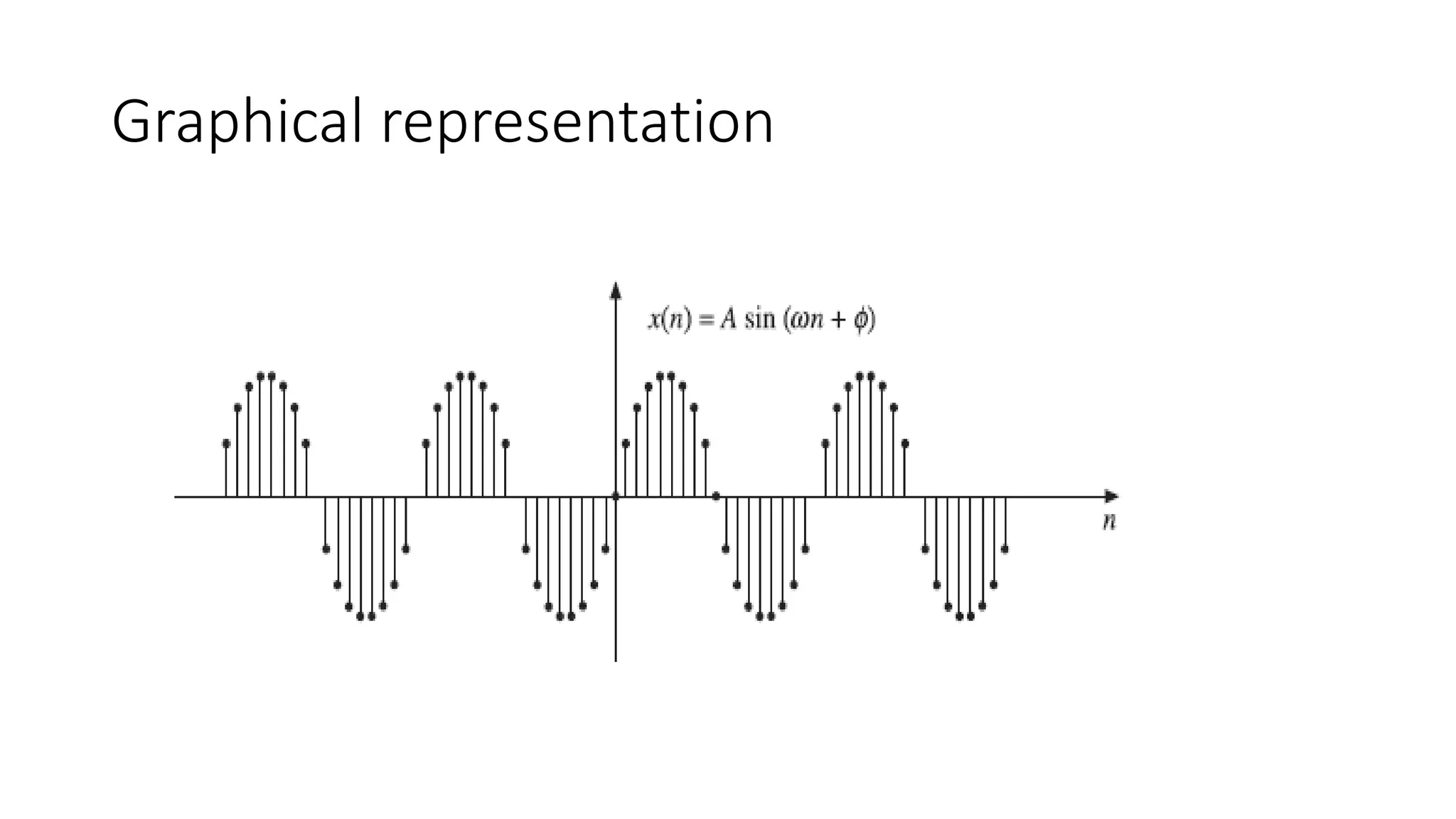
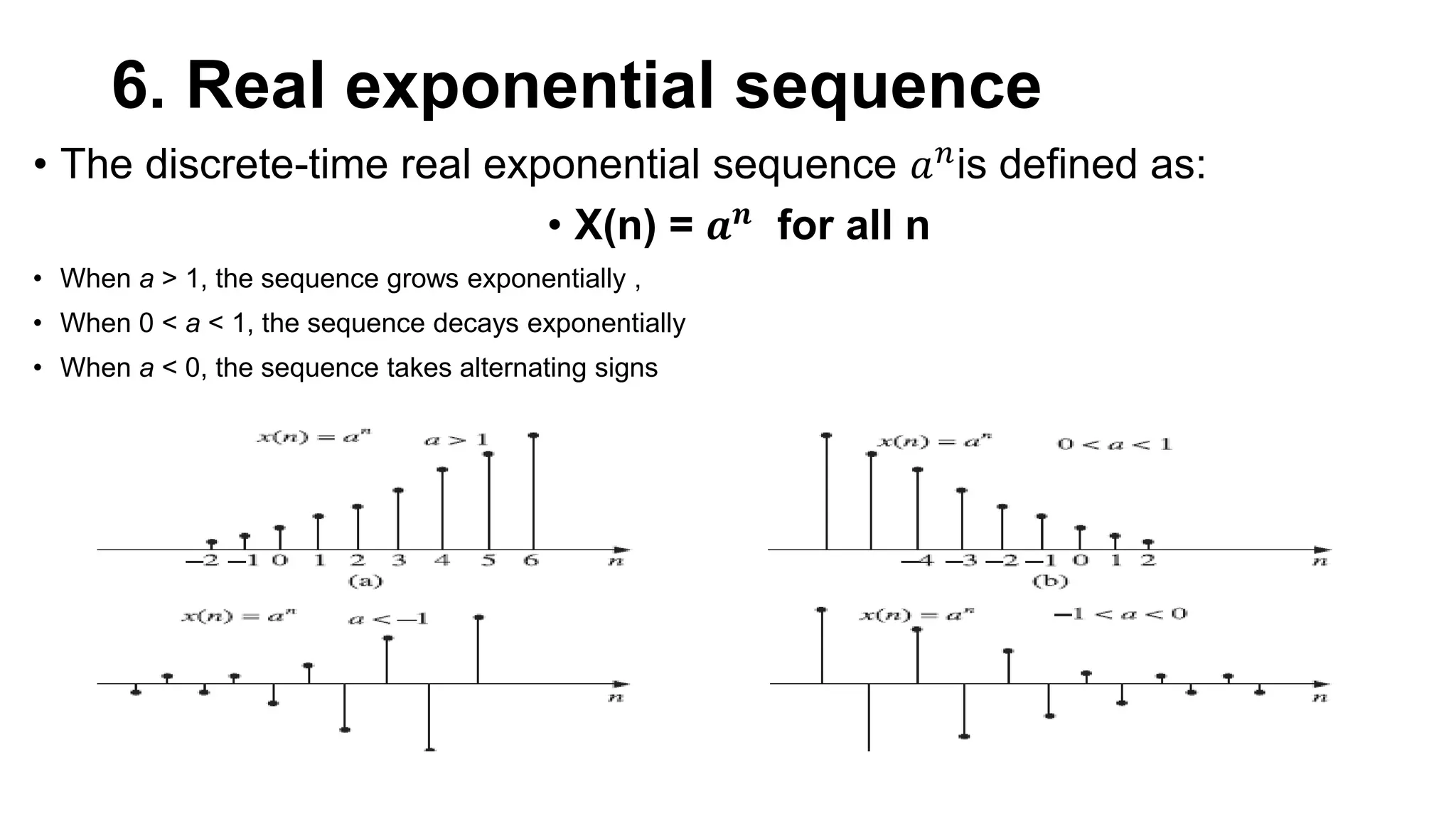
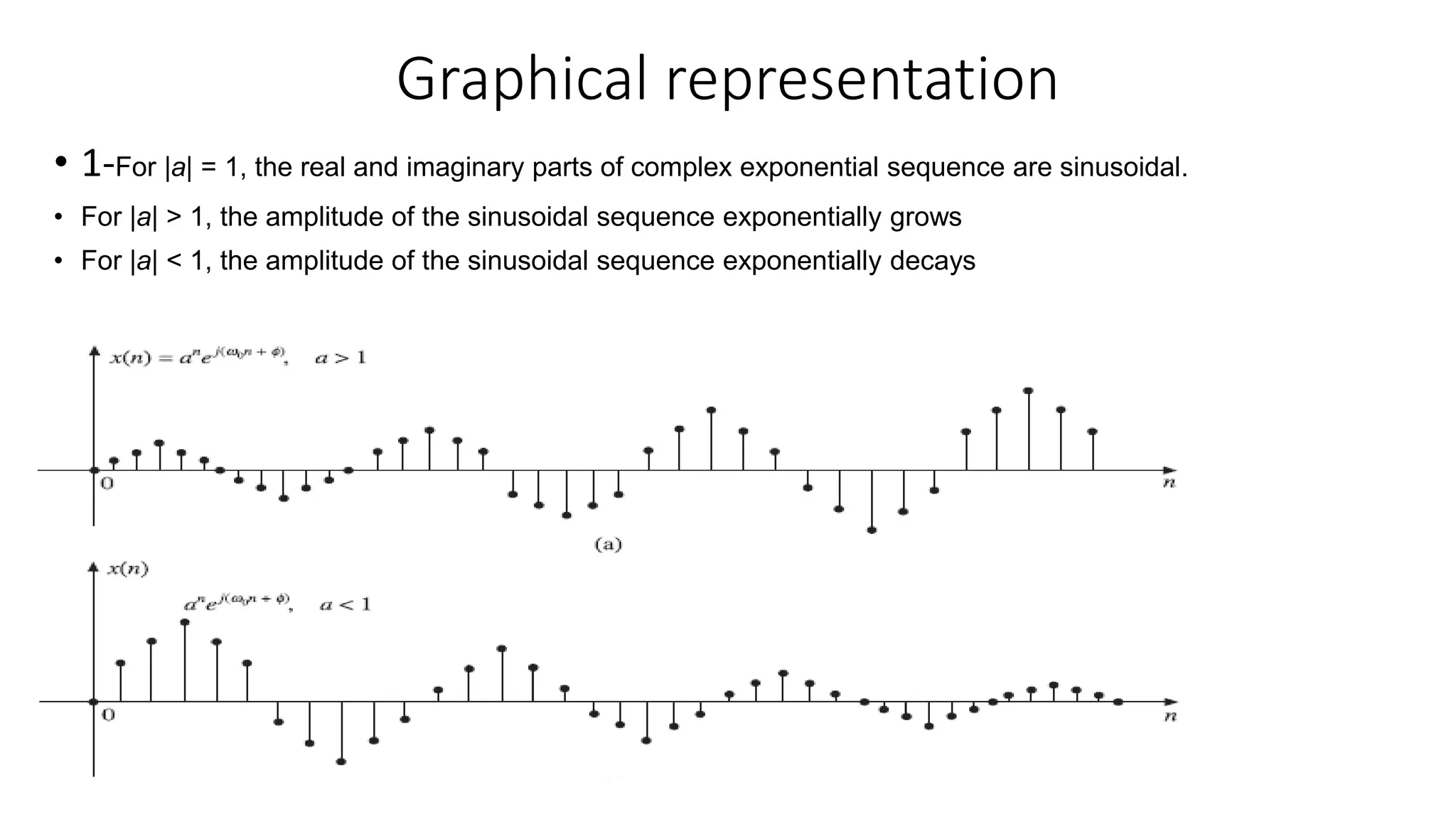
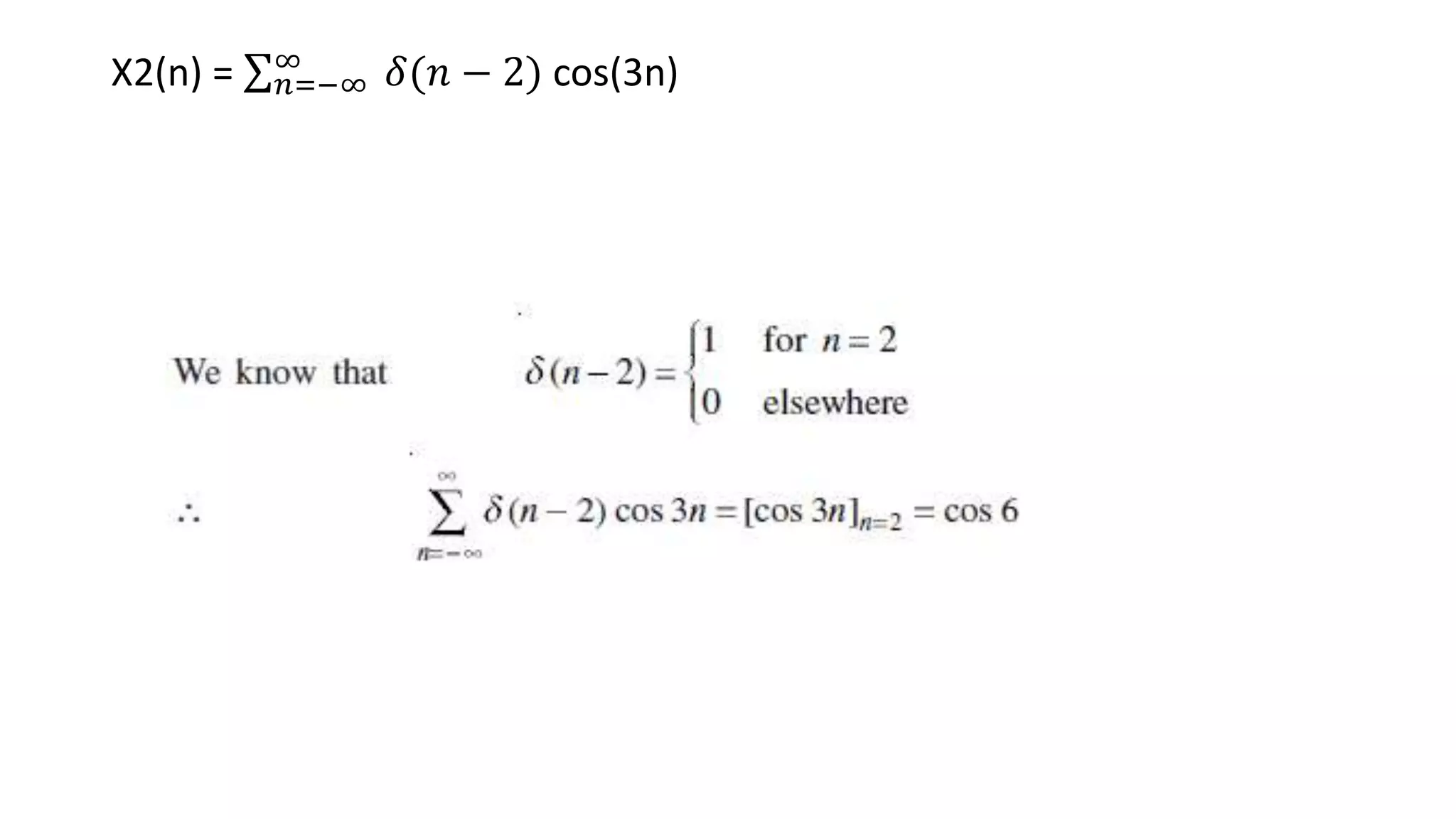This document defines and provides graphical representations of several basic discrete-time sequences important in digital signal processing, including the unit parabolic sequence, unit impulse sequence, sinusoidal sequence, real exponential sequence, and complex exponential sequence. It also discusses properties such as periodicity and growth/decay for these sequences. Examples are provided of summations involving the unit impulse sequence combined with other sequences.

1. Digital Signal
Processing
DSP
Dr. Noura ali
EEC 225
MTE 241
Week 3 lec 3

2. 3. Unit parabolic sequence
• The discrete-time unit parabolic sequence p(n) is defined as:
• P(n) =
𝑛2
2
u(n)
• The shifted version of the discrete-time unit parabolic sequence p(n – k) is
defined as:

3. Graphical representation

4. 4. Unit impulse sequence (unit sample
sequence)
• The discrete-time unit impulse function 𝛿(n), also called unit sample
sequence, is defined as:
• It is zero everywhere, except at n = 0, where its value is unity. It is the most widely used elementary
signal used for the analysis of signals and systems.
• The shifted unit impulse function 𝛿(n – k) is defined as:

5. Graphical representation
• Properties

6. Relation between unit impulse sequence and
unit step sequence
• 1- 𝑈 𝑛 = 𝑚=0
𝑛
𝛿(𝑚)
• 2- 𝛿 𝑛 = U(n) – U(n-1)

7. 5. Sinusoidal sequence
• The discrete-time sinusoidal sequence is given by:
• X(n) = A sin (𝝎n+∅)
• where A is the amplitude, 𝝎 is angular frequency, ∅ is phase angle in radians and n
is an integer.
• The period of the discrete-time sinusoidal sequence is: (N =
𝟐𝝅
𝝎
*m) , where m is
integer
•  All continuous-time sinusoidal signals (sin wt) are periodic, but discrete-time
sinusoidal (sin wn) sequences may or may not be periodic depending on the value of
ω
•  For a discrete-time signal to be periodic, the angular frequency ω must be a
rational multiple of 2.

8. Graphical representation

9. comparison

10. 6. Real exponential sequence
• The discrete-time real exponential sequence 𝑎𝑛is defined as:
• X(n) = 𝒂𝒏 for all n
• When a > 1, the sequence grows exponentially ,
• When 0 < a < 1, the sequence decays exponentially
• When a < 0, the sequence takes alternating signs

11. 7. Complex exponential sequence
• The discrete-time complex exponential sequence is
defined as:
• X(n) = 𝒂𝒏 𝒆(𝒋 𝝎𝟎 𝒏+ ∅)
•= 𝒂𝒏
cos (𝝎𝟎 𝒏 + ∅) +j 𝒂𝒏
sin(𝝎𝟎 𝒏 + ∅)

12. Graphical representation
• 1-For |a| = 1, the real and imaginary parts of complex exponential sequence are sinusoidal.
• For |a| > 1, the amplitude of the sinusoidal sequence exponentially grows
• For |a| < 1, the amplitude of the sinusoidal sequence exponentially decays

13. Examples: find the summation?
• X1(n) = 𝑛=−∞
∞
𝑒3𝑛
𝛿(𝑛 − 3)

14. X2(n) = 𝑛=−∞
∞ 𝛿(𝑛 − 2) cos(3n)

15. X3(n) = 𝑛=−∞
∞
𝑛2
𝛿(𝑛 + 4)

16. X4(n) = 𝑛=−∞
∞
𝑒𝑛2
𝛿(𝑛 − 2)

17. X5(n) = 𝑛=0
∞
4𝑛
𝛿(𝑛 + 1)

18. • Thank you