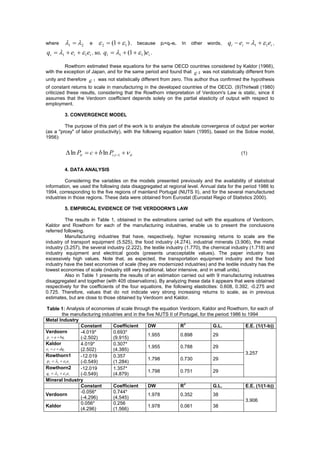
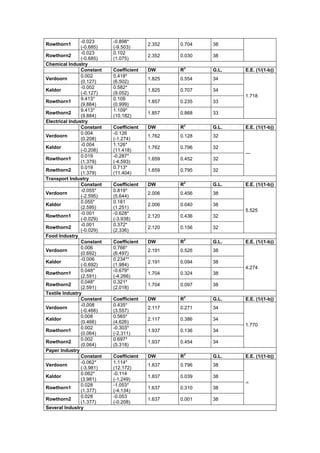
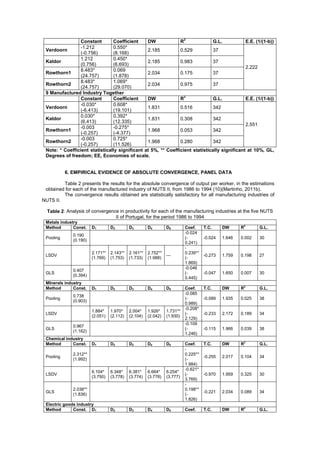
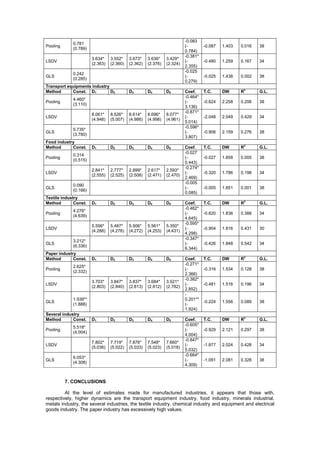
This document analyzes productivity convergence theories and Verdoorn's Law for manufactured industries in Portuguese regions from 1986 to 1994. It tests alternative specifications of Verdoorn's Law proposed by Kaldor and Rowthorn on panel data for five Portuguese regions. The results show varying degrees of increasing returns to scale across industries, with transportation and food having the highest and textiles the lowest. Testing an absolute convergence model, it finds the data provide some evidence supporting Verdoorn's Law and Kaldor's specifications, but not strong increasing returns to scale across all industries.