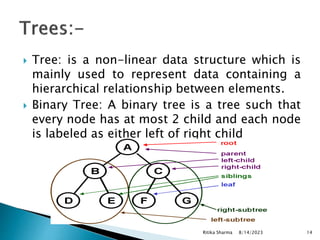
This document discusses data structures and algorithms. It defines a data structure as a way of organizing and storing data in a computer for efficient use. Different types of data structures are described, including arrays, stacks, queues, linked lists, trees and graphs. The document also defines an algorithm as a step-by-step plan to solve a computational problem and discusses analyzing algorithms to measure efficiency based on worst case, average case and best case running times. It describes the tradeoff between time and space complexity in algorithm design.

1. By:
Ritika Sharma
Assistant Professor
CSED, MAIT
MAU
8/14/2023 1
Ritika Sharma

2.  Data Structure . – A data structure is a
particular way of storing & organizing data in
a computer so that it can be used efficiently.
 A scheme for organizing related pieces of
information.
 Data Structure are generally based on the
ability of a computer to fetch and store data
at any place in its memory.
 A data str. is a group of data elements
grouped together under one name.
8/14/2023
Ritika Sharma 2

3.  Human requirement with computer are going
to complex day by day. To solve the complex
requirements in efficient way we need this
study.
 Provide fastest solution of human
requirements.
 Provide efficient solution of complex
problem.
– Space
– Time
8/14/2023
Ritika Sharma 3

4.  DBMS- ?
 Compiler Design-?
 Artificial Intelligence-?
 Operating Systems-?
 Network Analysis etc.
8/14/2023
Ritika Sharma 4

5.  Logical or mathematical description of the
structure.
 Implementation of structure on a computer
using different computer languages ( C, C++,
JAVA, pl-languages etc.)
 Quantitative analysis of the structure, which
includes determining the amount of memory
needed to store the structure and the time
required to process the structure.
(Complexity).
8/14/2023
Ritika Sharma 5

6. 8/14/2023
Ritika Sharma 6

7.  1. According to Nature of Size
i) Static Data Structure:- A data Structure is
said to be if we can store data up to a fix
number e.g., array.
ii) Dynamic Data Structure:- which allows the
programmer to change its size during program
execution to add or delete data.
 2. According to its Occurrence:-
i) Linear DS:- here, data is stored in
consecutive memory locations or in sequential
from, e.g., array, link-list, stack, queue..
8/14/2023
Ritika Sharma 7

8. ii) Non- Linear DS:- The data items are not
arranged in a sequential structure. Ex: Trees,
Graphs.
 3. Primitive or Non Primitive Data structures
i) Primitive:- these are the basic data Structures
and directly operated on the machines, e.g., int,
float, char, strings etc.
ii) Non-Primitive Data structures:- They are
derived from the primitive data str. They can be
grouped as homogeneous or heterogeneous. Ex:
Array, Linked list, trees, graphs .
8/14/2023
Ritika Sharma 8

9.  Creating:- declaration and initialization of data
str. and reserved memory location for data
elements
 Inserting:- Adding new records to the structure.
 Deleting:- removing records from the ds.
 Updating:- It changes the data values of the ds.
 Traversing:- Accessing each record of ds exactly
once.
 Searching:- finding records
 Sorting:- Arranging records
 Merging:- Combining records of two diffn DS.
8/14/2023
Ritika Sharma 9

10.  Array: is commonly used in computer
programming to mean a contiguous block of
memory locations, where each memory
location stores one fixed-length data item.
e.g. Array of Integers int a[10], Array of
Character char b[10]
8/14/2023
Ritika Sharma 10

11.  Stack: A stack is a data structure in which
items can be inserted only from one end and
get items back from the same end. There ,
the last item inserted into stack, is the the
first item to be taken out from the stack. In
short its also called Last in First out [LIFO].

8/14/2023
Ritika Sharma 11

12.  Queue: A queue is two ended data structure
in which items can be inserted from one end
and taken out from the other end. Therefore ,
the first item inserted into queue is the first
item to be taken out from the queue. This
property is called First in First out [FIFO].
8/14/2023
Ritika Sharma 12

13.  Linked List: Could alternately used to store
items. In linked list space to store items is
created as is needed and destroyed when
space no longer required to store items.
Hence linked list is a dynamic data structure
space acquire only when need.
8/14/2023
Ritika Sharma 13

14.  Tree: is a non-linear data structure which is
mainly used to represent data containing a
hierarchical relationship between elements.
 Binary Tree: A binary tree is a tree such that
every node has at most 2 child and each node
is labeled as either left of right child
8/14/2023
Ritika Sharma 14

15.  Graph: It is a set of items connected by edges.
Each item is called a vertex or node. Trees are
just like a special kinds of graphs. Graphs are
usually represented by G = (V, E), where V is the
set vertices and E is the set of Edges.
 Undirected Graph: A graph whose edges are
unordered pair of vertices. That is each edge
connects two vertices. In an undirected graph,
direction is not important, if the path is available,
it can be traversed in any direction
8/14/2023
Ritika Sharma 15

16.  Directed Graph: In directed graph a
directional edge connect two node/vertex. If
there is one edge from one vertex to other
then only this path can be followed
 Weighted Graph: A graph having a weight, or
number associated with each edge
8/14/2023
Ritika Sharma 16

17.  An Algorithm is a precise plan for performing
a sequence of actions to achieve the intended
purpose. Each action is drawn from a well-
understood selection on data.
 Defn:- An algorithm is a step by step finite
sequence of instructions, to solve a well
defined computational problems.
 Features:
 It should be free of ambiguity
 It should be precise.
 It should be efficient.
8/14/2023
Ritika Sharma 17

18.  After designing an algorithm, it has to be
checked and its correctness need to be
predicted; this is done by analyzing the
algorithm. Algorithm analysis means
measures the efficiency of the algorithm.
 A) Types of Analysis:
1. Worst case running time
2. Average case running time
3. Best case running time
8/14/2023
Ritika Sharma 18

19.  In the worst case analysis, we calculate upper
bound on running time of an algorithm. We
must know the case that causes maximum
number of operations to be executed.
 For example in Linear Search, the worst case
happens when the element to be searched (x)
is not present in the array. When x is not
present, the search() functions compares it
with all the elements of arr[] one by one.
Therefore, the worst case time complexity of
linear search would be “n”.
8/14/2023
Ritika Sharma 19

20.  In average case analysis, we take all possible
inputs and calculate computing time for all of
the inputs. Sum all the calculated values and
divide the sum by total number of inputs.
 For the linear search problem, let us assume
that all cases are uniformly
distributed (including the case of x not being
present in array). So we sum all the cases and
divide the sum by (n+1).
8/14/2023
Ritika Sharma 20

21.  In the best case analysis, we calculate lower
bound on running time of an algorithm. We
must know the case that causes minimum
number of operations to be executed. In the
linear search problem, the best case occurs
when x is present at the first location. The
number of operations in the best case is
constant (not dependent on n). So time
complexity in the best case would be Θ(1)
8/14/2023
Ritika Sharma 21

22.  It refers to a choice between algorithmic
solutions of a data processing problem that
allows one to decrease the running time of an
algorithm solution by increasing the space to
store data and vice versa.
 For example- we may have to choose a data
str. That requires a less memory and less
time to execute a problem.
8/14/2023
Ritika Sharma 22

23.  Time Complexity:- An algorithm A for a
problem P is said to have time complexity of
T(n) if the number of steps required to
complete its run for an input of size n is
always less than equal to T(n).
 Space Complexity:- An algorithm A for a
problem P is said to have space complexity of
S(n) if the number of bits required to
complete its run for an input of size n is
always less than equal to S(n).
8/14/2023
Ritika Sharma 23