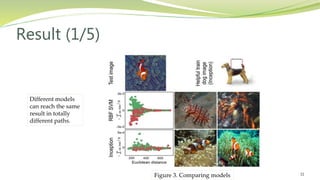
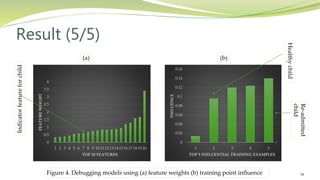
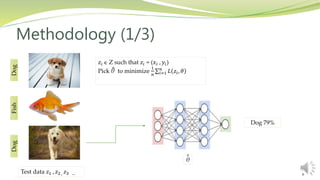
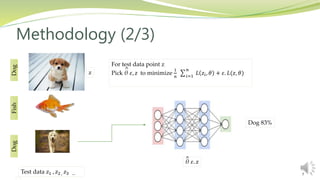
This document summarizes a research paper presented by Zabir Al Nazi at Khulna University of Engineering and Technology in Bangladesh. The paper discusses using influence functions to explain the predictions of black box machine learning models. It describes how influence functions can be used to identify influential training examples and features, debug models, and generate adversarial examples. The methodology scales the approach to large models using approximations of influence functions. Results show influence functions enabling analysis of different models that reach the same results through different paths, creation of adversarial examples, and debugging of a model that mispredicted hospital readmissions.

1. Pang Wei Koh
Stanford University,
Stanford, CA.
Percy Liang
Stanford University,
Stanford, CA.
Presented by,
Zabir Al Nazi
Roll : 1409016
Department of Electronics and Communication Engineering,
Khulna University of Engineering and Technology,
Khulna-9203, Bangladesh.
Mentored by,
Tasnim Azad Abir
Lecturer,
Department of Electronics and Communication Engineering,
Khulna University of Engineering and Technology,
Khulna-9203, Bangladesh.
Proceedings of the 34th International Conference on Machine Learning
1

2. Agenda
 Introduction
 Objectives/Research Questions
 Methodology
 Scaling Up
 Results
 Conclusion and Future Work
 Acknowledgements
2

3. Introduction (1/2)
Error(%)
Figure 1. ImageNet Large Scale Visual Recognition Challenge top 5 error
Human
ImageNetDataset
TeslaK80
GPU
+
3

4. Introduction (2/2)
Output
Benign (78%)
Acoustic Neuroma (3%)
Chordoma (11%)
Meningioma (8%)
Input
Figure 2. Black box prediction of Brain Cancer classification 4

5. Objectives/Research Questions
Given a high-accuracy black-box model and a prediction –
 Can we answer why did the model make this prediction?
Training Dataset
Prediction ?
Input
5

6. Methodology (1/3)
𝑧𝑖 є Z such that 𝑧𝑖 = (𝑥𝑖 , 𝑦𝑖)
Pick θ to minimize
1
𝑛 𝑖=1
𝑛
𝐿 𝑧𝑖, 𝜃^
Test data 𝑧1 , 𝑧2 , 𝑧3 …
DogFishDog
Dog 79%
θ
6

7. Methodology (2/3)
For test data point z
Pick θ 𝜀, 𝑧 to minimize
1
𝑛 𝑖=1
𝑛
𝐿 𝑧𝑖, 𝜃 + 𝜀. 𝐿(𝑧, 𝜃)
^
Test data 𝑧1 , 𝑧2 , 𝑧3 …
DogFishDog
Dog 83%
z
θ 𝜀. 𝑧
7

8. Methodology (3/3)
 Influence
 What is 𝐿 𝑧𝑡𝑒𝑠𝑡, θ 𝜀, 𝑧 − 𝐿 𝑧𝑡𝑒𝑠𝑡, θ ?
 How much the prediction changes for a single data point
(removing from test data)?
 But retraining for each z , 𝜀 is costly.
8

9. Scaling Up (1/3)
 Influence Function
 Robust Statistics, 1970
 Consider an estimator T which will act on a distribution F
 How much does T change if we perturb F?
9

10. Scaling Up (2/3)
 𝜃 𝜀, 𝑧 = arg minθ
1
𝑛 𝑖=1
𝑛
𝐿 𝑧𝑖, 𝜃 + 𝜀. 𝐿(𝑧, 𝜃)
 Influence of upweighting z on parameters 𝜃 is given by –
 𝐼 𝑢𝑝, 𝑙𝑜𝑠𝑠 =
𝜕𝐿(𝑧𝑡𝑒𝑠𝑡, 𝜃𝜀,𝑧)
𝜕 𝜀
= 𝛻𝜃 𝐿 𝑧𝑡𝑒𝑠𝑡 , 𝜃
𝑇
𝐻 𝜃
−1
𝛻𝜃 𝐿 𝑧 , 𝜃 [1]
 𝐻 𝜃 =
1
𝑛 𝑖=1
𝑛
𝛻𝜃
2 𝐿 𝑧𝑖, 𝜃
[1] Cook & Weisberg, 1982
10

11. Scaling Up (3/3)
 Don’t explicitly form 𝐻 𝜃
−1
, instead compute 𝐻 𝜃
−1
𝑣
𝑣 𝐻 𝜃 𝑣 𝐻 𝜃
−1
𝑣
Pearlmutter trick [1] CG [2]
Taylor [3]
[1] Pearlmutter, 1994
[2] Martens, 2010
[3] Agarwal, Bullins, 2016
11

12. Result (1/5)
Figure 3. Comparing models
Different models
can reach the same
result in totally
different paths.
12

13. Result (2/5)
 ML systems get their training data from outside world which is
vulnerable to attack
 Can we create adversarial training examples?
Dog (97%) Dog (98%) Dog (98%)
Dog(99%)
Dog(98%)
Label: Fish
13

14. Result (3/5)
 How easy it is to fool a machine learning model?
Fish (97%) Fish (93%) Fish (87%)
Fish(63%)
Fish(52%)
Label: Fish
14

15. Result (4/5)
 Debugging model errors: Why did a model make a wrong prediction?
 Case study: Hospital re-admission (20K patients, 127 features)
Healthy + re-admitted
adults
Healthy children
Re-admitted children
Original Modified
~20K ~20K
21 1
3 3
same
-20
same
15

16. Result (5/5)
0
0.5
1
1.5
2
2.5
3
3.5
4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
FEATUREWEIGHT
TOP 20 FEATURES
Indicatorfeatureforchild
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
1 2 3 4 5
INFLUENCE
TOP 5 INFLUENTIAL TRAINING EXAMPLES
Healthychild
Re-admitted
child
(a) (b)
Figure 4. Debugging models using (a) feature weights (b) training point influence 16

17. Conclusion and Future Work
 A new way of looking at high performing, complex, black box
models diagnostics
 Applications such as creating training set attacks, debugging,
fixing labels
 Underlying each of the applications is a common tool, simple
idea of Influence function
 Influence function assumes very small perturbation in the
model.
 Open problem – coming up with closed form with global
change in model
17

18. Acknowledgements
 The authors of the conference paper ‘Understanding Black-box
Predictions via Influence Functions’ Pang Wei Koh et al.
 I am grateful to my supervisor Tasnim Azad Abir sir, for his guidance
18

19. 19

20. 20