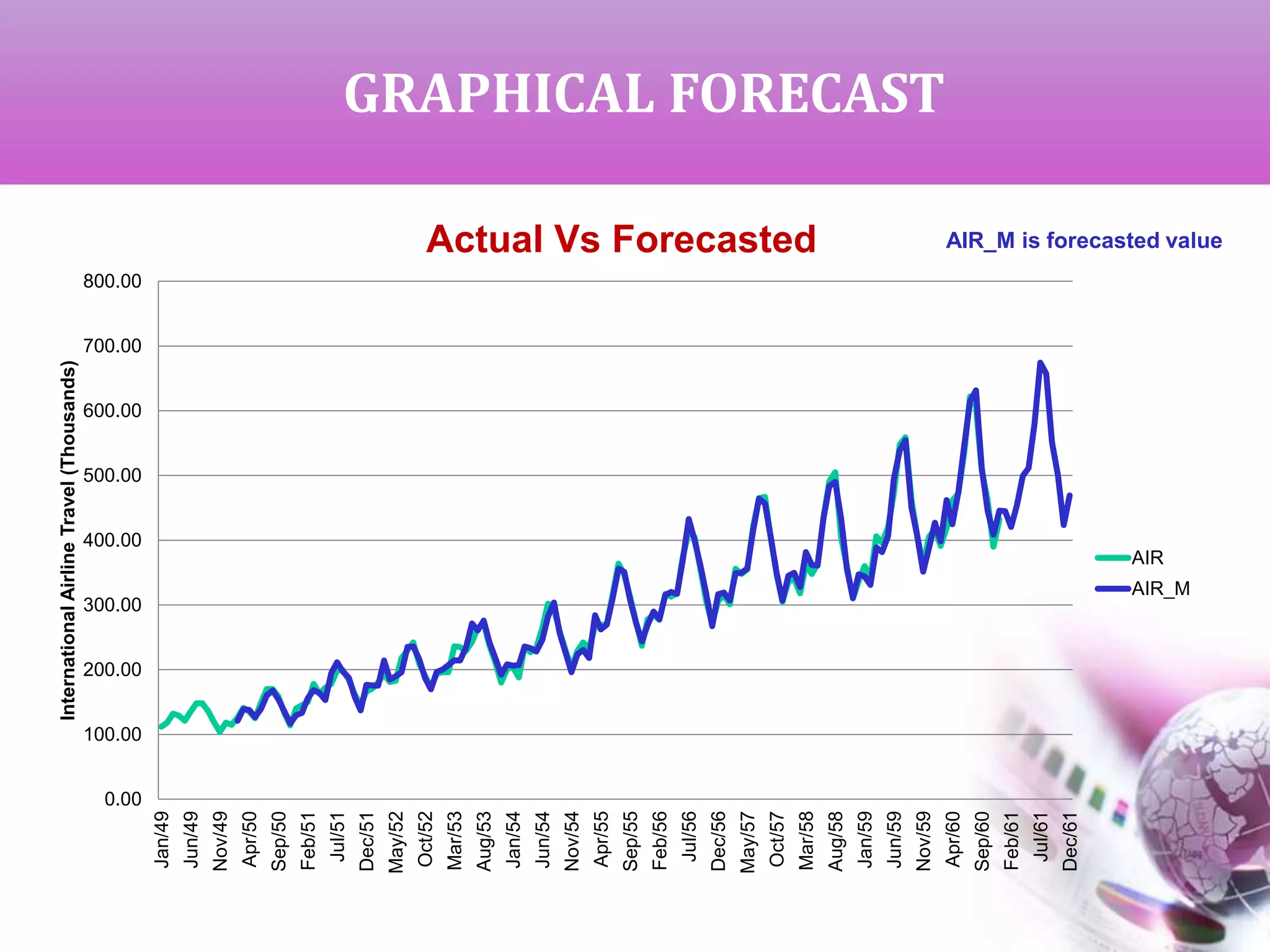
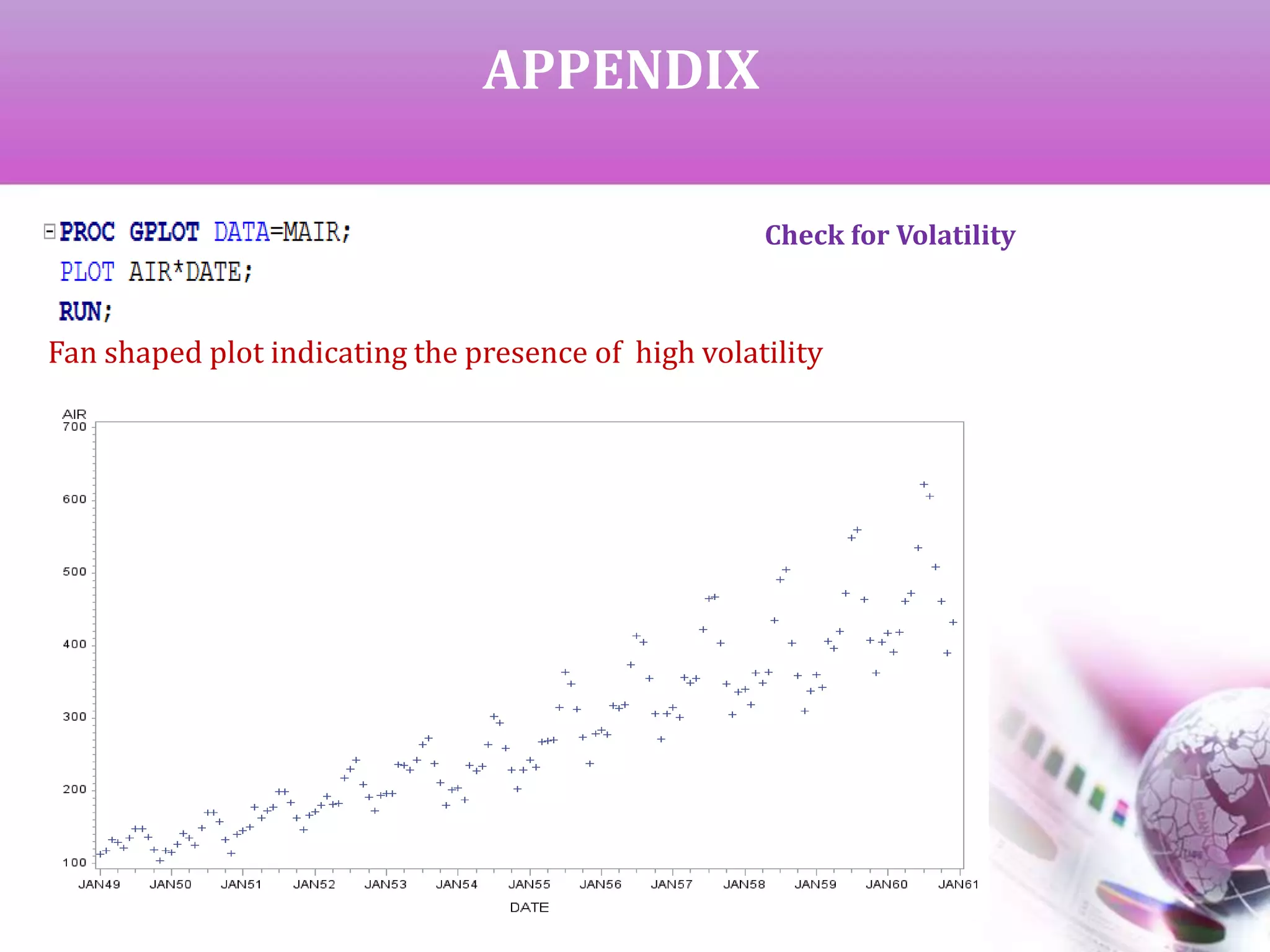
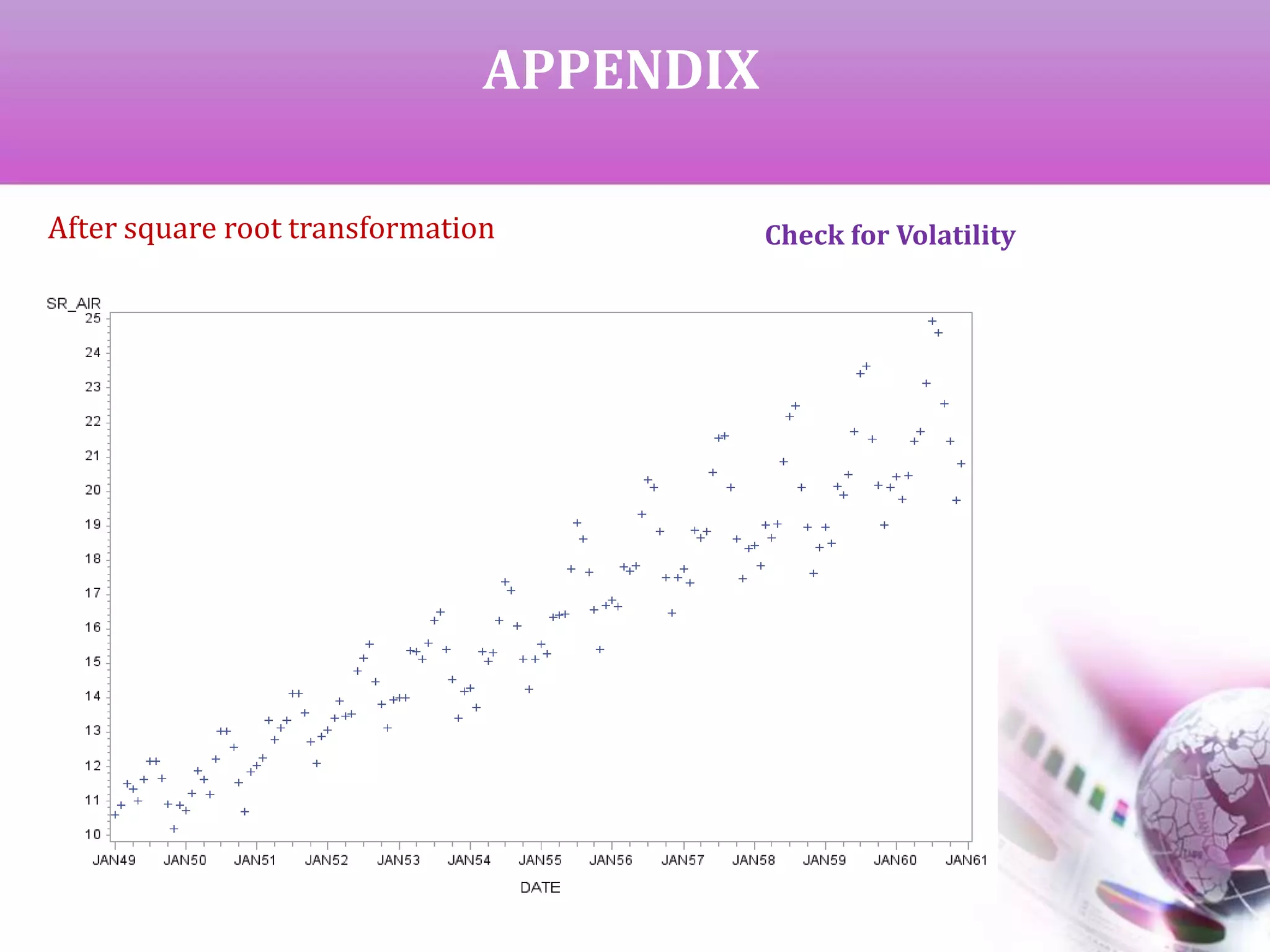
The document presents a study on time series analysis and forecasting of airline travel using the SAS dataset from January 1949 to December 1960. It details the methods for checking data volatility, non-stationarity, and seasonality, and describes the steps for model identification and estimation using the ARIMA framework. The final goal is to generate accurate forecasts for future airline travel based on the historical data analyzed.

1. TIME SERIES ANALYSIS
Modeling and Forecasting
Presented by
Vaibhav Jain (A13021)
Maruthi Nataraj (A13009)
Sunil Kumar (A13020)
Punit Kishore (A13011)
Arbind Kumar (A13003)

2. AGENDA
 Introduction
 Objective
 Data Preparation
 Check for Volatility
 Check for Non-Stationarity
 Check for Seasonality
 Model Identification and Estimation
 Forecasting
 Graphical Forecast

3. INTRODUCTION
 Time Series relates to values taken by a variable over time (such as daily sales
revenue, weekly orders, monthly overheads, yearly income) and tabulated or
plotted as chronologically ordered numbers or data points to yield valid
statistical inferences.
SL No Component Description
1 Trend Upward trend or Downward movement with little
fluctuation for a period of years
2 Seasonal Variation Short-term fluctuation in a time series which occur
periodically within a year.
3 Cyclical Variation Recurrent upward or downward with the period of
cycle is greater than a year.
4 Irregular Variation Random fluctuations which are short in duration
and erratic in nature .

4. OBJECTIVE
 In this study, we have to project the airline travel for the next 12 months .
Dataset Description
 The dataset used here is SASHELP.AIR which is Airline data and contains
two variables – DATE and AIR( labeled as International Airline Travel).
It contains the data from JAN 1949 to DEC 1960.

5. DATA PREPARATION
1.
• Check for Volatility
2.
• Check for Non-Stationarity
3.
• Check for Seasonality

6. DATA PREPARATION
Check for Volatility
 The plot of the data with time on horizontal axis and time
series on vertical axis provides an indication for volatility.
 A fan shaped or an inverted fan shaped plot shows high
volatility.
 For fan shaped plot, ‘log’ or ‘square root’ transformation is
used to reduce volatility ,while for inverted fan shaped plot ,’
exponential’ or ‘square’ transformation is used.

7. DATA PREPARATION
After log transformation ,with reduced volatility (constant variance)
Check for Volatility

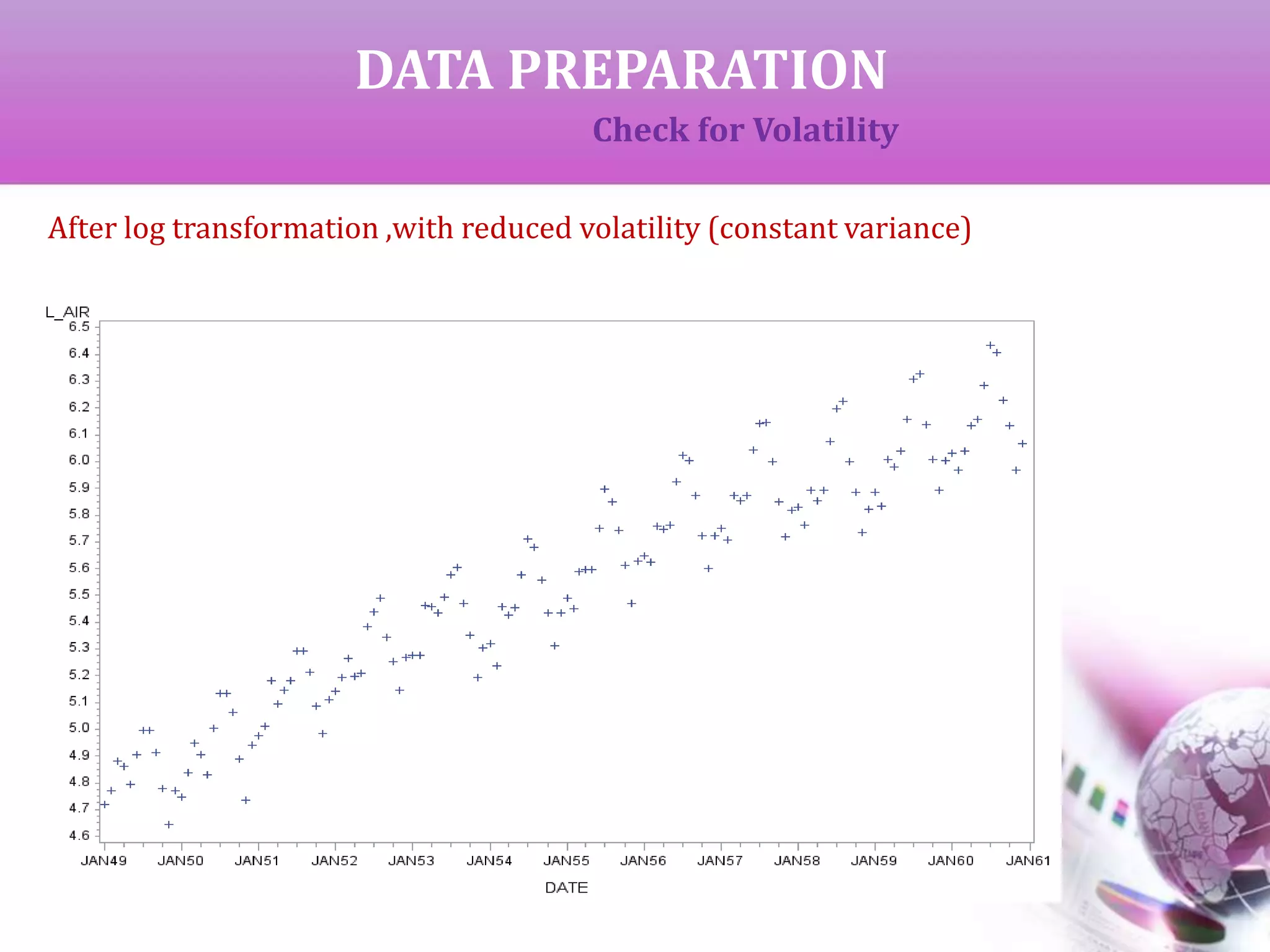
8. DATA PREPARATION
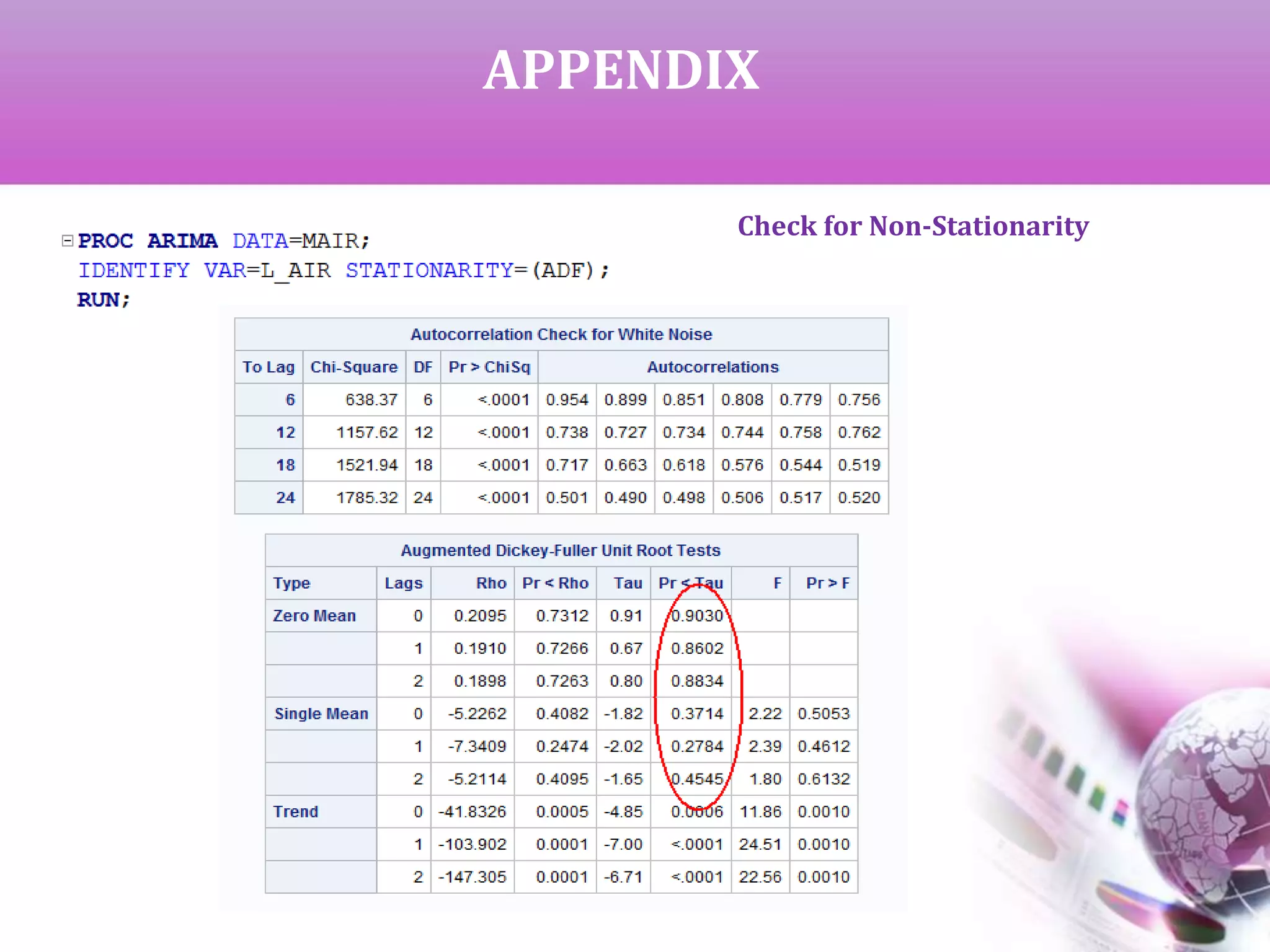
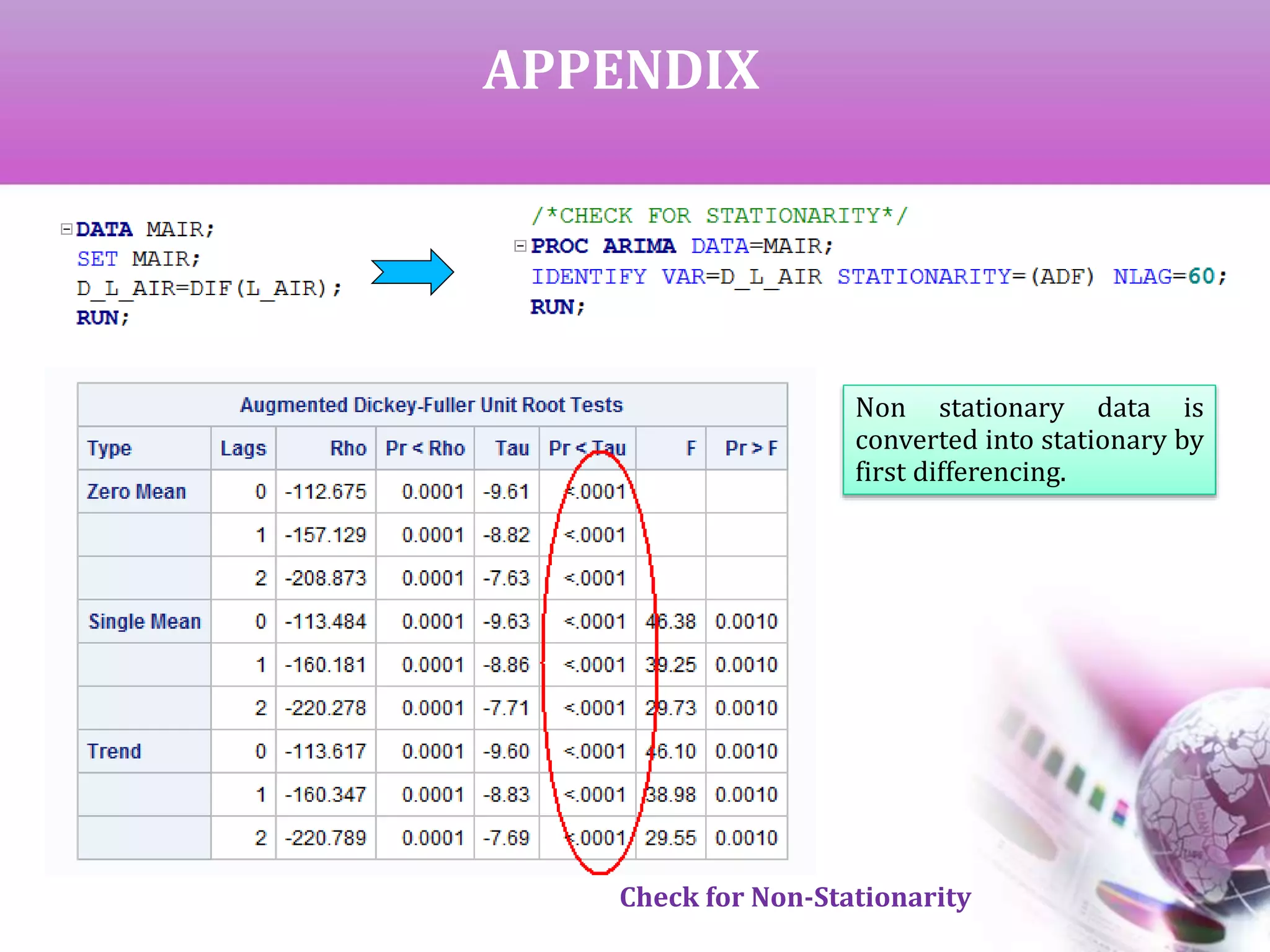
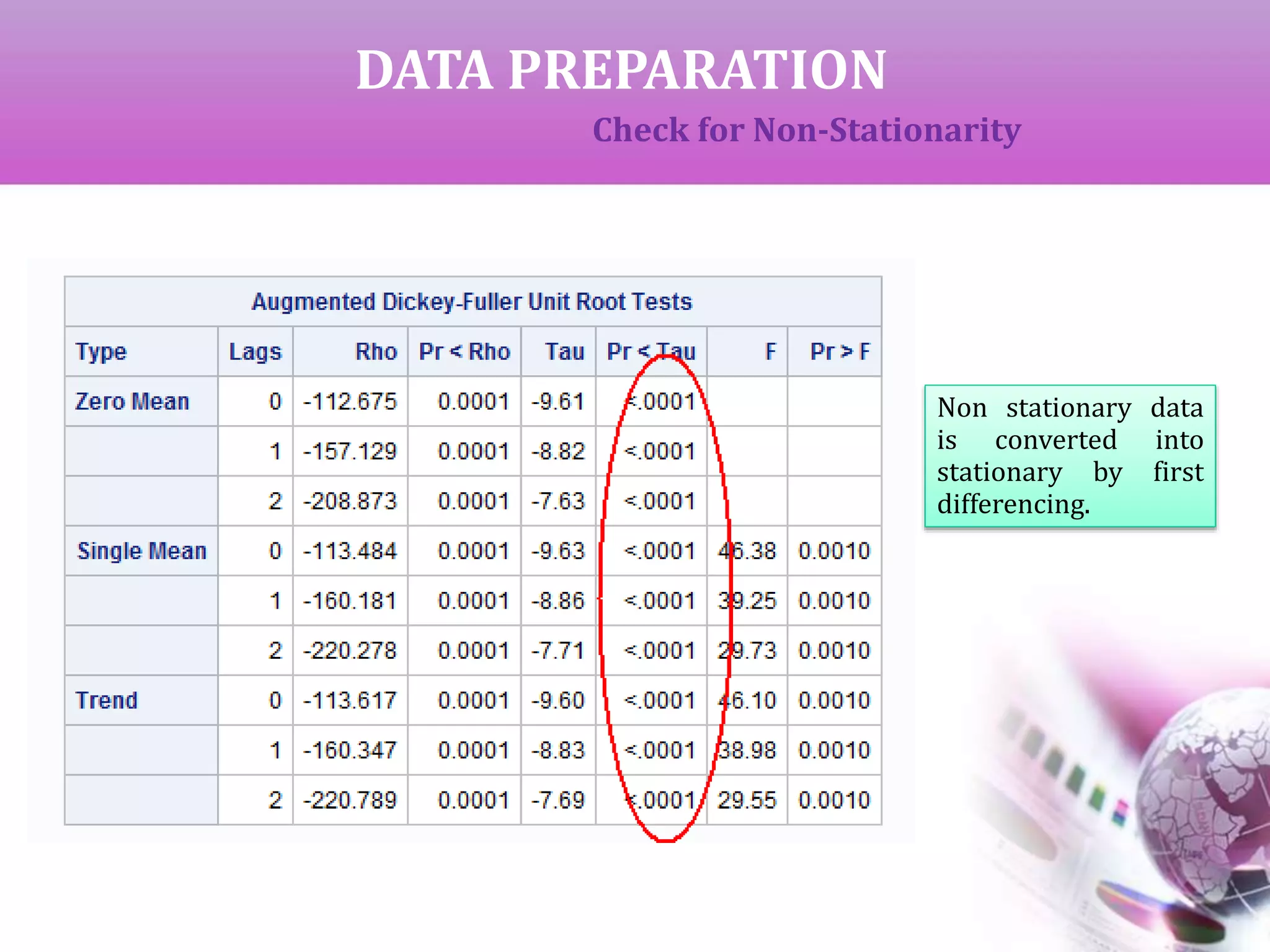
Check for Non-Stationarity
 If the data is completely random with no fixed pattern, it is called non-
stationary data and cannot be used for future forecasting. This is checked
by ‘Augmented Dickey-Fuller Unit Root Test’ (ADF).Here,
 H0 : Data is non-stationary
 If p < alpha, we reject H0 to claim that the data is stationary and
hence
can be used for forecasting.
 If p > alpha, we get non-stationary data which can be converted to
stationary by successive differencing.
 We can start with first difference (y[t]-y[t-1]) which can obtained using
DIF(L_AIR) or L_AIR(1).Similarly, if we need second difference, it is
DIF2(L_AIR) .

9. DATA PREPARATION
Check for Non-Stationarity
Non stationary data
is converted into
stationary by first
differencing.

10. DATA PREPARATION
ACF OUTPUT
Check for Non-Stationarity

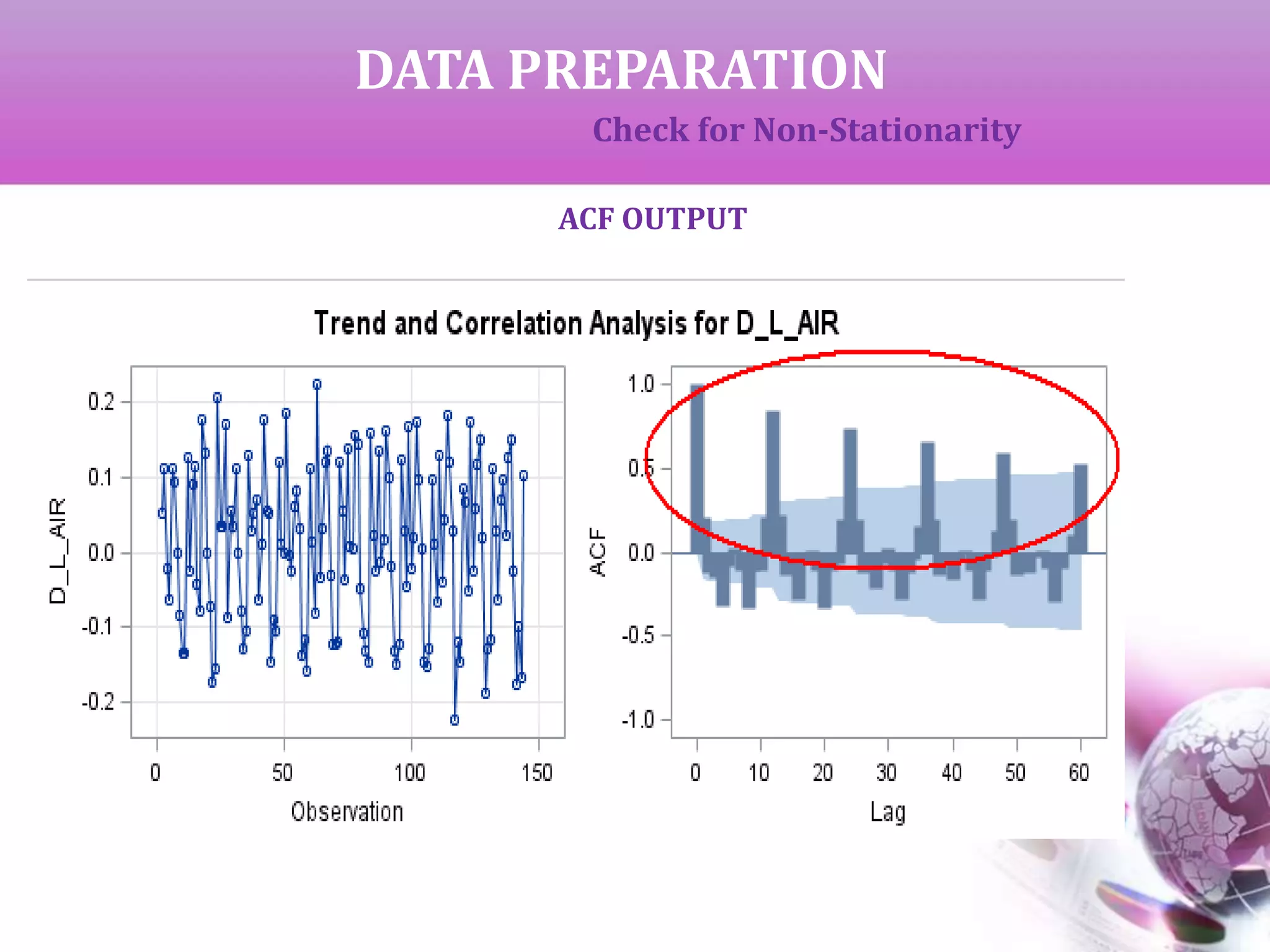
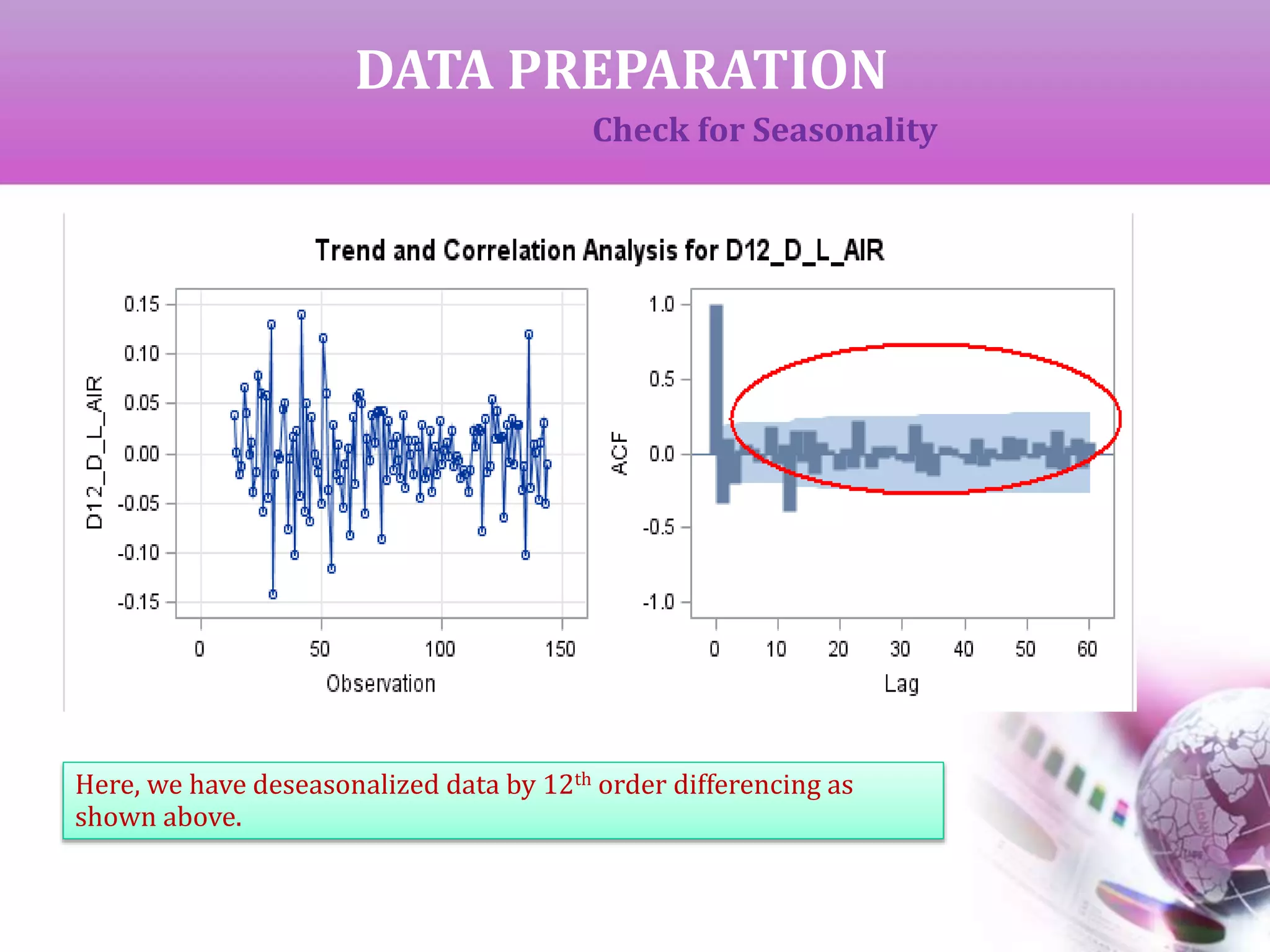
11. DATA PREPARATION
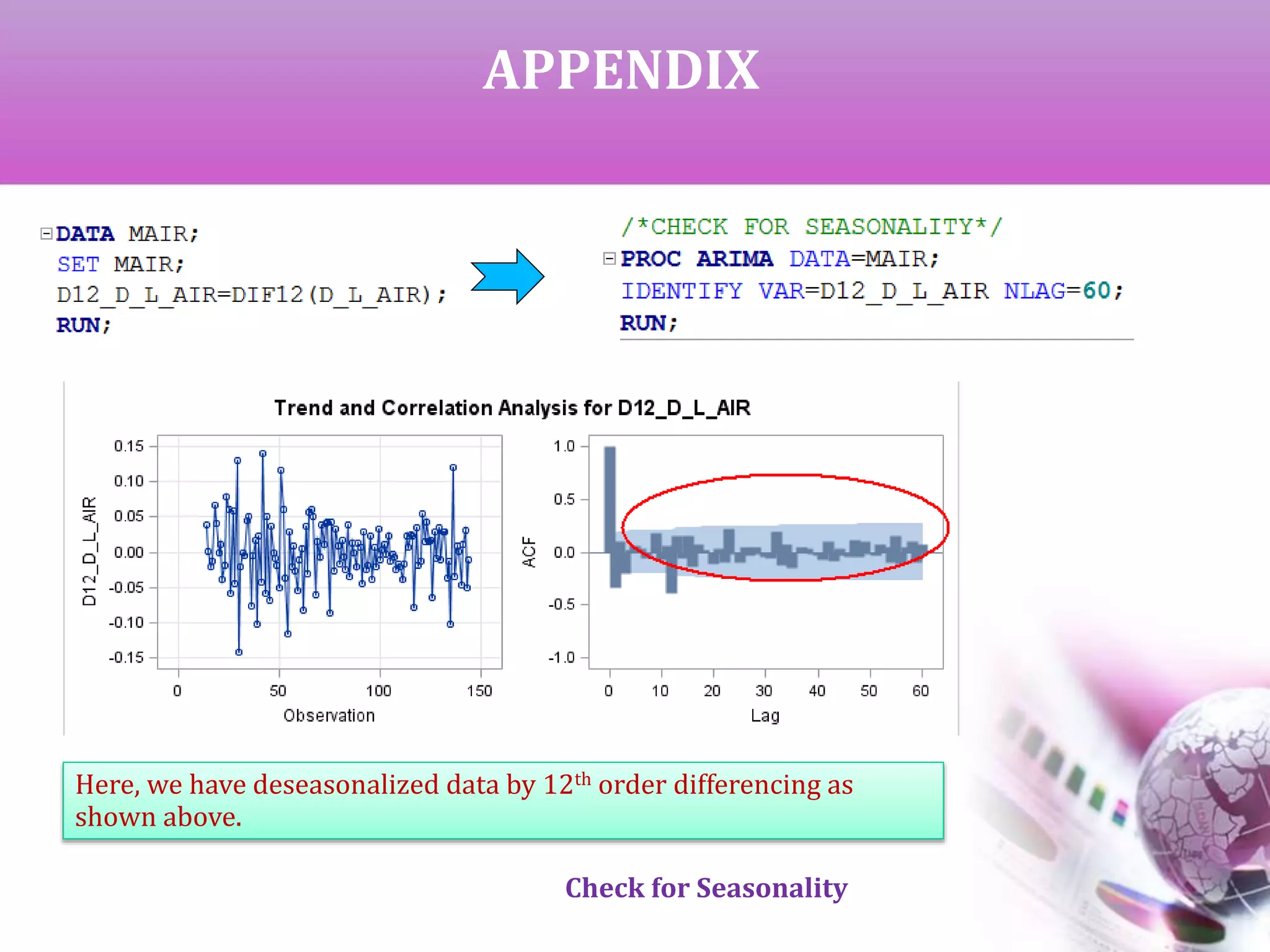
Check for Seasonality
 The Auto Correlation function (ACF) gives the correlation between
y[t]-y[t-s] where ‘s’ is the period of lag.
 If the ACF gives high values at fixed interval, that interval can be
considered as the period of seasonality. A differencing of same order
will deseasonalize the data.
 From the output of ACF it can be observed that the period of
seasonality is 12 years.

12. Here, we have deseasonalized data by 12th order differencing as
shown above.
DATA PREPARATION
Check for Seasonality

13. MODEL IDENTIFICATION
AND ESTIMATION
 Depending upon the number of future time points to be forecasted, we
set aside few of the most recent time points data as the validation
sample(V). The rest of the data which is the development sample(D), is
used to generate forecasts for different models.
 MINIC (Minimum Information Criteria) option under PROC ARIMA
generates the minimum BIC (Bayesian Information Criteria) Model after
exploring all the possible combinations of ‘p’ (Auto Regressive) and ‘q’
(Moving Average) lags from 0 to 5 (default).

14. MODEL IDENTIFICATION
AND ESTIMATION

15. MODEL IDENTIFICATION
AND ESTIMATION
 By observation, we can see that the minimum of the matrix is the
value -6.3503 corresponding to AR 3 and MA 0 location(i.e. p=3 & q=0).
 We consider all the models in the neighborhood of this model and for
each of them generate AIC (Akaike Information Criteria) and SBC
(Schwartz Bayesian Criteria) and calculate the average of them.
 We select the top 6-7 models based on relatively lower value of the
average and for each of them generate forecasts.

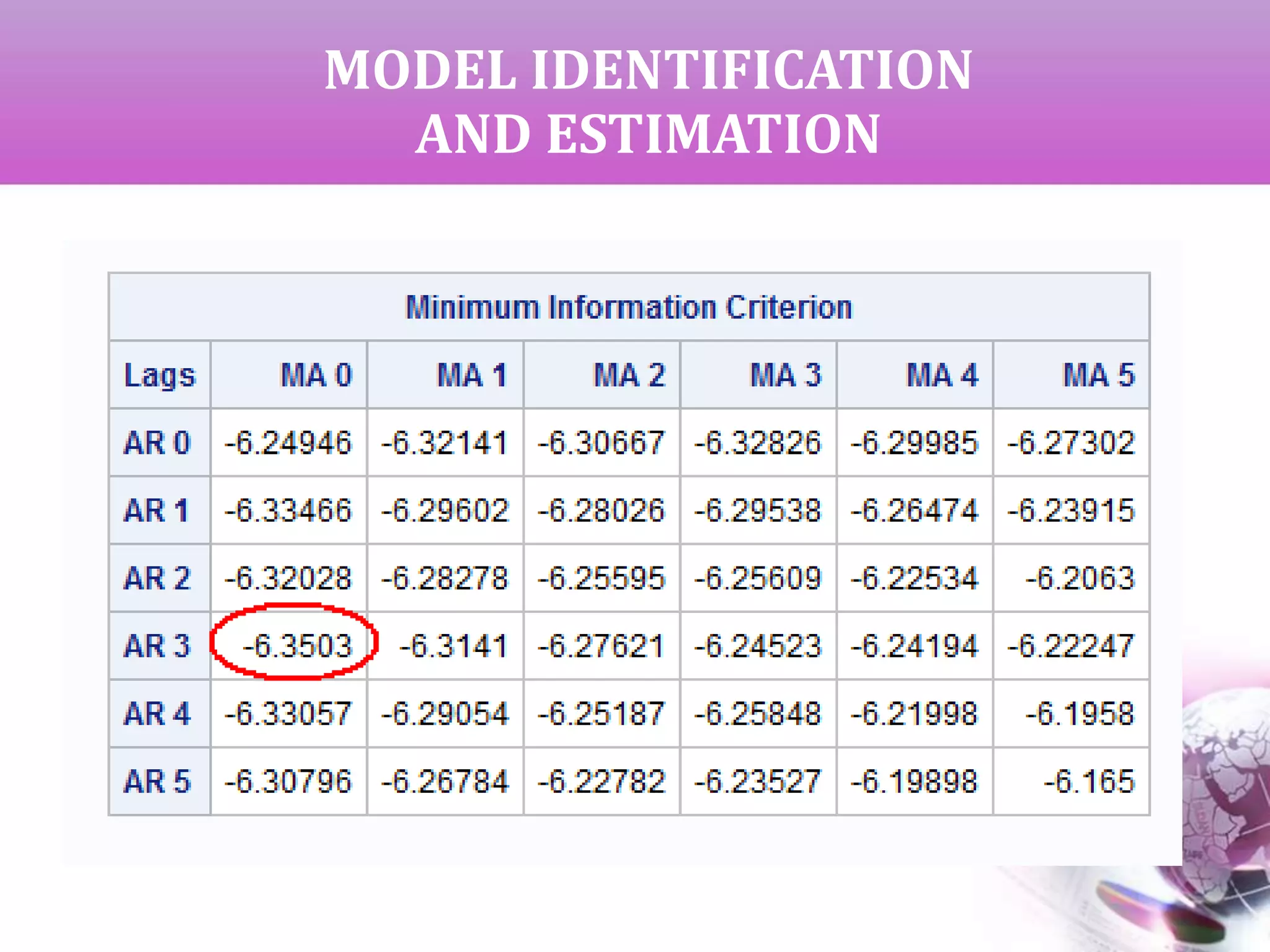
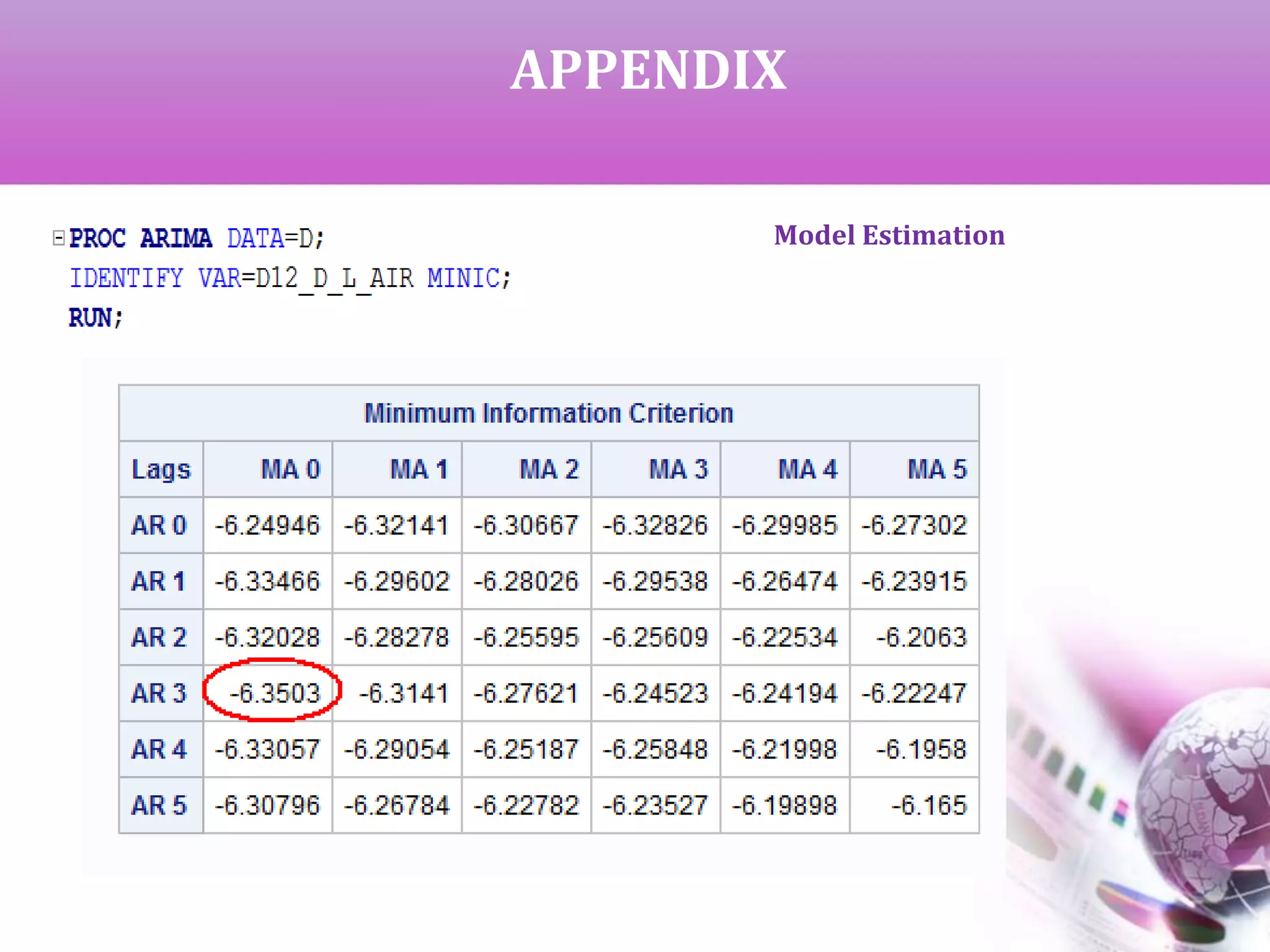
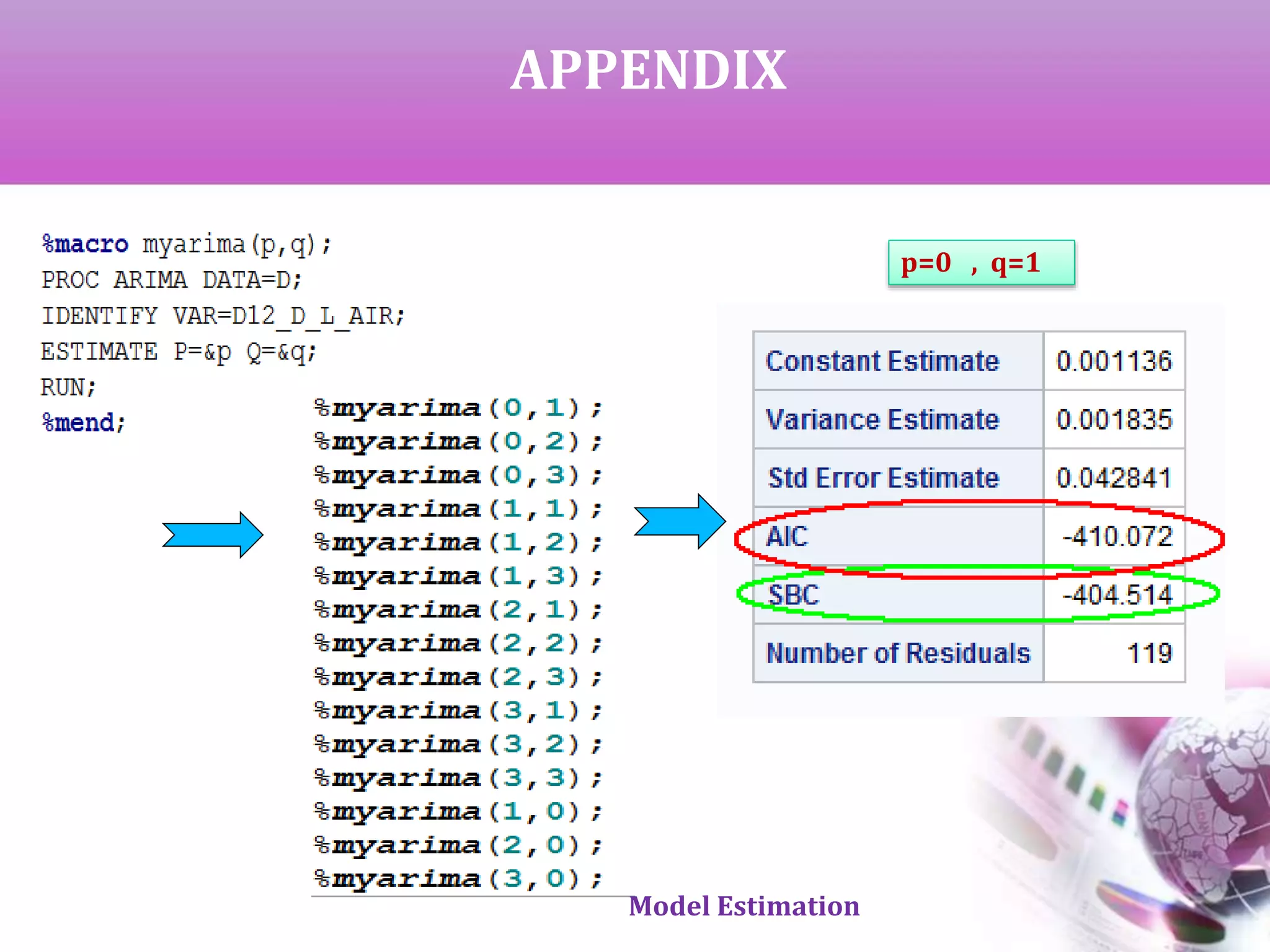
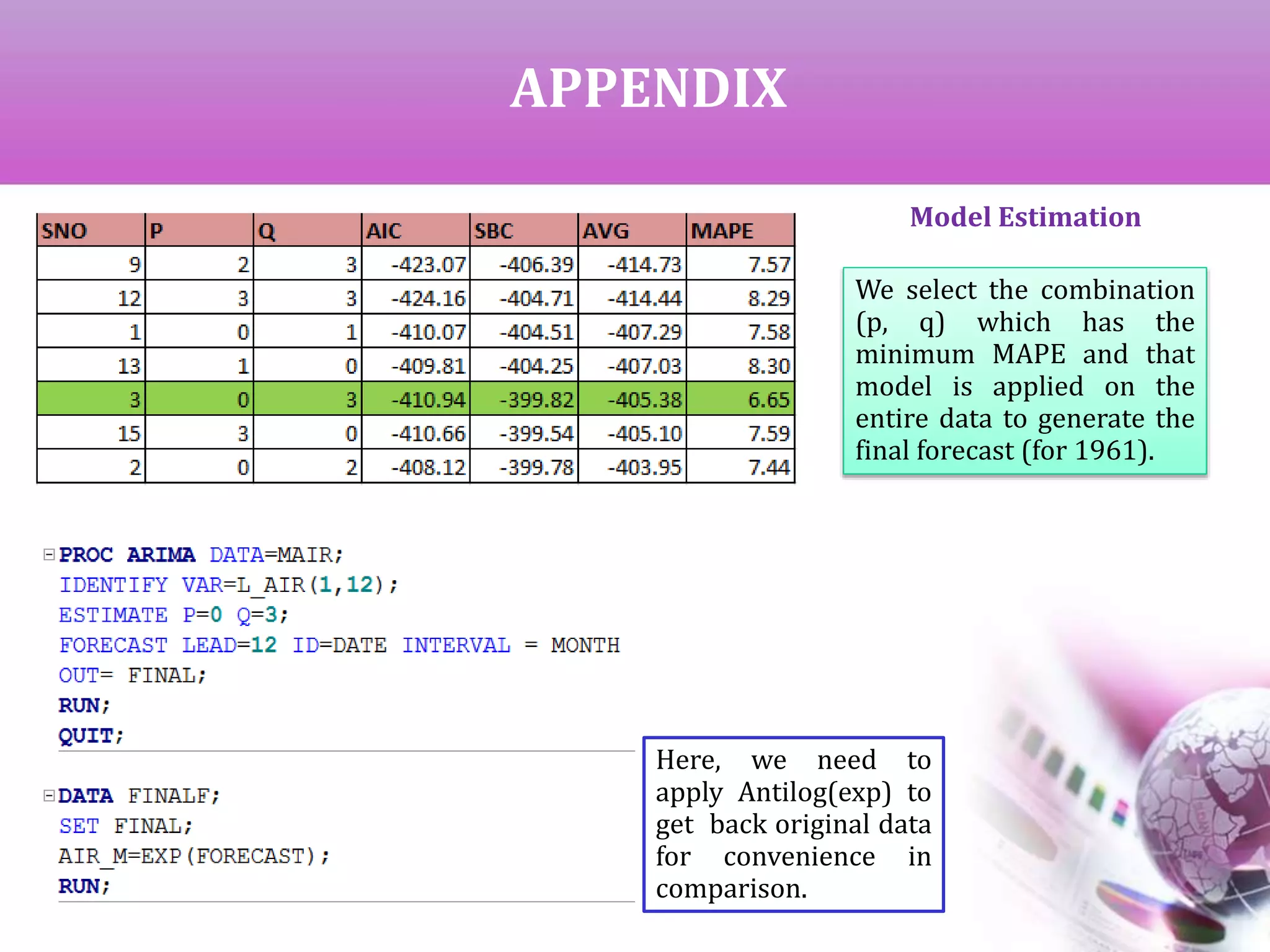
16. MODEL IDENTIFICATION
AND ESTIMATION
AIC & SBC for all the neighborhood
models [ (0,1) to (3,3)]
Top 7 models based on lower
average value
Model Estimation

17. FORECASTING
 Forecasts are generated using the FORECAST option in PROC
ARIMA.
 The forecasts generated (for 1960 in this case) for each combination
selected from AIC & SBC are separately compared with the actual
values of the same time point stored in the validation dataset (V) and
‘MAPE’ (Mean Absolute Percentage Error) is calculated.

18. FORECASTING
Forecasted Data

19. GRAPHICAL FORECAST
0.00
100.00
200.00
300.00
400.00
500.00
600.00
700.00
800.00
Jan/49
Jun/49
Nov/49
Apr/50
Sep/50
Feb/51
Jul/51
Dec/51
May/52
Oct/52
Mar/53
Aug/53
Jan/54
Jun/54
Nov/54
Apr/55
Sep/55
Feb/56
Jul/56
Dec/56
May/57
Oct/57
Mar/58
Aug/58
Jan/59
Jun/59
Nov/59
Apr/60
Sep/60
Feb/61
Jul/61
Dec/61
InternationalAirlineTravel(Thousands)
Actual Vs Forecasted
AIR
AIR_M
AIR_M is forecasted value

20. APPENDIX
Check for Volatility
Fan shaped plot indicating the presence of high volatility

21. APPENDIX
After square root transformation Check for Volatility

22. APPENDIX
Check for Non-Stationarity

23. APPENDIX
Non stationary data is
converted into stationary by
first differencing.
Check for Non-Stationarity

24. Here, we have deseasonalized data by 12th order differencing as
shown above.
APPENDIX
Check for Seasonality

25. APPENDIX
Model Estimation

26. APPENDIX
p=0 , q=1
Model Estimation

27. APPENDIX
 Here,
LEAD = No of future time points to forecast
ID = Name of time variable
INTERVAL = Unit of time variable
OUT = Name of the output file which saves the forecast
Forecasting

28. APPENDIX
p=2 , q=3
Forecasting

29. APPENDIX
We select the combination
(p, q) which has the
minimum MAPE and that
model is applied on the
entire data to generate the
final forecast (for 1961).
Here, we need to
apply Antilog(exp) to
get back original data
for convenience in
comparison.
Model Estimation

30. Thank You