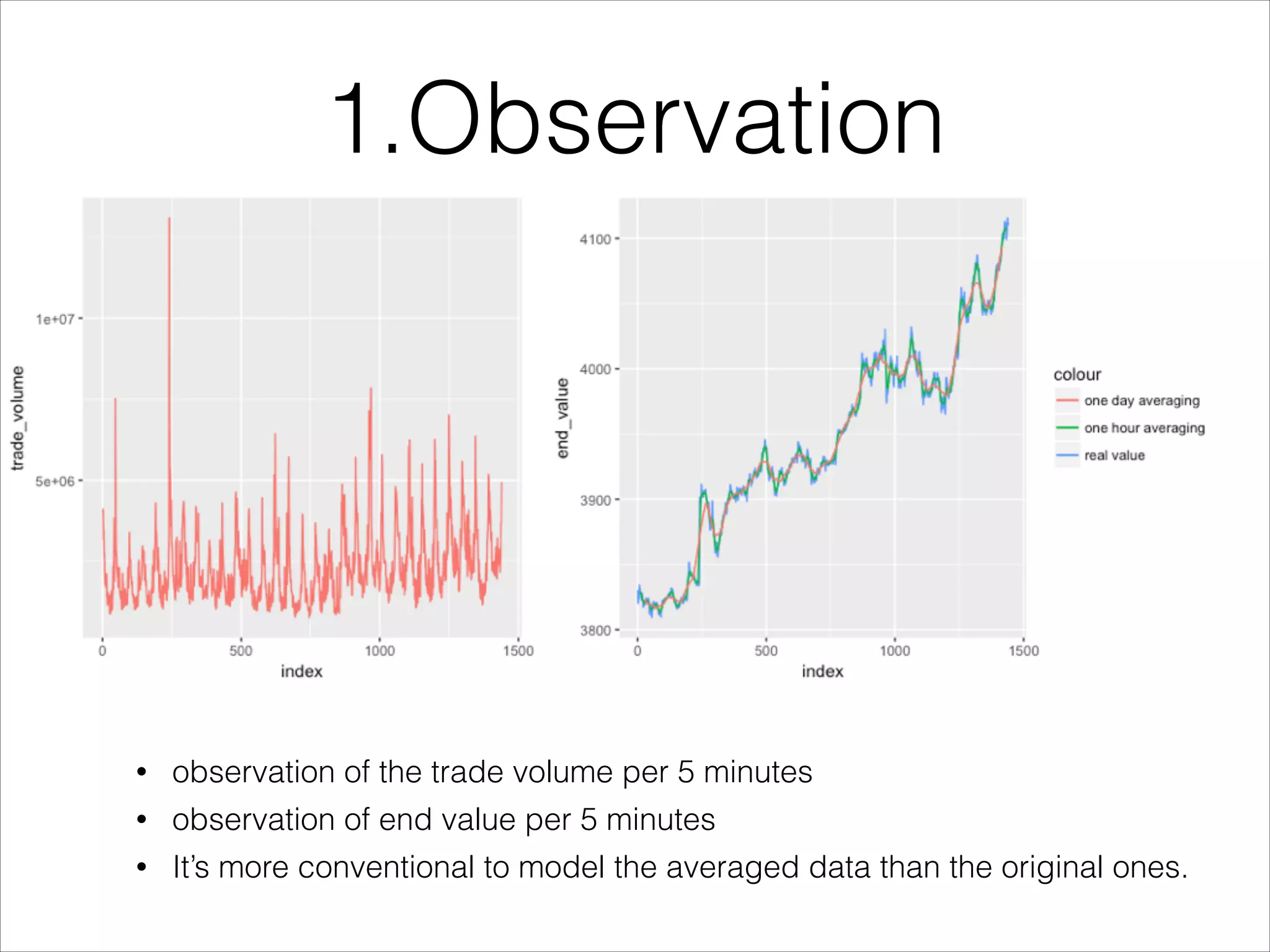
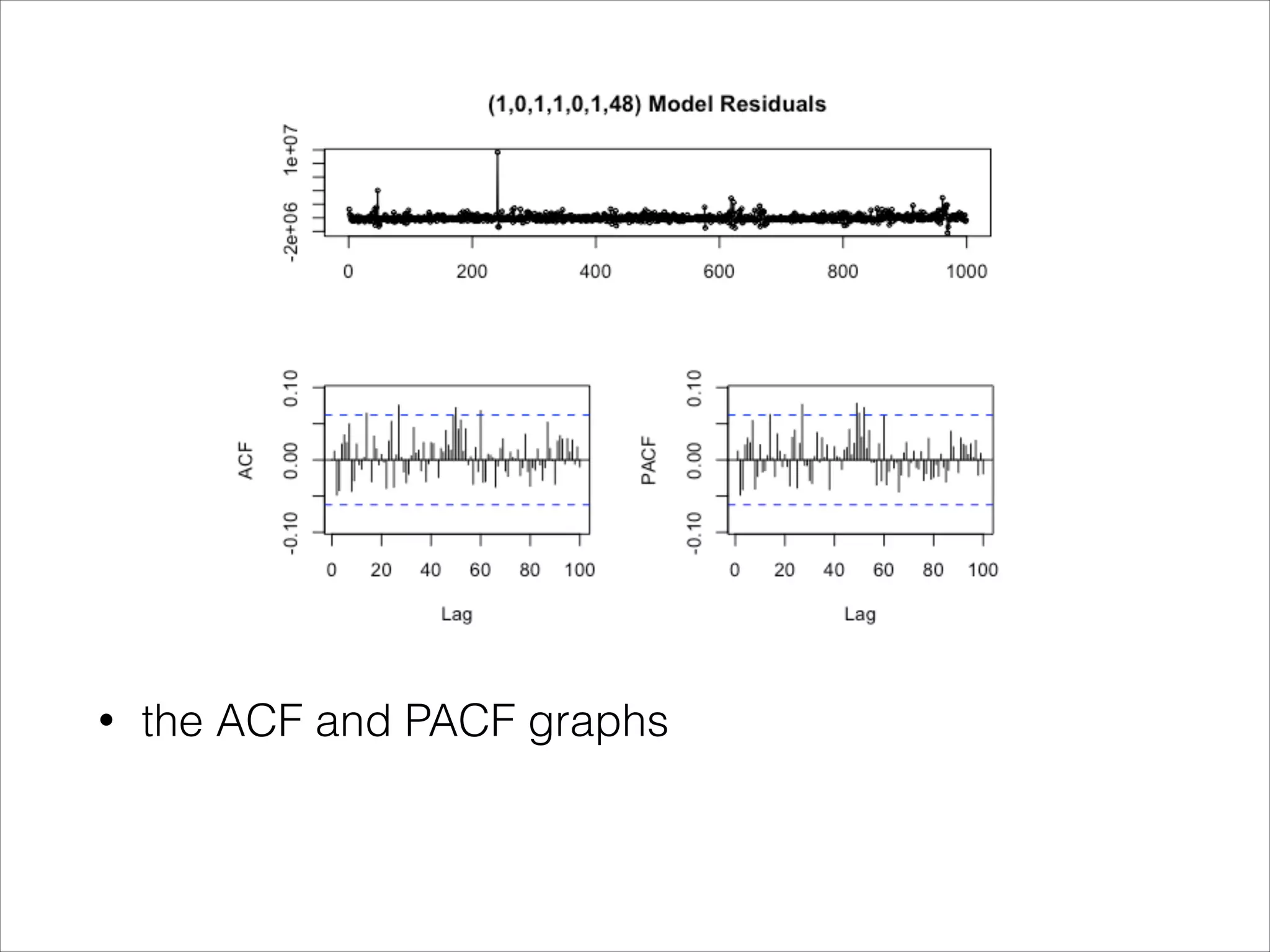
This document discusses autoregressive models for financial time series analysis. It introduces autoregressive (AR) and moving average (MA) processes. The autoregressive integrated moving average (ARIMA) model is presented as a way to fit time series data that accounts for correlation between observations. The document outlines the Box-Jenkins methodology for identifying and fitting an ARIMA model to time series data, including checking for stationarity, identifying orders using autocorrelation and partial autocorrelation functions, and selecting the best model. It applies this process to Shanghai Stock Exchange index data, finding that an ARIMA(48,1,0) model provided the best fit.

1. Autoregressive model
in financial time series
Mines ParisTech
Xiangnan YUE

2. Introduction
• Data visualization: the historical HS300 index from
2017.9 to 2017.11

3. Introduction
• In a case where no correlation is presented, it’s
called the white noise. (w(t)..)

4. Introduction
• Moving-average and autoregression are two ways
to introduce correlation and smoothness
• use 1/20 for [w(t-9),..,w(t),..,w(t +10)]

5. • autoregression
• x(t) = x(t-1) - 0.9x(t-2) + w(t)

6. Introduction
• Before using autoregression, the auto-correlation
and cross-correlation have to be checked.
• Auto-correlation is the relation between x(t+k) and
x(t), which is of the same time series.
• ACF(k) = cov(X(t+k), X(t)) / cov(X(t), X(t))
• cross-correlation is the relation between two time
series {x(n)} and {y(n)}

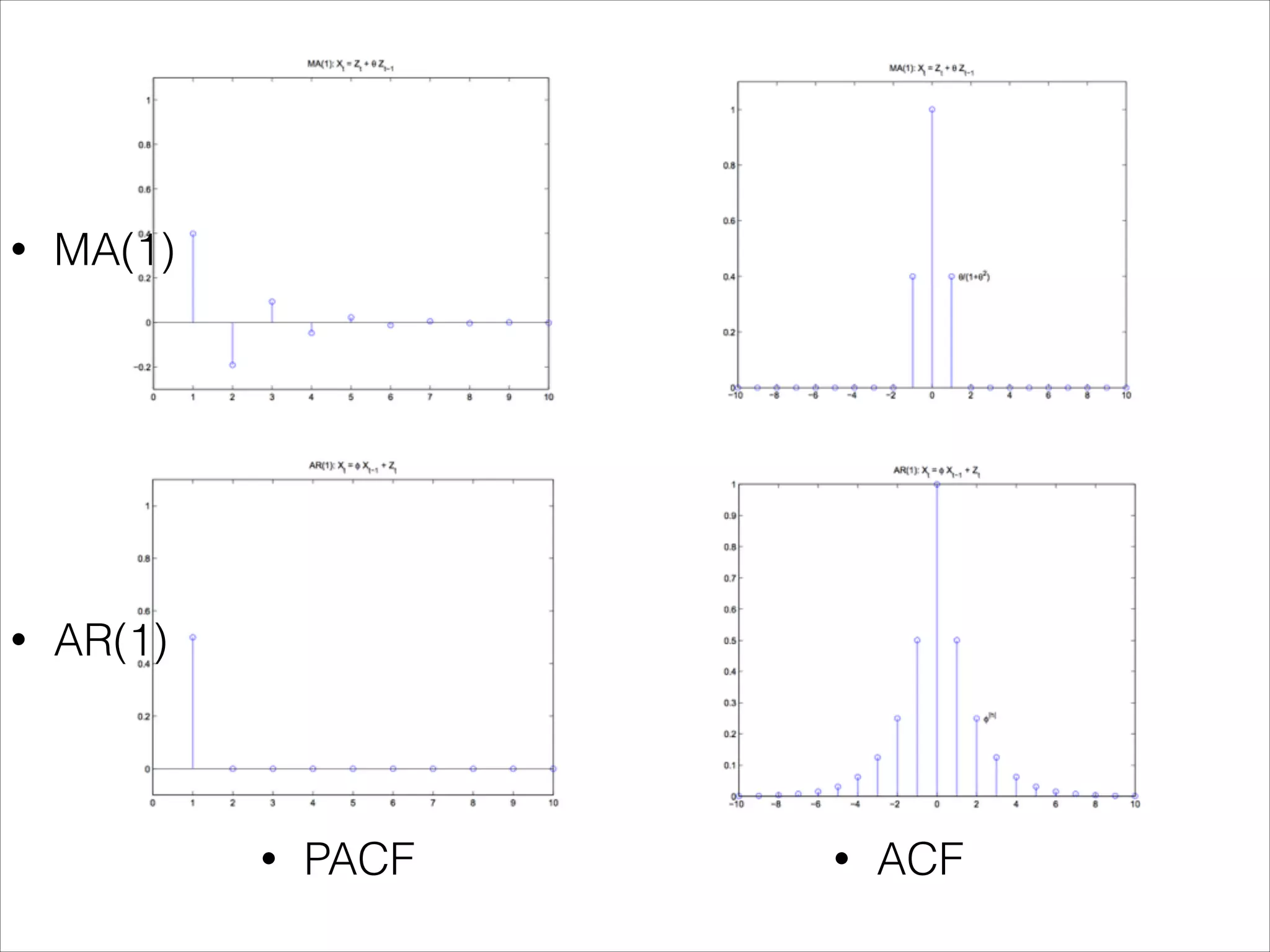
7. Introduction
• sometimes we see also the PACF, which is used to
remove the influence of intermedia variables.
• for example phi(h) is defined as
• If we remember that E[X(h)|X(h-1)] can be seen as the
projection of X(h) to the X(h-1) plane, this PACF(h) can be
explained in the following graph

8. • MA(1)
• AR(1)
• PACF • ACF

9. Introduction
• Yet with only one realization at each time t, to check
cov(x(t), x(t-k)) becomes feasible if we have the
weak stationary assumption.
• Weak stationary demands that
• the mean function E[X(t)]
• the auto-covariance function Cov(X(t+k), X(t))
• stay the same for different t.

10. Introduction
• Under classical linear model, Y = AX, independent
variables cannot be strongly correlated (otherwise,
it poses the problem of multi-linearity).
• This is not our case in time series (as shown by
ACF, variables at different time lags are strongly
correlated), where we introduce the ARIMA.

11. MA and AR process
• MA(q), which can be written as
• X(t) = W(t) + a1 * W(t-1) + … + ak * W(t-q), where
{W(t)} are white noises.
• AR(p), which can be written as

12. Fitting ARIMA to time series (R)
• The process of fitting ARIMA is referred to Box-
Jenkins method
• three orders (p, d, q) have to be decided for model.
• p: AR(p), number of lags used in the model.
• d: I(d), the order of differencing
• q: MA(q) combination of previous error terms.

13. 0.Get Data
• SHA300 Index
• data source
• http://quote.eastmoney.com/zs000300.html

14. 1.Observation
• observation of the trade volume per 5 minutes
• observation of end value per 5 minutes
• It’s more conventional to model the averaged data than the original ones.

15. 2. Decomposition
• One important thing is to discover the seasonality,
trend. In our 5-minute data, no special seasonality
has been found.
• For the trend and stationarity test, we pass directly
to the check of stationarity.

16. 3. Stationarity
• Fitting ARIMA requires time series to be stationary,
or weak stationary. (which is, the first and second
moment stay constant for the same time interval)
• Checking stationarity can be done by The
Augmented Dickey-Fuller (ADF) test. Null
assumption is the time series are not stationary.
• Before the test, it is clear from the graph that there is
some trend, so we have a reasonable guess that the
time series are not stable (a trend with time t exits)

17. 3. Stationarity - cont.
• the result of ADF test is as below, a large p-value (or
a less negative Dicky-Fuller value) cannot reject the
assumption, and we conclude that the time series
contain some trend.

18. 3. Stationarity - cont.
• to remove the trend effect of our time series, we take
the one-order difference between X(t) and X(t-1)
• this time, results show that we can reject the H0
assumption that stationarity doesn't exists.
• so we have reason to believe difference order d = 1

19. 4. Find orders of ARIMA
• Define z(t) = X(t) - X(t-1)
• Use ACF and PACF graph
• Focus on the spike of the ACF and PACF
• In this graph, we found
that the z(t) is auto-
correlated at lag 1 and 40
• PACF shows a significant
spike at lag 1 and 40
• so try p=q=1, 40, 48

20. 4. Find orders of ARIMA - cont.
• Other methods exist and needs to compare between
the models
• Criteria:
• Akaike Information Criteria (AIC)
• Baysian Information Criteria (BIC)
• Comparison: Minimise the AIC and BIC (lost infos.)
• Instead of trying models ourselves, R offers a
function auto.arima() to do this from scratch, yet this
does not always return a best forecast
• It’s often required to select from by experience.

21. • an experience table for choosing order p and q.

22. 4. Find orders of ARIMA - cont.
• auto.arima function suggests:
• X(t) - X(t-1) = 0.1950 + 0.0753*X(t-1) + e(t)
• yet ACF shows that some correlation between the residuals with
interval = 40 and 48 is not reflected

23. 4. Find orders of ARIMA - cont.
• try ARIMA(48, 1, 0) and ARIMA(1,1,48) … and look
at the correlation graph of ACF and PACF
• forecast by back-test

24. • the HS300 may behave more like random walking…
• yet our ARIMA(48, 1, 0) is only good for predicting about 50 * 5min,
• the further prediction is based on our previous predictions and is less exact.

25. 5. what to do next — the art
• Some time series are easier to predict as they contain regular
patterns. An example is the volume of trade
• yet the rule for adjusting the order of ARIMA is quite complicate,
and demand experiences, refer to literatures.
• http://people.duke.edu/~rnau/411arim3.htm#plots

26. • the ACF and PACF graphs

27. • at the beginning, it indicates a seasonal model.

28. • https://www.esat.kuleuven.be/sista/lssvmlab/
tutorial/node23.html
• https://onlinecourses.science.psu.edu/stat510/
node/67
• https://people.duke.edu/~rnau/seasarim.htm
• https://www.datascience.com/blog/introduction-to-
forecasting-with-arima-in-r-learn-data-science-
tutorials

29. To go further
• Stochastic models (Black-Scholes)
• ANN, Bayesian Learning …
• Reinforcement Learning, Recurrent Neural
Network…