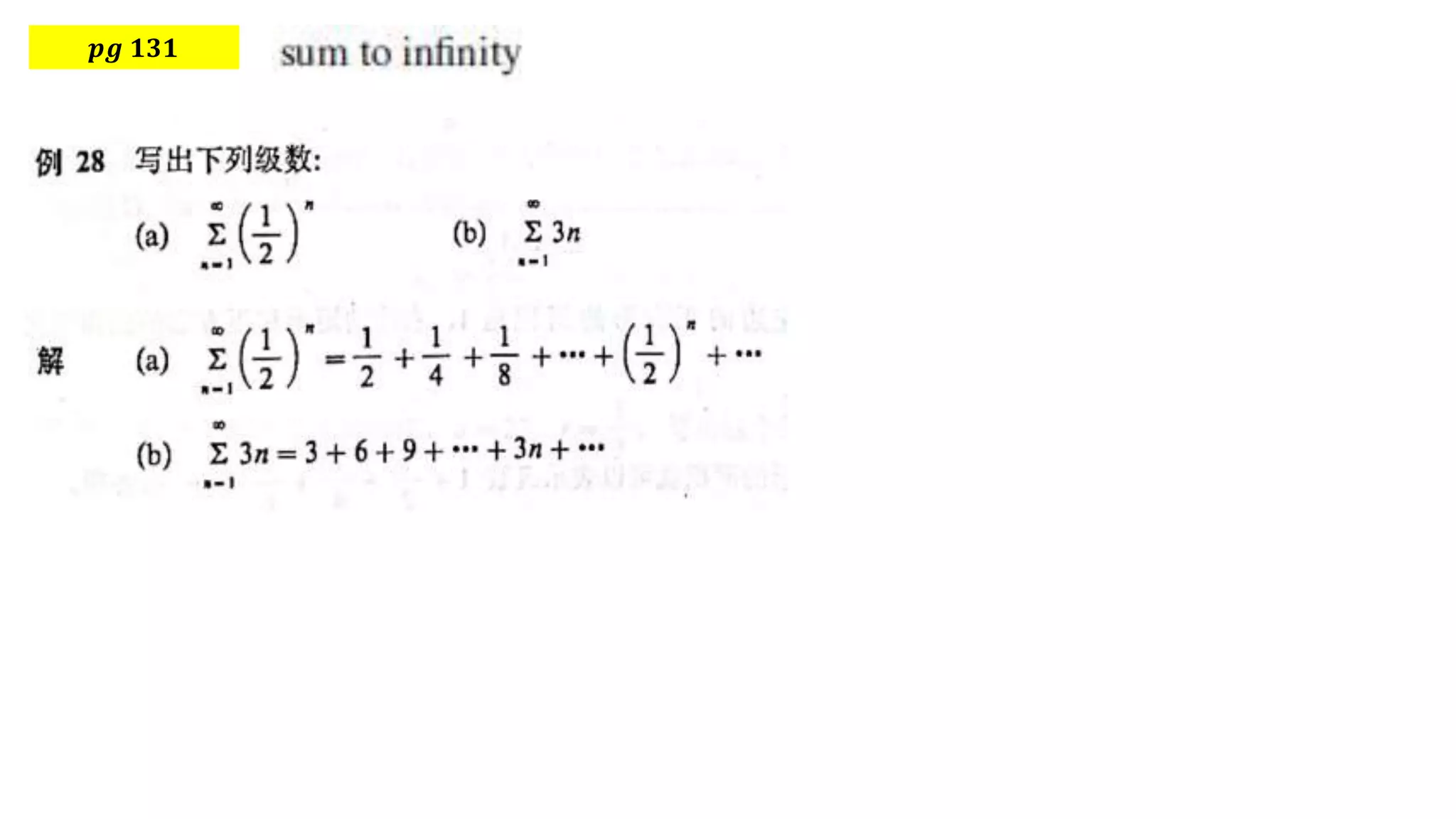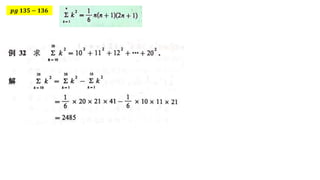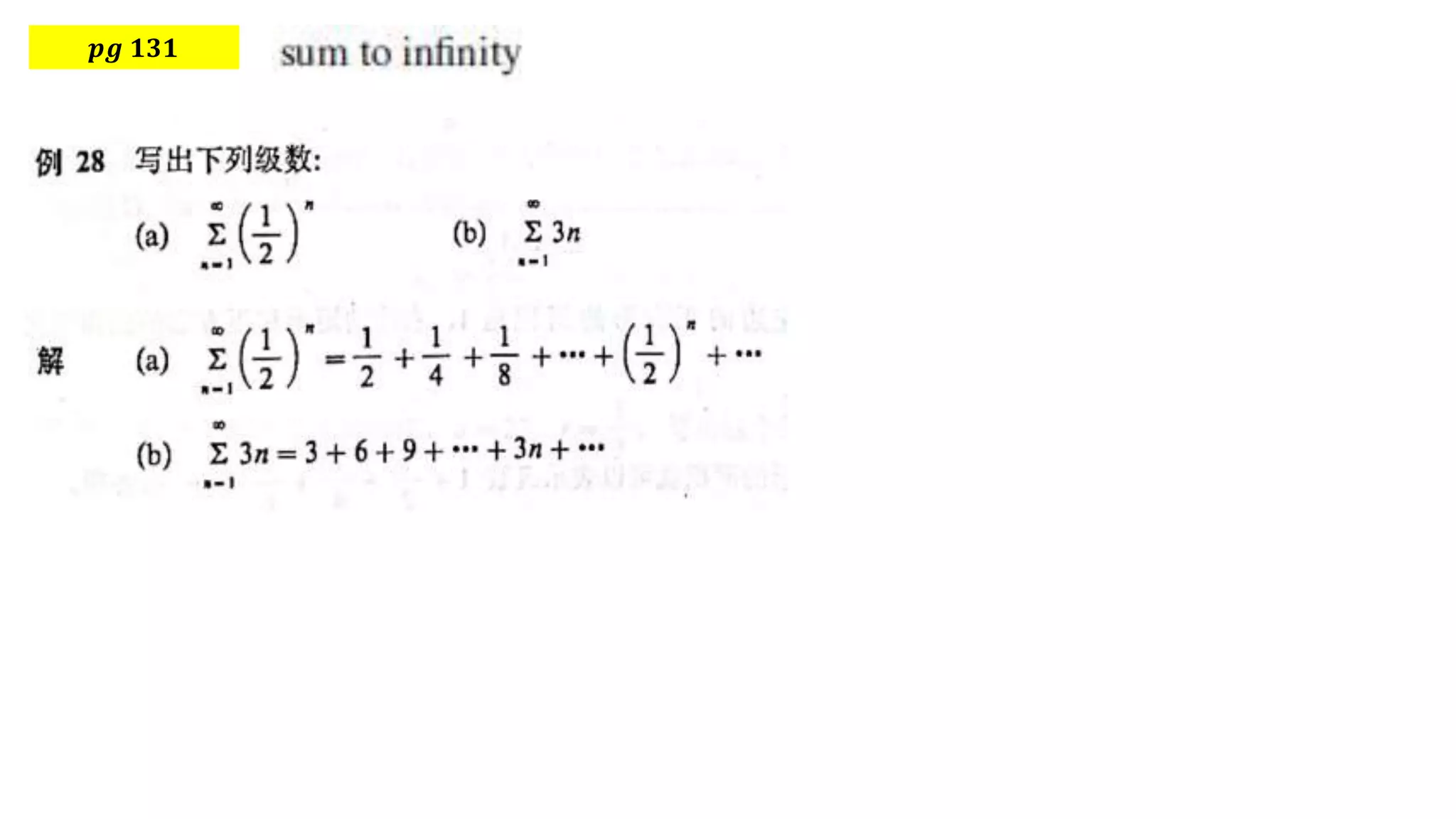
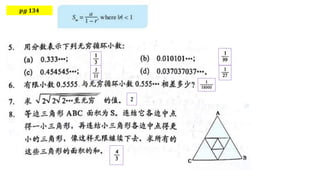
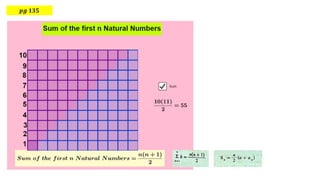
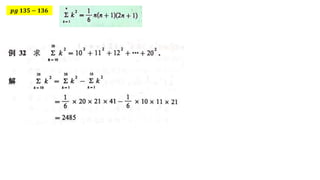
The document provides mathematical formulations and approaches to problem-solving, including a discussion on recurring numbers and the area of an equilateral triangle. It introduces concepts of infinite series and connections between geometrical elements. Additionally, the document includes algebraic expressions related to summing series and polynomial functions.

1. 𝒑𝒈 𝟏𝟑𝟏

2. 𝒑𝒈 𝟏𝟑𝟐

3. 𝒑𝒈 𝟏𝟑𝟑

4. 𝒑𝒈 𝟏𝟑𝟒

5. 𝒑𝒈 𝟏𝟑𝟒
A dot over a number represents a recurring number.

7. 𝒑𝒈 𝟏𝟑𝟒

8. 𝒑𝒈 𝟏𝟑𝟒
2 = 2
1
2
2 2 = 2 × 2
1
2
1
2
= 2
1
2 × 2
1
4
2 2 2 = 2 2 × 2
1
2
1
2
1
2
= 2
1
2 × 2
1
4 × 2
1
8 = 2
1
2 +
1
4 +
1
8
2 2 2 . . . = 2
1
2 +
1
4 +
1
8 + ...
= 2
1
2 1−
1
2
= 2

9. 𝒑𝒈 𝟏𝟑𝟒
The area of equilateral triangle ABC is S.
Connect the midpoints of its sides
to the midpoints of the triangles.
Get a small triangle, then connect the small triangles,
sum of infinite triangles = ?
𝑎𝑠𝑠𝑢𝑚𝑒 𝐴𝐴𝐵𝐶 = 𝑆 = 1
𝐴𝑚𝑖𝑑𝑝𝑜𝑖𝑛𝑡 ∆ =
𝑆
4
=
1
4
𝑟 =
1
4
𝑆∞ =
1
1 −
1
4
=
4
3

10. 𝒑𝒈 𝟏𝟑𝟓

11. 𝒑𝒈 𝟏𝟑𝟓 − 𝟏𝟑𝟔

12. 𝒑𝒈 𝟏𝟑𝟕

13. 𝒑𝒈 𝟏𝟑𝟕

14. 𝒑𝒈 𝟏𝟑𝟕

15. 𝒑𝒈 𝟏𝟑𝟕

16. 𝒑𝒈 𝟏𝟑𝟕
= 4𝑛3
+ 4𝑛 − 6𝑛2
− 𝟏
= 4
1
4
𝑛2 𝑛 + 1 2 + 4
𝑛 𝑛 + 1
2
− 6
1
6
𝑛 𝑛 + 1 2𝑛 + 1 − 𝒏
= 𝑛2
𝑛 + 1 2
+ 2𝑛 𝑛 + 1 − 𝑛 𝑛 + 1 2𝑛 + 1 − 𝑛
= 𝑛2
(𝑛2
+ 2𝑛 + 1) + 2𝑛2
+ 2𝑛 − 𝑛(2𝑛2
+ 3𝑛 + 1 − 𝑛
= 𝑛4 + 2𝑛3 + 𝑛2 + 2𝑛2 + 2𝑛 − 2𝑛3 − 3𝑛2 − 𝑛 − 𝑛
= 𝑛4
= 4
𝑘=1
𝑛
𝑘3
+ 4
𝑘=1
𝑛
𝑘 − 6
𝑘=1
𝑛
𝑘2
− 𝜮 𝟏

17. 𝒑𝒈 𝟏𝟑𝟖