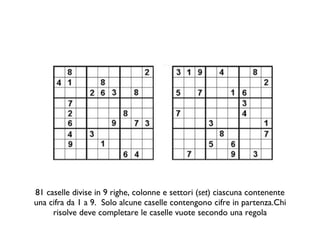
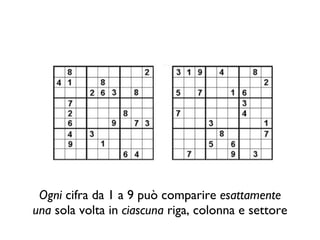
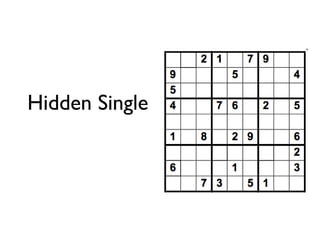
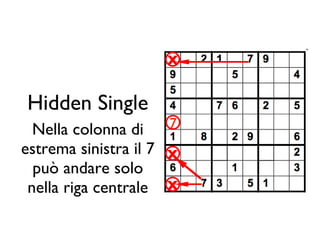
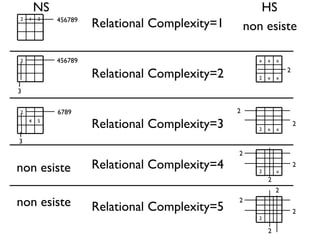
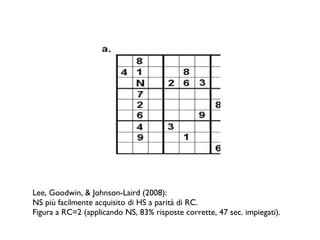
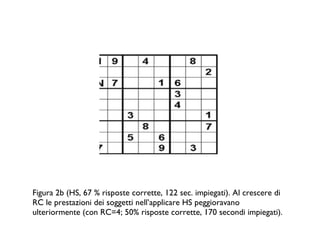
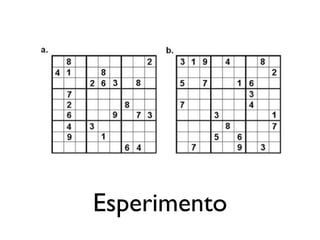
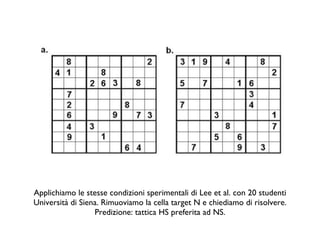
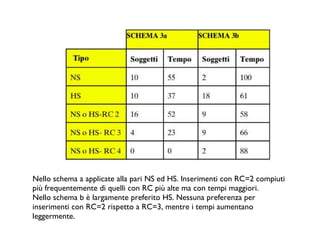
Il documento analizza come il Sudoku sfidi le capacità deduttive, confrontando i modelli mentali e la cognizione distribuita. Si evidenziano due strategie principali, il 'hidden single' e il 'naked single', e come la complessità relazionale influenzi l'efficacia di queste tattiche. Le conclusioni indicano che le rappresentazioni esterne aiutano ad applicare tattiche di ragionamento, confermando l'importanza del contesto nella risoluzione di problemi complessi come il Sudoku.

1. Il sudoku tra teoria dei Modelli Mentali e Cognizione distribuita Marco Carnesecchi & Antonio Rizzo Università degli studi di Siena

2. Che cos’è il Sudoku ?

3. 81 caselle divise in 9 righe, colonne e settori ( set ) ciascuna contenente una cifra da 1 a 9. Solo alcune caselle contengono cifre in partenza.Chi risolve deve completare le caselle vuote secondo una regola

4. Ogni cifra da 1 a 9 può comparire esattamente una sola volta in ciascuna riga, colonna e settore

5. Dalla vita quotidiana allo studio del ragionamento deduttivo Il sudoku è un task che mette alla prova le stesse capacità dei sillogismi (Bara, Bucciarelli, & Johnson-Laird, 1995; Rizzo & Palmonari, 2005) o del compito di selezione di Wason (Wason 1966). Oltre a mostrare come le persone siano capaci e si divertano nel compiere deduzioni (logica del primo ordine a tre quantificatori) anche senza aver mai studiato logica, il sudoku ha due caratteristiche peculiari rispetto ai tasks di laboratorio: Le premesse non sono fornite dallo sperimentatore ma ricavabili dallo schema. Le deduzioni non sono self-standing ma multi-step, ogni conclusione fa da premessa per inferenze successive.

6. Hidden Single vs Naked Single Protocolli verbali ricavati da soggetti di varia esperienza su un intero schema con thinking aloud suggeriscono due tattiche base più altre avanzate che tratteremo altrove. (Carnesecchi&Rizzo in preparazione) HS: Focus sulle cifre. “ Se una cifra tra i candidati possibili per una cella può comparire solo in quella cella all’interno della riga, della colonna o del settore del quale la cella fa parte allora la cella conterrà quella cifra” NS: Focus sulle celle. “ Se una cella può contenere una sola cifra allora essa conterrà quella cifra”

7. Hidden Single

8. Hidden Single Nella colonna di estrema sinistra il 7 può andare solo nella riga centrale X X X 7

9. Naked Single

10. Naked Single L’8 in alto a destra è l’unica cifra possibile 8

11. Relational Complexity La difficoltà di elaborazione di ciascun compito corrisponde al numero di variabili interagenti che devono essere rappresentate in parallelo per eseguire la più complessa elaborazione che il compito richiede utilizzando la strategia inferenziale più economica (Halford et al. 1998) Nel ragionamento proposizionale: maggiore difficoltà in test che richiedono la rappresentazione di relazioni a più argomenti (Goodwin & Johnson-Laird 2005) Es. A>B più semplice di A>B>C “ A>B più di quanto C>D” più difficile da comprendere rispetto a “A>B più di quanto A>D”

12. Relational Complexity & Sudoku HS: RC uguale al numero di occorrenze di una cifra che permettono di individuarla come unico candidato possibile più il set di appartenenza NS: RC uguale al numero di set nei quali sono collocate le cifre da escludere per compiere l’inferenza

13. Relational Complexity=4 Relational Complexity=5 Relational Complexity=3 Relational Complexity=2 Relational Complexity=1 2 2 2 2 2 2 2 2 456789 456789 1 3 6789 1 3 2 2 NS HS non esiste non esiste non esiste 2 1 3 2 2 4 5 x x x 2 x x 2 x x 2 x 2

14. Lee, Goodwin, & Johnson-Laird (2008): NS più facilmente acquisito di HS a parità di RC. Figura a RC=2 (applicando NS, 83% risposte corrette, 47 sec. impiegati).

15. Figura 2b (HS, 67 % risposte corrette, 122 sec. impiegati). Al crescere di RC le prestazioni dei soggetti nell’applicare HS peggioravano ulteriormente (con RC=4; 50% risposte corrette, 170 secondi impiegati).

16. Ipotesi Gli schemi a e b sono ecologiamente diversi dal sudoku quotidiano. Indicare una cella target facilita l’applicazione di NS a discapito di HS perché NS richiede il focus sulle celle vuote mentre non cambia niente per HS dato che HS richiede il focus sulle cifre. Nei sudoku HS richiede di esplicitare al massimo 4 occorrenze della stessa cifra, identica a quella da trovare.

17. Ipotesi NS richiede di esplicitare sempre 8 cifre per escluderle . TMM: se le premesse da considerare per costruire un modello sono esplicite (HS) la deduzione dovrebbe essere più facile (Johnson-Laird & Byrne 2002) Rimuovendo la cella target N dagli schemi quanto conta RC?

18. Esperimento

19. Applichiamo le stesse condizioni sperimentali di Lee et al. con 20 studenti Università di Siena. Rimuoviamo la cella target N e chiediamo di risolvere. Predizione: tattica HS preferita ad NS.

20. Risultati

21. Nello schema a applicate alla pari NS ed HS. Inserimenti con RC=2 compiuti più frequentemente di quelli con RC più alte ma con tempi maggiori. Nello schema b è largamente preferito HS. Nessuna preferenza per inserimenti con RC=2 rispetto a RC=3, mentre i tempi aumentano leggermente.

22. Conclusioni Due fenomeni che si verificano mentre le persone risolvono il sudoku ci suggeriscono una revisione delle principali teorie di ragionamento deduttivo: Chi risolve è in grado di imparare le tattiche base, spiegarle esplicitamente senza che lo sperimentatore le abbia prima suggerite e passare indistintamente da una all’altra. Ciò smentisce l’assunto delle teorie basate su regole di inferenza formali secondo cui le persone ragionano secondo una singola e fissa strategia deterministica. Quando HS & NS falliscono chi risolve è in grado di capire che è necessario uno shift a strategie che abbiano come premessa le cifre possibili e non le cifre definite. Attraverso il sudoku la TMM si confronta con problemi multi-step, ma non è in grado di spiegare l’acquisizione e la preferenza una tattica. Perciò Lee et al. propongono la RC come fattore che orienta la preferenza di una strategia a favore di un’altra.

23. Conclusioni Restituendo al sudoku validità ecologica (analizzando un intero schema) emerge invece invece il ruolo chiave delle rappresentazioni esterne nell’apprendere ed applicare le tattiche. Le rappresentazioni esterne contribuiscono a costruire i Modelli Mentali favorendo la scelta di una premessa ai danni di un’altra (Rizzo & Palmonari 2005). Nel sudoku esse creano affordances per l’uso di HS a discapito di NS. NS è appresa prima perché il focus è su una singola cella invece di un intero set. NS richiede un’operazione più semplice una volta individuata la giusta cella, ma HS prevale perché le premesse da considerare sono in numero inferiore, rappresentate più esplicitamente ed isomorfe alla conclusione.

24. Conclusioni Il principio di verità della TMM si applica al sudoku: ogni MM rappresenta ciò che conferma le premesse, ma per definizione non ciò che le confuta. Nel sudoku: per applicare HS non serve considerare tutti candidati possibili per una cella (ovvero esplicitare il MM). Per applicare NS ogni candidato possibile va considerato, ciò è più semplice quando le rappresentazioni esterne (la configurazione dello schema) lo suggeriscono. Le rappresentazioni esterne aiutano ad acquisire tattiche di ragionamento più complesse.