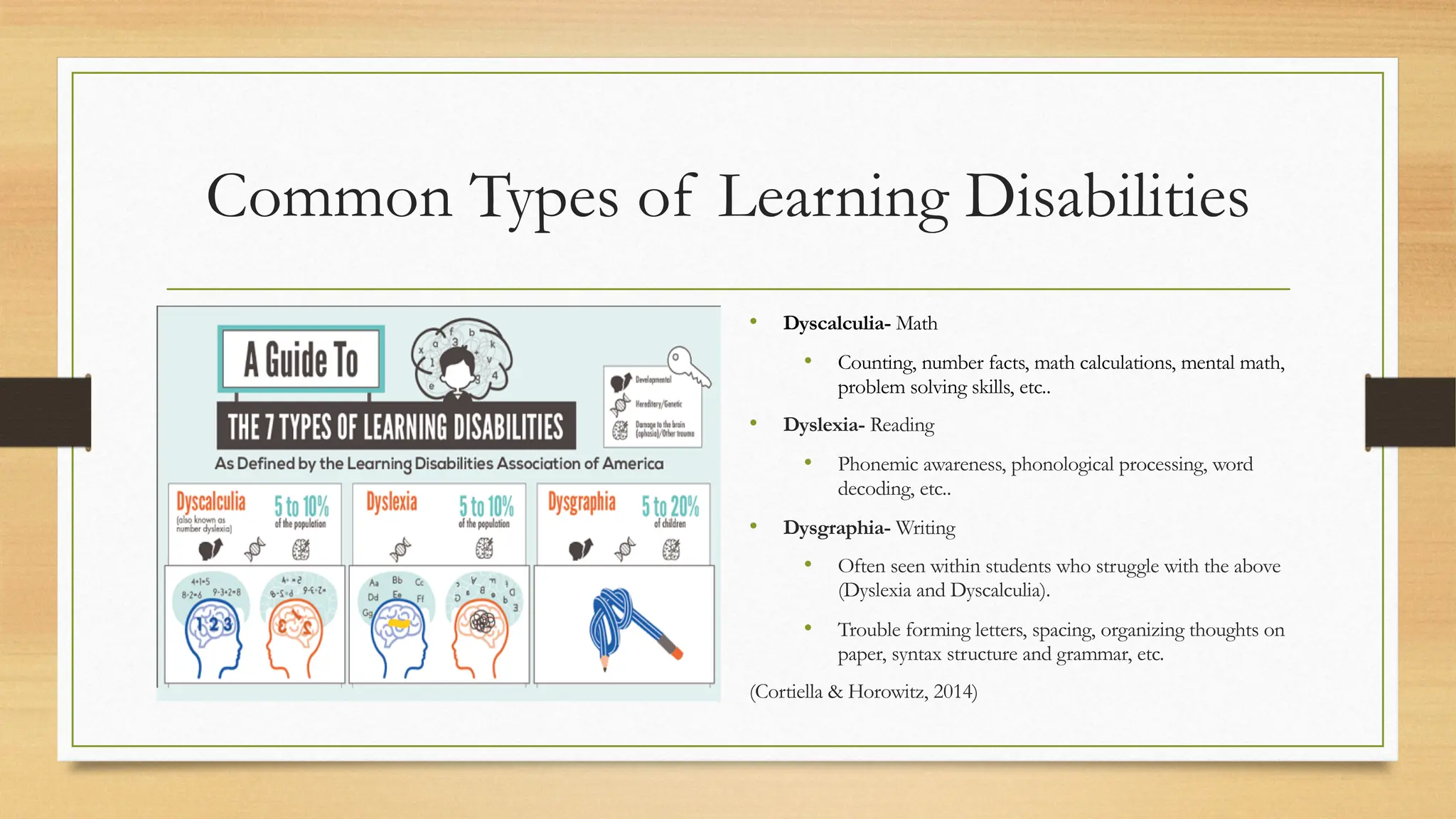
The document discusses learning disabilities (LD) and their impact on students' ability to perform in mathematics, highlighting common types of LD such as dyscalculia, dyslexia, and dysgraphia. It identifies various factors that contribute to math difficulties in students with LD, including cognitive deficits, instructional methods, and learner characteristics. Additionally, it offers strategies for teachers to better support these students through explicit instruction, mathematical language, and problem-solving approaches.