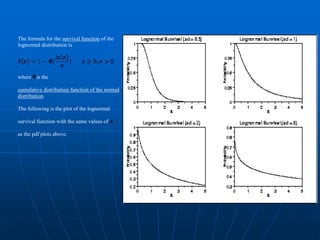
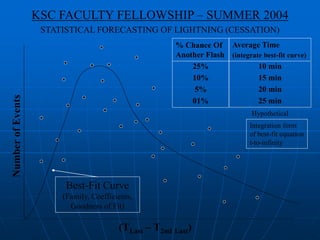
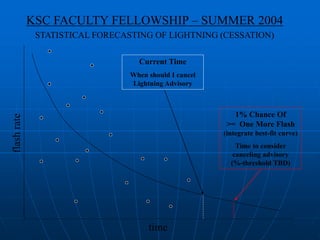
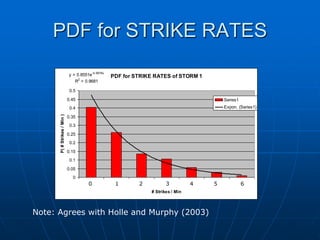
The document describes a project to develop statistical models for forecasting lightning cessation in thunderstorms. It aims to analyze lightning flash rates over time in decaying storms to estimate the probability of additional flashes and determine optimal times to cancel lightning advisories. The project involved analyzing 58 storms and developing climatological distributions and curve fits of flash rates. Preliminary results provided probability thresholds and wait times that could guide decisions on when to end advisories. Further work was proposed to refine the models and develop software to apply the statistical techniques in operations.

1. KSC’s 2004 NFFP:
Statistical Forecasting of Lightning
Cessation
Jim E. Glover
Oral Roberts University
William P. Roeder, 45 WS/SYR
Francis J. Merceret, YA-D
William H. Bauman III, AMU
Dave A. Short, AMU

2. Statistical Forecasting of Lightning
Cessation
Project Team
Fellow:
• Jim E. Glover
• Oral Roberts University
NASA Colleagues
• William P. Roeder 45 WS/SYR/ROCC
• Francis J. Merceret KSC/YA-D/ROCC
• William H. Bauman, III ENSCO/AMU/ROCC
• Dave A. Short ENSCO/AMU/ROCC
Project Scope
Problem/Objective:
• Apply statistical curve fitting to the slowing lightning
flash rate in decaying thunderstorms to estimate the
probability of occurrence of one or more flashes and
simulate decisions to cancel advisories
Deliverables
• Project report reflecting a climatology and a time
series for strikes using best fit curves to observed
distribution times vs. number of strikes
• KSC and 45 WS briefings on results and algorithms
Outcomes to KSC
Programs
• CGLSS, LDAR
Short-term
• Reduction of time-frame required for leaving lightning
advisories in effect
• Development of a well-defined climatology on the
probability distribution of times between the next-to-last
and last flashes, based upon continuous surveillance
Long-Term
• Transfer of technology to other areas (e.g., space shuttle
flight support)
• Development of an analytical reliability analysis tool
or technique which may be useful in other areas
Outcomes to Faculty
Overall
• A critical application of a statistical and scientific
approach to a real-life problem which affects society
Teaching
• Incorporation of NASA’s philosophy into the training of
students for critical scientific work
• Analysis of an actual application which may be of some
inspiration to students for future work
Research
• Presentation of a paper or talk at a minimum of two
forums or conferences during the ensuing year
• Development of a new paradigm that may be useful
throughout the aerospace engineering industry

3. Operational Challenge
45 WS needs to end lightning advisories sooner,
while maintaining safety
 Very tough technical challenge
 Little objective guidance available
- So, for safety, 45 WS has to be
conservative in ending lightning advisories
 Costly to CCAFS/KSC ground processing
operations
 One of 45 WS’s “strategic goals” for 2004

4.  Long-Term Vision:
Development of software that
will automatically analyze
lightning flash-rates for local
storms in real-time and flag
the storms that are decaying,
flag the storms whose
advisories should be
considered for canceling

5. or indicate the elapsed time
expected until the probability
of at least one more flash
falls below some desired
threshold
-- Given the technical challenge,
this project is considered
high-risk/high-return.

6. Methodology
 Restricted analysis to CGLSS data
(only cloud-to-ground lightning
considered)
 58 convective season storms analyzed
 59th “composite” storm created, consisting
of the mean of all 58 storm strike-rates
over each unit time interval

7. Sample Years
Year Number of Storms
1999 12
2000 13
2001 14
2002 7
2003 12

8. CG Strike Flash Rate - 30 Jul 03
0
1
2
3
4
5
6
7
8
9
0:02
0:09
0:16
0:23
0:30
0:37
0:44
0:51
0:58
1:05
1:12
1:19
1:26
1:33
1:40
1:47
1:54
2:01
2:08
2:15
2:22
2:29
2:36
2:43
Time(Z)
#CGStrikes
CG Strikes

9. 1. Climatological distribution of
times between last flash and next
to last flash
2. Curve fitting of slowing flash
rates in the decaying phase of a
thunderstorm
Two Approaches

10.  Times between last two flashes
 Generates empirical chart
 Provides probability that most recent flash
is last one, given time history
 Also gives time interval corresponding to a
specified probability of another flash
 Forecaster can use to determine when to
cancel Phase II
Climatological Distribution Method

11. KSC FACULTY FELLOWSHIP – SUMMER 2004
STATISTICAL FORECASTING OF LIGHTNING (CESSATION)
(TLast – T2nd Last)
NumberofEvents
Best-Fit Curve
(Family, Coefficients,
Goodness of Fit)
% Chance Of
Another Flash
25%
10%
5%
01%
Average Time
(integrate best-fit curve)
10 min
15 min
20 min
25 min
Hypothetical
Integration form
of best-fit equation
t-to-infinity

12. PDF(DELTA-t)
PDF of DELTA-t y = -0.0469Ln(x) + 0.1493
R2
= 0.7509
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0 5 10 15 20 25
DELTA-t
P(DELTA-t)
Series1
Log. (Series1)

13. Z-Score of Ln(Displacement)
y = 0.7604x - 1.3254
R
2
= 0.997
-1.5
-1
-0.5
0
0.5
1
1.5
0 1 2 3 4
Ln( Displacment )
Z-Score
Z-Score
Linear (Z-Score)

14.  Slowing flash rates in decaying phase
 Derive probability that there will be
at least one more flash in a specified
time
 Derive probability that most recent
flash is the last one
Curve-Fitting Method

15. KSC FACULTY FELLOWSHIP – SUMMER 2004
STATISTICAL FORECASTING OF LIGHTNING (CESSATION)
time
flashrate
1% Chance Of
>= One More Flash
(integrate best-fit curve)
Time to consider
canceling advisory
(%-threshold TBD)
Current Time
When should I cancel
Lightning Advisory

16. Reliability of Strike Rates
Survivability/Reliability of Strike Rates
y = -0.3085Ln(x) + 1.7599
R2
= 0.8642
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 50 100 150 200 250
Time (Minutes)
Reliability
y
Log. (y)

17. Survival/Reliability Curve for Composite Storm
y = 5E-14x6
- 2E-11x5
- 1E-09x4
+ 1E-06x3
- 0.0002x2
+ 0.0004x + 0.9909
R2
= 1
0
0.2
0.4
0.6
0.8
1
1.2
1 14 27 40 53 66 79 92 105 118 131 144 157 170 183 196 209 222
# Minutes
P(#Minutes)
Series1
Poly. (Series1)

18. PDF for STRIKE RATES
PDF for STRIKE RATES of STORM 1y = 0.8551e-0.5876x
R2
= 0.9681
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
1 2 3 4 5 6 7
# Strikes / Min
P(#Strikes/Min)
Series1
Expon. (Series1)
0 1 2 3 4 5 6
Note: Agrees with Holle and Murphy (2003)

19. ==============================================================================
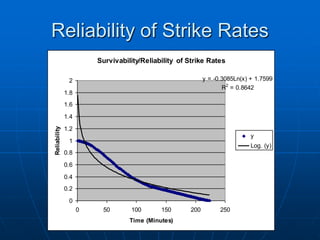
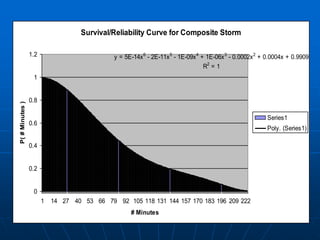
MATRIX OF RELIABILITIES WITH CORRESPONDING TIMES AND MEAN TIMES TO FAILURE
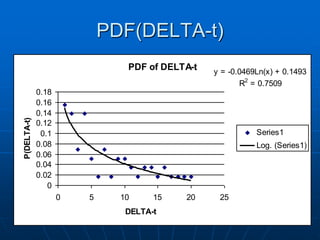
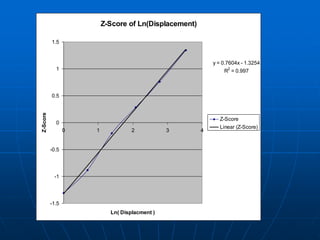
R(t) = 1 - F(t) = P( T > t ) for the random variable T ,
where T is the time to failure (or storm cessation)
( NOTE: TMIN <====> Total # Elapsed Minutes per Event )
( Cancel after t minutes to be [100-R(t)] % certain of no more strikes.)
[*] <====> The Composite Storm
==============================================================================
------- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
R(t) --> 50 % 45 % 40 % 30 % 20 % 15 % 10 % 5 % 3 % 1 % TMIN
------- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
EVENT # TIME t TO FAILURE for each R(t)
------- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
1 ). 40 44 48 55 64 76 83 88 89 93 --> 98
2 ). 52 56 61 97 127 145 199 237 246 249 --> 260
3 ). 104 107 110 114 120 124 130 148 155 164 --> 208
4 ). 35 38 40 44 48 51 59 61 63 65 --> 65
. . . . .
. . . . .
. . . . .
57 ). 112 119 122 130 140 146 246 256 259 270 --> 303
58 ). 40 44 48 55 64 76 83 88 89 93 --> 98
59 ).[*] 75 82 89 108 139 160 179 199 205 215 --> 219
------- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
MEAN t --> 65 68 71 77 84 90 99 109 113 125 --> 141
------- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
StdDev --> 43 44 44 46 47 47 54 55 55 77
------- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
Mean Duration of Storms = mu = 139 Minutes
Mean Total Number of Strikes per Storm = 339 Strikes

20. SUMMARY
 58 local thunderstorms analyzed,
leading to a composite storm
 Climatological distributions of Delta-t
developed
-- Available for immediate
operational use
 Probability thresholds vs. wait-time
determined

21. SUMMARY (continued)
Preliminary proof-of-concept for
curve-fitting of flash rates in
decaying thunderstorms to
predict probabilities and timing
of last flash
Further developmental work justified

22. FUTURE PLANS
 Test techniques on independent
cases
 Increase sample size
 Filter better for individual
thunderstorms and their
decay phase

23. Future Plans (continued)
 Include complex multi-cellular
organized storms
 Expand study to utilize LDAR
(all types of lightning, including
lightning aloft, not just
cloud-to-ground lightning as
detected by CGLSS)
 Hope for Phase II and Phase III in
summers of 2006 and 2007, resp.

24. Software Developed
======================== PROGRAM A-STAR ========================
A-STAR READS A SEQUENCE OF NUMBERS OF STRIKES AT A SEQUENCE OF
TIMES, t, IN UNIT INCREMENTS OF MINUTES AND DETERMINES STRIKE RATES
AND TIME DISPLACEMENTS BETWEEN THE (2ND-TO-LAST AND LAST) STRIKES
AND BETWEEN THE (3RD-TO-LAST AND 2ND-TO-LAST) STRIKES, TO GENERATE
A CLIMATOLOGY FOR TIME DISPLACEMENTS BETWEEEN STRIKES, AND TO
DETERMINE OPTIMAL TIMES FOR CANCELLING ADVISORIES, BASED UPON
EMPIRICALLY COMPUTED RELIABILITIES DERIVED FROM STORM SIGNATURES.
THE ROUTINE GENERATES A CUMULATIVE DISTRIBUTION F(t) AS A FUNCTION
OF TIME t AND A CORRESPONDING RELIABILITY FUNCTION R(t) FOR THE
RANDOM VARIABLE T, WHERE T IS THE EXPECTED OR MEAN TIME TO FAILURE
(E.G., CESSATION OF LIGHTNING STRIKES) IN A MEASURED STORM.
THE RELIABILITY AT TIME t IS GIVEN BY: R(t) = 1 - F(t) = P( T > t ).
THE ANALYST IS QUERIED FOR A DESIRED MAXIMUM PROBABILITY (%)
FOR THE EXPECTED OCCURRENCE OF ONE OR MORE LIGHTNING STRIKES AND THE
ROUTINE DETERMINES THE TIME t CORRESPONDING TO THE RELIABILITY R(t).
A SUMMARY FILE IS GENERATED INTO A-STAR.OT0, CONSISTING OF:
STORM #, DATE OF STORM, DURATION TIME PER STORM, AND CUMULATIVE
NUMBER OF STRIKES PER STORM.
==================================================================

25. Software Developed (continued)
======================== PROGRAM B-STAR ========================
B-STAR READS A SEQUENCE < t > OF VALUES OF SOME RANDOM VARIABLE
T (e.g., LIGHTNING DISPLACEMENTS IN MINUTES BETWEEN 2ND-TO-LAST
AND LAST STRIKES OR BETWEEN 3RD-TO-LAST AND 2ND-TO-LAST STRIKES,
GENERATING A CLIMATOLOGY FOR TIME DISPLACEMENTS BETWEEEN STRIKES
AND DETERMINING OPTIMAL TIMES FOR CANCELLING ADVISORIES, BASED UPON
EMPIRICALLY COMPUTED RELIABILITIES DERIVED FROM STORM SIGNATURES.)
THE ROUTINE GENERATES FREQUENCY/CUMULATIVE FREQUENCY DISTRIBUTIONS,
BASED UPON TACIT SORTING, BINNING, AND NORMALIZATION. A RELIABILITY
DISTRIBUTION R(t) IS GENERATED FOR THE RANDOM VARIABLE T, WHERE t
IS THE EXPECTED OR MEAN DISPLACEMENT TIME TO FAILURE ( e.g., THE
OCCURRENCE OF AT LEAST ONE MORE STRIKE TIME DISPLACEMENT HAVING
SIZE EXCEEDING g(T) ) FOR SOME FUNCTION g. MOREOVER, THE ANALYST
IS PROMPTED FOR A DESIRED MAXIMUM PROBABILITY (%) FOR THE EXPECTED
OCCURRENCE OF AT MOST ONE MORE VALUE OF g(T) FOR WHICH T EXCEEDS
t AND THE ROUTINE DETERMINES THE VALUE t CORRESPONDING TO THE
RELIABILITY R(t). (NOTE, E.G., THAT IS IS NATURALLY EXPECTED THAT
DECREASING NUMBERS OF STORMS WILL HAVE INCREASING NUMBERS OF
TIME DISPLACEMENTS BETWEEN SUCCESSIVE LIGHTNING STRIKES.)
==================================================================

26. Software Developed (continued)
======================== PROGRAM C-STAR ========================
C-STAR READS A SEQUENCE OF BLOCKS OF EVENTS, EACH CONSISTING OF
A SEQUENCE OF NUMBERS OF LIGHTNING STRIKES AT A SEQUENCE OF TIMES,
t, IN UNIT INCREMENTS OF MINUTES AND DETERMINES STRIKE RATES AND
TIME DISPLACEMENTS BETWEEN THE (2ND-TO-LAST AND LAST) STRIKES
OR BETWEEN THE (3RD-TO-LAST AND 2ND-TO-LAST) STRIKES, TO GENERATE
A CLIMATOLOGY FOR TIME DISPLACEMENTS BETWEEEN STRIKES, AND TO
DETERMINE OPTIMAL TIMES FOR CANCELLING ADVISORIES, BASED UPON
EMPIRICALLY COMPUTED RELIABILITIES DERIVED FROM STORM SIGNATURES.
A RELIABILITY DISTRIBUTION IS ALSO GENERATED FOR THE RANDOM
VARIABLE T, WHERE T IS THE EXPECTED OR MEAN TIME TO FAILURE
(CESSATION OF LIGHTNING STRIKES) IN EACH MEASURED STORM. THIS
PROCESS IS CYCLICALLY REPEATED FOR EACH STORM IN THE SEQUENCE.
THE ROUTINE THEN GENERATES A MATRIX OF TIMES t CORREESPONDING
TO A DESIRED SEQUENCE OF RELIABILITIES, R(t), AS WELL AS THE
AVERAGE VALUE OF t ASSOCIATED WITH EACH VALUE OF R(t), WHERE
R(t) = 1 - F(t) = P( T > t) AND F(t) IS THE CUMULATIVE
DISTIBUTION OF T. R(t), THE RELIABILITY OF T AT TIME t, IS
THE PROBABILITY (%) OF THE EXPECTED OCCURRENCE OF ONE OR MORE
LIGHTNING STRIKES AFTER TIME t.
==================================================================

27. Software Developed (continued)
======================== PROGRAM D-STAR ========================
D-STAR READS A SEQUENCE OF PMAX STORM EVENTS CONSISTING OF
Q0 VARYING LIGHTNING STRIKE RATES AS A FUNCTION OF TIME t IN UNIT
INCREMENTS OF MINUTES AND DETERMINES A COMPOSITE STORM, CONSISTING
OF V0 COMPUTED MEAN STRIKE RATES AT EACH TIME t , WHERE THE
TIME DURATION OF STORMS VARIES. THE ROUTINE THEN DETERMINES
TIME DISPLACEMENTS BETWEEN THE (2ND-TO-LAST AND LAST) STRIKES
AND BETWEEN THE (3RD-TO-LAST AND 2ND-TO-LAST) STRIKES,GENERATING
TIME DISPLACEMENTS BETWEEEN STRIKES FOR THE COMPOSITE STORM AND
DETERMINING OPTIMAL TIMES FOR CANCELLING ADVISORIES, BASED UPON
EMPIRICALLY COMPUTED RELIABILITIES DERIVED FROM THE STORM SIGNATURE.
THE ROUTINE GENERATES A CUMULATIVE DISTRIBUTION F(t) AS A FUNCTION
OF TIME t AND A CORRESPONDING RELIABILITY FUNCTION R(t) FOR THE
RANDOM VARIABLE T, WHERE T IS THE EXPECTED OR MEAN TIME TO FAILURE
(E.G., CESSATION OF LIGHTNING STRIKES) IN A MEASURED STORM.
THE RELIABILITY AT TIME t IS GIVEN BY: R(t) = 1 - F(t) = P( T > t ).
THE ANALYST IS QUERIED FOR A DESIRED MAXIMUM PROBABILITY (%)
FOR THE EXPECTED OCCURRENCE OF ONE OR MORE LIGHTNING STRIKES AND THE
ROUTINE DETERMINES THE TIME t CORRESPONDING TO THE RELIABILITY R(t).
THE ANALYST MAY ENTER A DESIRED MAXIMUM VALUE FOR THE INTEGER-VALUED
DURATION TIMES IN MINUTES FOR EACH STORM TO BE SELECTED FROM
D-STAR.INP AND ANALYZED. THE MAXIMUM DIMENSIONS OF P(N,M) <===>
P(10,400), WHERE N IS THE NUMBER OF STORMS AND M IS THE NUMBER OF
MINUTES OF DURATION. A FILE OF THE STORM WITH MEAN VALUES OF
NUMBER OF STRIKES AT TIME t IS GENERATED INTO D-STAR.OT8.
D-STAR IS A VARIANT OF A-STAR.
==================================================================

28. Software Developed (continued)
======================== PROGRAM E-STAR ========================
E-STAR READS A SEQUENCE OF PMAX STORM EVENTS CONSISTING OF
Q0 VARYING LIGHTNING STRIKE RATES AS A FUNCTION OF TIME t IN UNIT
INCREMENTS OF MINUTES AND DETERMINES A COMPOSITE STORM, CONSISTING
OF V0 COMPUTED MEAN STRIKE RATES AT EACH TIME t , WHERE THE
TIME DURATION OF STORMS VARIES. THE ROUTINE THEN DETERMINES
TIME DISPLACEMENTS BETWEEN THE (2ND-TO-LAST AND LAST) STRIKES
AND BETWEEN THE (3RD-TO-LAST AND 2ND-TO-LAST) STRIKES,GENERATING
TIME DISPLACEMENTS BETWEEEN STRIKES FOR THE COMPOSITE STORM AND
DETERMINING OPTIMAL TIMES FOR CANCELLING ADVISORIES, BASED UPON
EMPIRICALLY COMPUTED RELIABILITIES DERIVED FROM THE STORM SIGNATURE.
THE ROUTINE GENERATES A CUMULATIVE DISTRIBUTION F(t) AS A FUNCTION
OF TIME t AND A CORRESPONDING RELIABILITY FUNCTION R(t) FOR THE
RANDOM VARIABLE T, WHERE T IS THE EXPECTED OR MEAN TIME TO FAILURE
(E.G., CESSATION OF LIGHTNING STRIKES) IN A MEASURED STORM.
THE RELIABILITY AT TIME t IS GIVEN BY: R(t) = 1 - F(t) = P( T > t ).
THE ANALYST IS QUERIED FOR A DESIRED MAXIMUM PROBABILITY (%)
FOR THE EXPECTED OCCURRENCE OF ONE OR MORE LIGHTNING STRIKES AND THE
ROUTINE DETERMINES THE TIME t CORRESPONDING TO THE RELIABILITY R(t).
THE DETERMINES THE MAXIMUM STORM DURATION, DMAX, AND UTILIZES THIS
DURATION TIME IN MINUTES FOR EACH STORM TO BE SELECTED FROM
E-STAR.INP AND ANALYZED. THE MAXIMUM DIMENSIONS OF P(N,M) <===>
P(40,400), WHERE N IS THE NUMBER OF STORMS AND M IS THE NUMBER OF
MINUTES OF DURATION. A CUMULATIVE FILE OF STORMS WITH MEAN VALUES
OF NUMBER OF STRIKES AT TIME t IS GENERATED INTO E-STAR.OT9.
E-STAR IS A VARIANT OF D-STAR.
==================================================================

29. Software Developed (continued)
======================== PROGRAM F-STAR ========================
F-STAR READS A SEQUENCE OF PMAX STORM EVENTS CONSISTING OF Q0
VARYING LIGHTNING STRIKE RATES AS A FUNCTION OF TIME t IN UNIT
INCREMENTS OF MINUTES AND FILTERS THOSE STORMS FROM THE SEQUENCE
FOR WHICH TM LIES IN THE DESIRED INTERVAL [ T1,T2 ] AND
CS LIES IN THE DESIRED INTERVAL [ CS1,CS2 ] , WHERE TM
IS THE TOTAL DURATION OF EACH STORM (IN MINUTES) AND CS
IS THE CUMULATIVE NUMBER OF STRIKES OF EACH STORM. FILTERED
STORMS ARE PRINTED IN F-STAR.OT2 WITH HEADERS FOR FURTHER
ANALYSIS.
==================================================================

30. Software Developed (continued)
======================== PROGRAM G-STAR ========================
G-STAR READS A SINGLE STORM EVENT CONSISTING OF Q0 VARYING
LIGHTNING STRIKE RATES AS A FUNCTION OF TIME t IN UNIT INCREMENTS
OF MINUTES AND PRINTS THE MEASUREMENTS AS EITHER A-STAR.INP OR
B-STAR.INP.
==================================================================

31. Modeling Failure Times
The lognormal distribution is used extensively in
reliability applications to model failure times. The
lognormal and Weibull distributions are probably the
most commonly used distributions in reliability
applications.

32. Lognormal Distribution
Probability
Density
Function
A variable X is lognormally distributed if Y = LN(X) is
normally distributed with "LN" denoting the natural logarithm.
The general formula for the probability density function of the
lognormal distribution is
where is the shape parameter, is the location parameter and
m is the scale parameter. The case where = 0 and m = 1 is
called the standard lognormal distribution. The case where
equals zero is called the 2-parameter lognormal distribution.
The equation for the standard lognormal distribution is
Since the general form of probability functions can be
expressed in terms of the standard distribution, all subsequent
formulas in this section are given for the standard form of the
function.

33. The formula for the survival function of the
lognormal distribution is
where is the
cumulative distribution function of the normal
distribution.
The following is the plot of the lognormal
survival function with the same values of
as the pdf plots above.

34. Standard Lognormal Statistics
The formulas below are with the location parameter
equal to zero and the scale parameter equal to one.
Mean
Median Scale parameter m (= 1 if scale
parameter not specified).
Mode
Range Zero to positive infinity
Standard
Deviation
Skewness
Kurtosis
Coefficient of
Variation

35. Questions ?