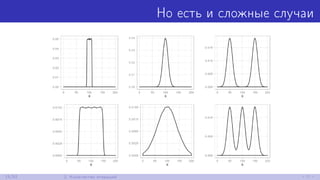
Документ исследует сложности микробенчмаркинга на примере C#, обсуждая важность и применение бенчмарков для анализа производительности и сравнения алгоритмов. В ходе презентации рассматриваются различные аспекты, такие как количество итераций, работа с памятью, условные переходы и эффект наблюдателя. Также упоминается о наблюдении производительности программ и оптимизации через постоянное складывание.

1. Сложности микробенчмаркинга
Андрей Акиньшин, JetBrains
DevFest Siberia 2017, Новосибирск, 24.09.2017
1/52

2. Часть 1
Почему мы об этом говорим?
2/52 1. Почему мы об этом говорим?

3. StackOverflow
Люди любят бенчмаркать
3/52 1. Почему мы об этом говорим?

4. StackOverflow
Типичный вопрос
4/52 1. Почему мы об этом говорим?

5. Habrahabr
Некоторые делают выводы и пишут статьи
5/52 1. Почему мы об этом говорим?

6. Из интернетов
6/52 1. Почему мы об этом говорим?

7. Из интернетов
6/52 1. Почему мы об этом говорим?

8. Из интернетов
6/52 1. Почему мы об этом говорим?

9. Применения бенчмарков
7/52 1. Почему мы об этом говорим?

10. Применения бенчмарков
• Performance analysis
• Сравнение алгоритмов
• Оценка улучшений производительности
• Анализ регрессии
• . . .
7/52 1. Почему мы об этом говорим?

11. Применения бенчмарков
• Performance analysis
• Сравнение алгоритмов
• Оценка улучшений производительности
• Анализ регрессии
• . . .
• Научный интерес
7/52 1. Почему мы об этом говорим?

12. Применения бенчмарков
• Performance analysis
• Сравнение алгоритмов
• Оценка улучшений производительности
• Анализ регрессии
• . . .
• Научный интерес
• Маркетинг
7/52 1. Почему мы об этом говорим?

13. Применения бенчмарков
• Performance analysis
• Сравнение алгоритмов
• Оценка улучшений производительности
• Анализ регрессии
• . . .
• Научный интерес
• Маркетинг
• Весёлое времяпрепровождение
7/52 1. Почему мы об этом говорим?

14. Сегодня в программе
• Увлекательные микробенчмарки на C#.
8/52 1. Почему мы об этом говорим?

15. Сегодня в программе
• Увлекательные микробенчмарки на C#.
∗ Слушатели с хорошим воображением легко перенесут основные
выводы на все остальные языки и рантаймы.
8/52 1. Почему мы об этом говорим?

16. Часть 2
Количество итераций
9/52 2. Количество итераций

17. Микробенчмаркинг
Плохой бенчмарк
// Resolution(Stopwatch) = 466 ns
// Latency(Stopwatch) = 18 ns
var sw = Stopwatch.StartNew();
Foo(); // 100 ns
sw.Stop();
WriteLine(sw.ElapsedMilliseconds);
10/52 2. Количество итераций

18. Микробенчмаркинг
Плохой бенчмарк
// Resolution(Stopwatch) = 466 ns
// Latency(Stopwatch) = 18 ns
var sw = Stopwatch.StartNew();
Foo(); // 100 ns
sw.Stop();
WriteLine(sw.ElapsedMilliseconds);
Небольшое улучшение
var sw = Stopwatch.StartNew();
for (int i = 0; i < N; i++) // (N * 100 + eps) ns
Foo();
sw.Stop();
var total = sw.ElapsedTicks / Stopwatch.Frequency;
WriteLine(total / N);
10/52 2. Количество итераций

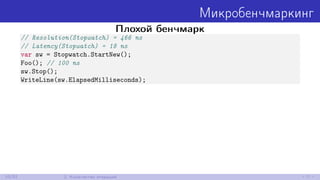
19. Прогрев
Запустим бенчмарк несколько раз:
int[] x = new int[128 * 1024 * 1024];
for (int iter = 0; iter < 5; iter++)
{
var sw = Stopwatch.StartNew();
for (int i = 0; i < x.Length; i += 16)
x[i]++;
sw.Stop();
Console.WriteLine(sw.ElapsedMilliseconds);
}
11/52 2. Количество итераций

20. Прогрев
Запустим бенчмарк несколько раз:
int[] x = new int[128 * 1024 * 1024];
for (int iter = 0; iter < 5; iter++)
{
var sw = Stopwatch.StartNew();
for (int i = 0; i < x.Length; i += 16)
x[i]++;
sw.Stop();
Console.WriteLine(sw.ElapsedMilliseconds);
}
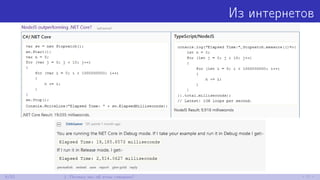
Результат:
176
81
62
62
62
11/52 2. Количество итераций

21. Несколько запусков метода
Run 01 : 529.8674 ns/op
Run 02 : 532.7541 ns/op
Run 03 : 558.7448 ns/op
Run 04 : 555.6647 ns/op
Run 05 : 539.6401 ns/op
Run 06 : 539.3494 ns/op
Run 07 : 564.3222 ns/op
Run 08 : 551.9544 ns/op
Run 09 : 550.1608 ns/op
Run 10 : 533.0634 ns/op
12/52 2. Количество итераций

22. Несколько запусков бенчмарка
13/52 2. Количество итераций

23. Простой случай
Центральная предельная теорема
спешит на помощь!
14/52 2. Количество итераций

24. Но есть и сложные случаи
15/52 2. Количество итераций

25. Часть 3
Работаем с памятью
16/52 3. Работаем с памятью

26. Сумма элементов массива
const int N = 1024;
int[,] a = new int[N, N];
[Benchmark]
public double SumIj()
{
var sum = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
sum += a[i, j];
return sum;
}
[Benchmark]
public double SumJi()
{
var sum = 0;
for (int j = 0; j < N; j++)
for (int i = 0; i < N; i++)
sum += a[i, j];
return sum;
}
17/52 3. Работаем с памятью

27. Сумма элементов массива
const int N = 1024;
int[,] a = new int[N, N];
[Benchmark]
public double SumIj()
{
var sum = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
sum += a[i, j];
return sum;
}
[Benchmark]
public double SumJi()
{
var sum = 0;
for (int j = 0; j < N; j++)
for (int i = 0; i < N; i++)
sum += a[i, j];
return sum;
}
SumIj SumJi
LegacyJIT-x86 ≈1.3ms ≈4.0ms
17/52 3. Работаем с памятью

28. CPU Cache
18/52 3. Работаем с памятью

29. Часть 4
Работаем с условными переходами
19/52 4. Работаем с условными переходами

30. Branch prediction
const int N = 32767;
int[] sorted, unsorted; // random numbers [0..255]
private static int Sum(int[] data)
{
int sum = 0;
for (int i = 0; i < N; i++)
if (data[i] >= 128)
sum += data[i];
return sum;
}
[Benchmark]
public int Sorted()
{
return Sum(sorted);
}
[Benchmark]
public int Unsorted()
{
return Sum(unsorted);
}
20/52 4. Работаем с условными переходами

31. Branch prediction
const int N = 32767;
int[] sorted, unsorted; // random numbers [0..255]
private static int Sum(int[] data)
{
int sum = 0;
for (int i = 0; i < N; i++)
if (data[i] >= 128)
sum += data[i];
return sum;
}
[Benchmark]
public int Sorted()
{
return Sum(sorted);
}
[Benchmark]
public int Unsorted()
{
return Sum(unsorted);
}
Sorted Unsorted
LegacyJIT-x86 ≈20µs ≈139µs
20/52 4. Работаем с условными переходами

32. Часть 5
Observer effect
21/52 5. Observer effect

33. Загадка
Вопрос. Какая программа работает намного медленнее
остальных?
const int N = 100001;
public double Sum()
{
double x = 1, y = 1;
for (int i = 0; i < N; i++)
x = x + y;
return x;
}
// A
Sum();
// B
Write(Stopwatch.Frequency);
Sum();
22/52 5. Observer effect

34. Загадка
Вопрос. Какая программа работает намного медленнее
остальных?
const int N = 100001;
public double Sum()
{
double x = 1, y = 1;
for (int i = 0; i < N; i++)
x = x + y;
return x;
}
// A
Sum();
// B
Write(Stopwatch.Frequency);
Sum();
const int N = 100001;
public double Sum2()
{
double x = 1, y = 1;
var sw = Stopwatch.StartNew();
for (int i = 0; i < N; i++)
x = x + y;
sw.Stop();
return x;
}
// C
Sum2();
// D
Write(Stopwatch.Frequency);
Sum2();
22/52 5. Observer effect

35. Загадка
Вопрос. Какая программа работает намного медленнее
остальных?
const int N = 100001;
public double Sum()
{
double x = 1, y = 1;
for (int i = 0; i < N; i++)
x = x + y;
return x;
}
// A
Sum();
// B
Write(Stopwatch.Frequency);
Sum();
const int N = 100001;
public double Sum2()
{
double x = 1, y = 1;
var sw = Stopwatch.StartNew();
for (int i = 0; i < N; i++)
x = x + y;
sw.Stop();
return x;
}
// C
Sum2();
// D
Write(Stopwatch.Frequency);
Sum2();
Ответ. Если используется LegacyJIT-x86, то программа C:
A B C D
LegacyJIT-x86 ≈100µs ≈100µs ≈335µs ≈100µs
22/52 5. Observer effect

36. Отгадка
// D
// Статический конструктор класса
// Stopwatch вызывается при
// обращении к Stopwatch.Frequency
Write(Stopwatch.Frequency);
// Поэтому нам не нужно
// вызывать его из метода.
Sum2();
23/52 5. Observer effect

37. Отгадка
// D
// Статический конструктор класса
// Stopwatch вызывается при
// обращении к Stopwatch.Frequency
Write(Stopwatch.Frequency);
// Поэтому нам не нужно
// вызывать его из метода.
Sum2();
// C
// Статический конструктор класса
// Stopwatch ещё не вызывался.
// Поэтому нам придётся
// вызвать его из метода.
Sum2();
23/52 5. Observer effect

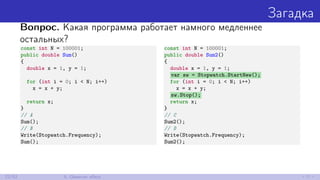
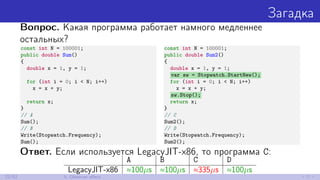
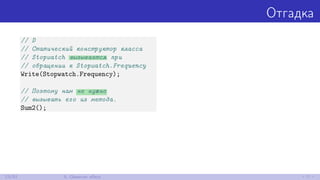
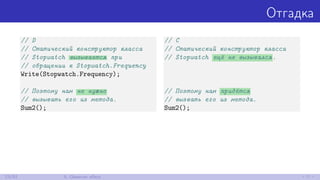
38. Отгадка
// D
// Статический конструктор класса
// Stopwatch вызывается при
// обращении к Stopwatch.Frequency
Write(Stopwatch.Frequency);
// Поэтому нам не нужно
// вызывать его из метода.
Sum2();
// C
// Статический конструктор класса
// Stopwatch ещё не вызывался.
// Поэтому нам придётся
// вызвать его из метода.
Sum2();
; x + y (A, B, D)
fld1
faddp st(1),st
; x + y (C)
fld1
fadd qword ptr [ebp-0Ch]
fstp qword ptr [ebp-0Ch]
23/52 5. Observer effect

39. Часть 6
Constant folding
24/52 6. Constant folding

40. Учимся извлекать корни
double Sqrt13() =>
Math.Sqrt(1) + Math.Sqrt(2) + Math.Sqrt(3) + /* ... */
+ Math.Sqrt(13);
VS
double Sqrt14() =>
Math.Sqrt(1) + Math.Sqrt(2) + Math.Sqrt(3) + /* ... */
+ Math.Sqrt(13) + Math.Sqrt(14);
25/52 6. Constant folding

41. Учимся извлекать корни
double Sqrt13() =>
Math.Sqrt(1) + Math.Sqrt(2) + Math.Sqrt(3) + /* ... */
+ Math.Sqrt(13);
VS
double Sqrt14() =>
Math.Sqrt(1) + Math.Sqrt(2) + Math.Sqrt(3) + /* ... */
+ Math.Sqrt(13) + Math.Sqrt(14);
RyuJIT-x64
Sqrt13 ≈91ns
Sqrt14 0 ns
25/52 6. Constant folding

42. Как же так?
RyuJIT-x64, Sqrt13
vsqrtsd xmm0,xmm0,mmword ptr [7FF94F9E4D28h]
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D30h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D38h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D40h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D48h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D50h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D58h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D60h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D68h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D70h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D78h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D80h]
vaddsd xmm0,xmm0,xmm1
vsqrtsd xmm1,xmm0,mmword ptr [7FF94F9E4D88h]
vaddsd xmm0,xmm0,xmm1
ret
26/52 6. Constant folding

43. Как же так?
RyuJIT-x64, Sqrt14
vmovsd xmm0,qword ptr [7FF94F9C4C80h]
ret
27/52 6. Constant folding

44. Как же так?
Большое дерево выражения* stmtExpr void (top level) (IL 0x000... ???)
| /--* mathFN double sqrt
| | --* dconst double 13.000000000000000
| /--* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 12.000000000000000
| | --* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 11.000000000000000
| | --* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 10.000000000000000
| | --* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 9.0000000000000000
| | --* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 8.0000000000000000
| | --* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 7.0000000000000000
| | --* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 6.0000000000000000
| | --* + double
| | | /--* mathFN double sqrt
| | | | --* dconst double 5.0000000000000000
// ...
28/52 6. Constant folding

45. Как же так?
Constant folding в действии
N001 [000001] dconst 1.0000000000000000 => $c0 {DblCns[1.000000]}
N002 [000002] mathFN => $c0 {DblCns[1.000000]}
N003 [000003] dconst 2.0000000000000000 => $c1 {DblCns[2.000000]}
N004 [000004] mathFN => $c2 {DblCns[1.414214]}
N005 [000005] + => $c3 {DblCns[2.414214]}
N006 [000006] dconst 3.0000000000000000 => $c4 {DblCns[3.000000]}
N007 [000007] mathFN => $c5 {DblCns[1.732051]}
N008 [000008] + => $c6 {DblCns[4.146264]}
N009 [000009] dconst 4.0000000000000000 => $c7 {DblCns[4.000000]}
N010 [000010] mathFN => $c1 {DblCns[2.000000]}
N011 [000011] + => $c8 {DblCns[6.146264]}
N012 [000012] dconst 5.0000000000000000 => $c9 {DblCns[5.000000]}
N013 [000013] mathFN => $ca {DblCns[2.236068]}
N014 [000014] + => $cb {DblCns[8.382332]}
N015 [000015] dconst 6.0000000000000000 => $cc {DblCns[6.000000]}
N016 [000016] mathFN => $cd {DblCns[2.449490]}
N017 [000017] + => $ce {DblCns[10.831822]}
N018 [000018] dconst 7.0000000000000000 => $cf {DblCns[7.000000]}
N019 [000019] mathFN => $d0 {DblCns[2.645751]}
N020 [000020] + => $d1 {DblCns[13.477573]}
...
29/52 6. Constant folding

46. Часть 7
CPU Cache Associativity
30/52 7. CPU Cache Associativity

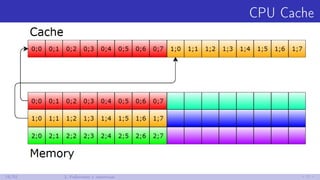
47. Ещё один весёлый пример
private int[,] a;
[Params(511, 512, 513)] public int N;
[Setup] public void Setup() => a = new int[N, N];
// Ищем максимальный элемент в колонке
[Benchmark] public int Max() {
int max = 0;
for (int i = 0; i < N; i++)
max = Math.Max(max, a[i, 0]);
return max;
}
∗
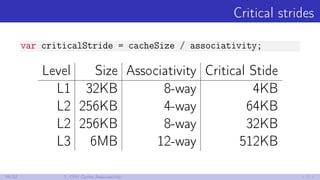
Windows 10, .NET 4.6.2, LegacyJIT-x86, Skylake
31/52 7. CPU Cache Associativity

48. Результаты зависят от N
N Max
511 ≈844ns
512 ≈1330ns
513 ≈844ns
32/52 7. CPU Cache Associativity

49. Немножко теории
33/52 7. CPU Cache Associativity

50. Critical strides
var criticalStride = cacheSize / associativity;
34/52 7. CPU Cache Associativity

51. Critical strides
var criticalStride = cacheSize / associativity;
Level Size Associativity Critical Stide
L1 32KB 8-way 4KB
L2 256KB 4-way 64KB
L2 256KB 8-way 32KB
L3 6MB 12-way 512KB
34/52 7. CPU Cache Associativity

52. Минутка занимательного про Skylake
Почитаем Intel® 64 and IA-32 Architectures Optimization Reference Manual:
2.1.3. THE SKYLAKE MICROARCHITECTURE: Cache and Memory Subsystem
• Simultaneous handling of more loads and stores enabled by enlarged
buffers.
• Page split load penalty down from 100 cycles in previous generation
to 5 cycles.
• L3 write bandwidth increased from 4 cycles per line in previous
generation to 2 per line.
• L2 associativity changed from 8 ways to 4 ways.
35/52 7. CPU Cache Associativity

53. Часть 8
Выравнивание
36/52 8. Выравнивание

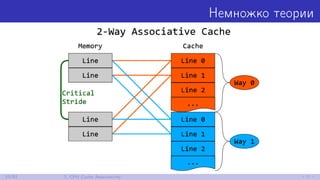
54. Очень простые структурки
public struct Struct3 {
public byte X1, X2, X3;
}
public struct Struct8 {
public byte X1, X2, X3, X4, X5, X6, X7, X8;
}
private Struct3[] struct3 = new Struct3[256];
private Struct8[] struct8 = new Struct8[256];
37/52 8. Выравнивание

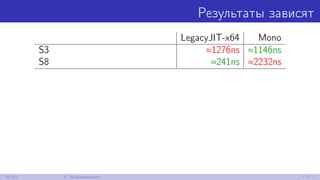
55. Очень простой бенчмарк
[Benchmark] public int S3() {
int res = 0;
for (int i = 0; i < struct3.Length; i++) {
var s = struct3[i]; res += s.X1 + s.X2;
}
return res;
}
[Benchmark] public int S8() {
int res = 0;
for (int i = 0; i < struct8.Length; i++) {
var s = struct8[i]; res += s.X1 + s.X2;
}
return res;
}
38/52 8. Выравнивание

56. Результаты зависят
LegacyJIT-x64 Mono
S3 ≈1276ns ≈1146ns
S8 ≈241ns ≈2232ns
39/52 8. Выравнивание

57. Результаты зависят
LegacyJIT-x64 Mono
S3 ≈1276ns ≈1146ns
S8 ≈241ns ≈2232ns
Marshal.SizeOf(typeof(S3)) 3 8
39/52 8. Выравнивание

58. Тот же самый бенчмарк
// А что будет под RyuJIT-x64?
[Benchmark] public int S3() {
int res = 0;
for (int i = 0; i < struct3.Length; i++) {
var s = struct3[i]; res += s.X1 + s.X2;
}
return res;
}
[Benchmark] public int S8() {
int res = 0;
for (int i = 0; i < struct8.Length; i++) {
var s = struct8[i]; res += s.X1 + s.X2;
}
return res;
}
40/52 8. Выравнивание

59. Внезапные результаты
RyuJIT-x64
S3 ≈280ns
S8 ≈280ns
41/52 8. Выравнивание

60. Смотрим ASM
; *** S3 ***
; res += s.X1 + s.X2;
add eax, r10d
add eax, r9d
; *** S8 ***
; res += s.X1 + s.X2;
movzx r9d, byte ptr [rsp+20h]
add eax, r9d
movzx r9d, byte ptr [rsp+21h]
add eax, r9d
42/52 8. Выравнивание

61. (Текущая реализация) Struct promotion
Иногда RyuJIT1 может аллоцировать структуру
в регистрах, а не на стеке
• The struct must not be address-taken.
• It must have no overlapping fields.
• It must have only primitive fields.
• It must not be an argument or a return value that is passed in
registers.
• It can’t be larger than 32 bytes.
• It can’t have more than 4 fields.
1
Справедливо для v4.6.1637.0, поведение может поменяться, см. coreclr#6733
43/52 8. Выравнивание

62. Часть 9
Заключение
44/52 9. Заключение

63. Хорошие инструменты
• BenchmarkDotNet для .NET
• JMH для Java
• google/benchmark для C++
• rbenchmark для R
• ...
45/52 9. Заключение

64. Хорошие инструменты
• BenchmarkDotNet для .NET
• JMH для Java
• google/benchmark для C++
• rbenchmark для R
• ...
∗ Если вы используете хороший инструмент, то это не означает,
что ваш бенчмарк тоже хороший.
45/52 9. Заключение

65. Методическая литература
Для успешных микробенчмарков нужно очень много знать.
Вот немного хороших книжек про .NET:
46/52 9. Заключение

66. Вопросы?
Андрей Акиньшин
http://aakinshin.net
https://github.com/AndreyAkinshin
https://twitter.com/andrey_akinshin
andrey.akinshin@gmail.com
47/52 9. Заключение