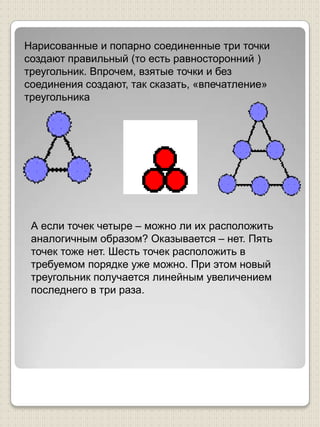
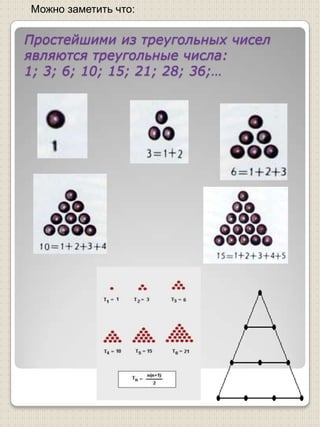
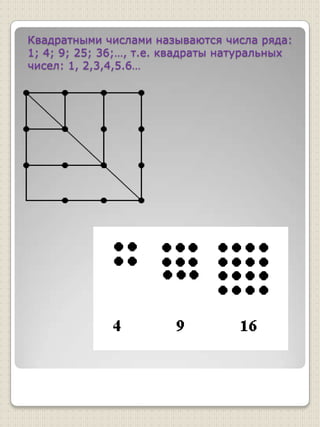
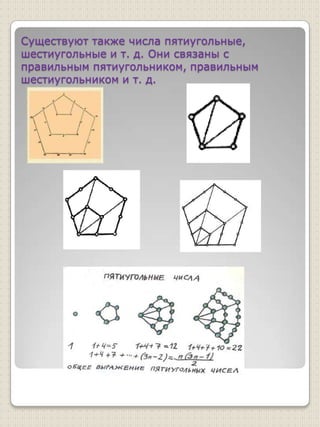
Документ описывает фигуры чисел и их связь с пифагорейским учением, подчеркивая важность чисел в философии Пифагора. Упоминаются треугольные, квадратные и другие многоугольные числа, а также их геометрические представления. Документ также затрагивает биографию Пифагора, его учебу и идеи о числе как основе всего существующего.

1. «Мозг, так же как и мускулы, развивается, когда его тренируют.» Фигурные числа

2. Цель работы: расширить знания о числах Задачи:узнать, какие числа называются фигурными;

3. изучить историю их возникновения;Из истории Пифагор – не только самый популярный ученый, но и самая загадочная личность, человек-символ, философ, пророк. Подлинную картину его жизни и достижений восстановить трудно, так как письменных документов о Пифагоре Самосском не осталось. Известно, что Пифагор родился на острове Самос в Эгейском море у берегов малой Азии около 570 г. до н. э. По многим античным свидетельствам родившийся мальчик был сказочно красив, а вскоре проявил и незаурядные способности. Увлекался музыкой и поэзией. Неугомонному воображению Пифагора очень скоро стало тесно на маленьком острове. Мудрый Ферекид – один из учителей Пифагора однажды сказал: «Ты вырос из Самоса, отправляйся путешествовать – только так ты утолишь жажду познаний. Помни: путешествие и память – суть два средства, возвышающие человека и открывающие ему врата мудрости». В основе религиозно-философского учения Пифагора лежало представление о числе, как основе всего существующего в мире. «Числа – суть боги на земле», – говорил он.

4. Из истории…Пифагорейцы составляли из костяшек или камешков различные фигуры, изображали числа в виде точек, группируемых в геометрические фигуры.Числа, которые возможно было представить с помощью геометрических фигур, получили в дальнейшем название фигурных

5. Нарисованные и попарно соединенные три точки создают правильный (то есть равносторонний ) треугольник. Впрочем, взятые точки и без соединения создают, так сказать, «впечатление» треугольникаА если точек четыре – можно ли их расположить аналогичным образом? Оказывается – нет. Пять точек тоже нет. Шесть точек расположить в требуемом порядке уже можно. При этом новый треугольник получается линейным увеличением последнего в три раза.

6. Чтобы впечатление треугольника сохранилось нужно добавить четыре точки. Соответствующий треугольник получается линейным увеличением исходного в три раза.Продолжая добавлять точки, будем получать все новые и новые треугольники.В приведенных примерах сначала точек было 3, 6, 10. Эти числа по вполне понятным причинам называются треугольными.

7. Можно заметить что: Простейшими из треугольных чисел являются треугольные числа:1; 3; 6; 10; 15; 21; 28; 36;…

8. В древности часто считали с помощью камешков и, естественно, отмечали случаи, когда камешки можно было сложить в виде правильной фигуры

9. Квадратными числами называются числа ряда: 1; 4; 9; 25; 36;…, т.е. квадраты натуральных чисел: 1, 2,3,4,5.6…

10. Существуют также числа пятиугольные, шестиугольные и т. д. Они связаны с правильным пятиугольником, правильным шестиугольником и т. д.

11. ИсточникиСавин А. П. и др. Я познаю мир. Математика. – М.;АСТ 1988. – 480с.Г.И.Глейзер история математики в школе. М.; «Просвещение» 1981www.wikipedia.ru