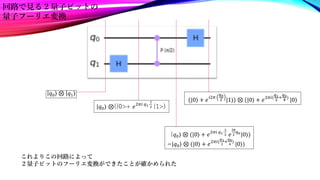
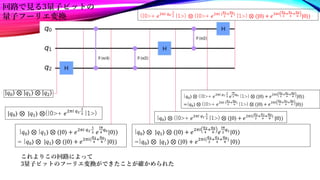
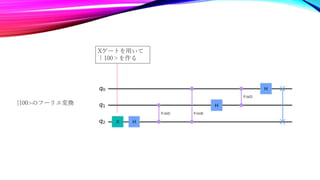
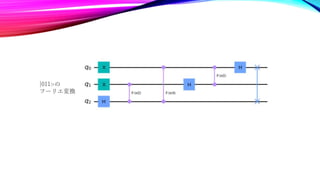
The document summarizes quantum Fourier transforms (QFTs) for 1, 2, and 3 qubit systems. It shows that a 1 qubit QFT is equivalent to a Hadamard gate. For 2 and 3 qubits, it represents the QFT formulas as quantum circuits, and verifies that they perform the Fourier transform by examining the state at each gate. The QFT generalizes the discrete Fourier transform to operate on quantum states, allowing it to be used in algorithms like Shor's algorithm.