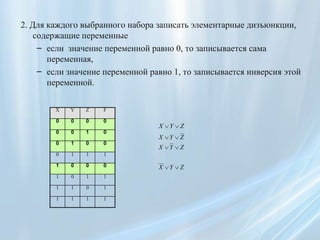
Документ описывает основы логических функций, включая простые и элементарные конъюнкции и дизъюнкции, а также их нормальные формы: конъюнктивную (КНФ) и дизъюнктивную (ДНФ). Приводятся алгоритмы построения совершенных форм (СКНФ и СДНФ) на основе таблицы истинности. Документ также включает примеры и необходимые условия для этих нормальных форм.

1. ДНФ, КНФ, СДНФ,
СКНФ
Санкт-Петербург
2012

2. Простые конъюнкции и дизъюнкции
• Простой конъюнкцией называется конъюнкция одной
или нескольких переменных, при этом каждая
переменная встречается не более одного раза (либо сама,
либо ее отрицание).
• Например, x&y&z является простой конъюнкцией.
• Простой дизъюнкцией называется дизъюнкция одной
или нескольких переменных, при этом каждая
переменная входит не более одного раза (либо сама, либо
ее отрицание).
• Например, выражение ¬xvyvz – простая дизъюнкция

3. Элементарные конъюнкции и
дизъюнкции
Элементарная конъюнкция Элементарная дизъюнкция –
– конъюнкция конечного дизъюнкция конечного множества
множества логических логических переменных и их
переменных и их инверсий. инверсий.
Ранг элементарной конъюнкции или дизъюнкции – число
аргументов ее образующих.
Примеры
Элементарная конъюнкция Элементарная дизъюнкция
третьего порядка второго порядка
F ( X ,Y , Z ) X Y Z F ( X ,Y ) X Y

4. КНФ и ДНФ
Нормальная форма логической функции – если
логическая функция представлена дизъюнкцией,
конъюнкцией и инверсией.
Конъюнктивная нормальная Дизъюнктивная нормальная
форма (КНФ) содержит форма (ДНФ) содержит
элементарные дизъюнкции, элементарные конъюнкции,
связанные между собой связанные между собой
операциями конъюнкции. операциями дизъюнкции.
Примеры
F ( X ,Y , Z ) ( X Z) (X Y Z) F ( X ,Y ) ( X Y ) (Y X)

5. СКНФ и СДНФ
Совершенная конъюнктивная Совершенная дизъюнктивная
нормальная форма (СКНФ): нормальная форма (СДНФ)
1) нет двух одинаковых 1) нет двух одинаковых
элементарных дизъюнкций; элементарных конъюнкций;
2) ни одна элементарная 2) ни одна элементарная
дизъюнкция не содержит двух конъюнкция не содержит двух
одинаковых переменных; одинаковых переменных;
3) ни одна элементарная 3) ни одна элементарная
дизъюнкция не содержит конъюнкция не содержит
переменную вместе с ее переменную вместе с ее
инверсией; инверсией;
4) все дизъюнкции имеют один 4) все конъюнкции имеют один
и тот же ранг. и тот же ранг.

6. Алгоритмы построения СКНФ и СДНФ
Алгоритм образования СКНФ и СДНФ по таблице истинности
1. Выделить в таблице истинности все 1. Выделить в таблице истинности все
строки, в которых функция принимает строки, в которых функция принимает
значения 0. значения 1.
2. Для каждого выбранного набора 2. Для каждого выбранного набора
записать элементарные дизъюнкции, записать элементарные конъюнкции,
содержащие переменные: содержащие переменные:
а) если значение переменной равно 0, а) если значение переменной равно 0,
то записывается сама переменная, то записывается инверсия этой
б) если значение переменной равно 1, переменной,
то записывается инверсия этой б) если значение переменной равно 1,
переменной. то записывается сама переменная.
3. Соединить элементарные 3. Соединить элементарные
дизъюнкции знаком конъюнкции. конъюнкции знаком дизъюнкции.

7. Пример
• Исходная таблица
X Y Z F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
1. Выделить в таблице истинности все строки, в которых функция
принимает значения 0.
X Y Z F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1

8. 2. Для каждого выбранного набора записать элементарные дизъюнкции,
содержащие переменные
– если значение переменной равно 0, то записывается сама
переменная,
– если значение переменной равно 1, то записывается инверсия этой
переменной.
X Y Z F
0 0 0 0
X Y Z
0 0 1 0
X Y Z
0 1 0 0
X Y Z
0 1 1 1
1 0 0 0 X Y Z
1 0 1 1
1 1 0 1
1 1 1 1

9. 3. Соединить элементарные дизъюнкции знаком конъюнкции.
F ( X ,Y , Z ) ( X Y Z) (X Y Z) (X Y Z) (X Y Z)

10. Использованные материалы:
• Гданский Н.И. Информатика. Профильный уровень:
практикум для 10-11 классов : в 2 ч. Ч. 1/ Н.И. Гданский,
А.В. Карпов. – М. : БИНОМ. Лаборатория знаний, 2012.
• http://www.mini-soft.ru/nstu/diskr/3_.php