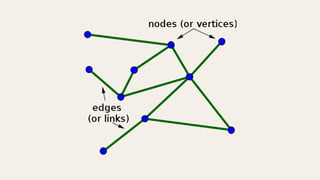
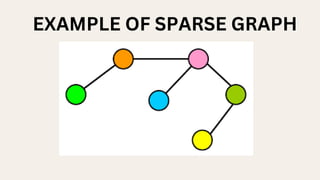
Sparse graphs have relatively few edges compared to vertices and are characterized by their efficiency in memory and computation. Algorithms such as BFS, DFS, Dijkstra's, and Kruskal's are effective for analyzing sparse graphs, making them suitable for large-scale applications in social networks, computer networks, and biological systems. Their advantages stem from reduced memory usage and optimized processing for scalability.

1. Sparse graph
Understanding
Sparse Graphs:
Concepts,
Characteristics,
and Applications

2. 01 - Introduction
02 - Graph Basics
03 -Dense graph
04 - Algorithms for
Sparse Graphs
05-Advantages of
Sparse Graphs

3. A sparse graph is a type of graph in
graph theory where the number of
edges is relatively small compared to
the number of vertices.
01 - Introduction

4. Vertices (or Nodes): The points in the
graph.
Edges (or Links): The connections
between the vertices.
02-Graph Basics

6. EXAMPLE OF SPARSE GRAPH

7. 03-Dense graph
A dense graph is a type of
graph in graph theory where
the number of edges is close
to the maximum possible
number of edges.

8. Dense graph Vs Sparse graph

9. Breadth-First Search (BFS) and Depth-First Search
(DFS)
Efficiently traverse sparse graphs.
Dijkstra's Algorithm
Finds shortest paths in weighted graphs; can be
optimized using data structures suited for sparsity.
Kruskal’s and Prim’s Algorithms
Find minimum spanning trees; Kruskal’s is
particularly efficient for sparse graphs.
Algorithms for Sparse Graphs

10. Advantages of Sparse Graphs
Memory Efficiency
Require less memory due to fewer edges.
Computational Efficiency
Many graph algorithms run faster on sparse graphs due
to fewer edges to process.
Scalability
Better suited for large-scale networks.

11. Applications of Sparse Graphs
Social Networks
Connections (friendships) are sparse compared to the total
number of possible connections.
Computer Networks
Routers and switches form sparse connections to optimize
performance and reduce costs.
Biological Networks
Protein-protein interaction networks where each protein
interacts with a few others.
Geographic Information Systems (GIS)
Road networks and public transportation maps are typically
sparse graphs.