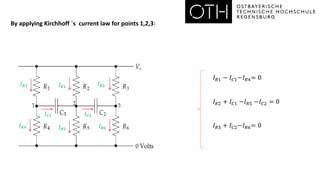
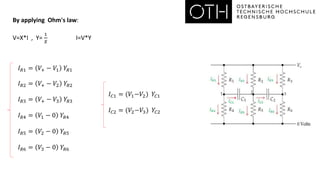
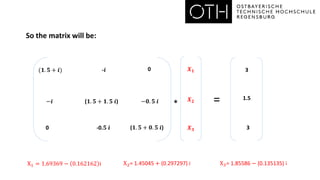
This document summarizes a presentation on solving linear systems of equations using Gaussian elimination. It includes the following: - An example linear system involving voltages (V1, V2, V3) and currents (I1-I6) in an electrical circuit with resistors and capacitors. - The steps to set up the linear system as a matrix equation involving the unknown voltages, including applying Kirchhoff's and Ohm's laws. 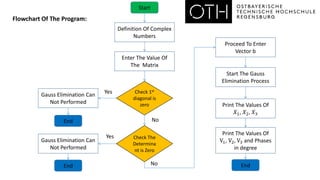- A flowchart showing the Gaussian elimination process: forming the augmented matrix, checking for zero diagonal/determinant, performing row operations if possible, and back substitution to solve for the unknowns. - The determinant calculation for the 3x3 matrix in this

1. Masters in Electrical & Microsystems
Engineering
Advanced Engineering Mathematics
Linear Systems Electric AC Circuit
Presented by:
Nima Aminfar (3362365)
Omer Rahama (3359754)

3. By applying Kirchhoff `s current law for points 1,2,3∶
𝐼𝑅4
𝐼𝑅1 𝐼𝑅2 𝐼𝑅3
𝐼𝑅5
𝐼𝑅6
𝐼𝐶1 𝐼𝐶2
𝐼𝑅1 − 𝐼𝐶1−𝐼𝑅4= 0
𝐼𝑅2 + 𝐼𝐶1 −𝐼𝑅5 −𝐼𝐶2 = 0
𝐼𝑅3 + 𝐼𝐶2−𝐼𝑅6= 0

4. 𝐼𝑅1 = 𝑉+ − 𝑉1 𝑌𝑅1
𝐼𝑅2 = 𝑉+ − 𝑉2 𝑌𝑅2
𝐼𝑅3 = 𝑉+ − 𝑉3 𝑌𝑅3
𝐼𝑅4 = 𝑉1 − 0 𝑌𝑅4
𝐼𝑅5 = 𝑉2 − 0 𝑌𝑅5
𝐼𝑅6 = 𝑉3 − 0 𝑌𝑅6
By applying Ohm's law:
V=X*I , Y=
1
𝑋
I=V*Y
𝐼𝐶1 = (𝑉1−𝑉2) 𝑌𝐶1
𝐼𝐶2 = (𝑉2−𝑉3) 𝑌𝐶2

5. 𝑉+ − 𝑉1 𝑌𝑅1 - (𝑉1−𝑉2) 𝑌𝐶1- 𝑉1 − 0 𝑌𝑅4 = 0
𝑉+ − 𝑉2 𝑌𝑅2 + (𝑉1−𝑉2) 𝑌𝐶1- 𝑉2 − 0 𝑌𝑅5 −(𝑉2−𝑉3) 𝑌𝐶2 = 0
𝑉+ − 𝑉3 𝑌𝑅3 + (𝑉2−𝑉3) 𝑌𝐶2 − 𝑉3 − 0 𝑌𝑅6 = 0
𝑉1 = 𝑋1 𝑒𝑖𝑤𝑡
𝑉2 = 𝑋2 𝑒𝑖𝑤𝑡
𝑉3 = 𝑋3 𝑒𝑖𝑤𝑡
𝑉+ = 𝑋+ 𝑒𝑖𝑤𝑡
And we know that :

6. 𝑌𝑅1 =
1
𝑋𝑅1
=
1
𝑅1
=
1
103 𝑌𝑅2 =
1
𝑋𝑅2
=
1
𝑅2
=
1
2∗103
𝑌𝑅3 =
1
𝑋𝑅3
=
1
𝑅3
=
1
103 𝑌𝑅4=
1
𝑋𝑅4
=
1
𝑅4
=
1
2∗103
𝑌𝑅5 =
1
𝑋𝑅5
=
1
𝑅5
=
1
103 𝑌𝑅6 =
1
𝑋𝑅6
=
1
𝑅6
=
1
2∗103
𝑌𝐶1 =
1
𝑋𝐶1
= 𝑖𝑤𝐶1 = 𝑖 ∗ 1000 ∗ 10−6
= 𝑖 ∗ 10−3
𝑌𝐶2 =
1
𝑋𝐶2
= 𝑖𝑤𝐶2 = 𝑖 ∗ 1000 ∗ 0.5 ∗ 10−6= 𝑖 ∗ 0.5 ∗ 10−3
Admittance Calculation:

7. Three linear equation would be: 𝑿𝟏 𝑿𝟐 𝑿𝟑 are unknown
(1.5 + 𝑖)*𝑋1 + (-i)*𝑋2 + (0)*𝑋3= 3
(−𝑖)*𝑋1 + (1.5 + 1.5 𝑖)*𝑋2 + (- 0.5 𝑖)*𝑋3= 1.5
0 ∗𝑋1 + ( − 0.5𝑖)∗𝑋2 + (1.5 + 0.5𝑖)∗𝑋3= 3

8. So the matrix will be:
=
*
(𝟏. 𝟓 + 𝒊)
X1 = 1.69369 − 0.162162 i
-𝒊
𝑿𝟐
0
𝑿𝟑
−𝒊 (𝟏. 𝟓 + 𝟏. 𝟓 𝒊) −𝟎. 𝟓 𝒊
0 -0.𝟓 𝒊 (𝟏. 𝟓 + 𝟎. 𝟓 𝒊)
3
1.5
3
𝑿𝟏
X2= 1.45045 + (0.297297) i X3= 1.85586 − (0.135135) i

9. Gaussian elimination Method:
• Gauss Elimination Method is a procedure for solving systems of linear equation. It is also known as Row
Reduction Technique.
• In this method, the problem of systems of linear equation having n unknown variables, matrix having rows
n and columns n+1 is formed. This matrix is also known as Augmented Matrix.
• After forming n x n+1 matrix, matrix is transformed to upper triangular matrix by row operations. Finally
result is obtained by Back Substitution.
• In this project, we are dealing with 3 unknown variables . So the Augmented Matrix would be 3*4.

10. Definition Of Complex
Numbers
Enter The Value Of
The Matrix
Check 1st
diagonal is
zero
Gauss Elimination Can
Not Performed
Check The
Determina
nt is Zero
Gauss Elimination Can
Not Performed
Start
End
End
Proceed To Enter
Vector b
Print The Values Of
V1, V2, V3 and Phases
in degree
Print The Values Of
𝑋1, 𝑋2, 𝑋3
End
Flowchart Of The Program:
Yes
Yes
No
No
Start The Gauss
Elimination Process

11. Determinant calculation for 3*3 Matrix: