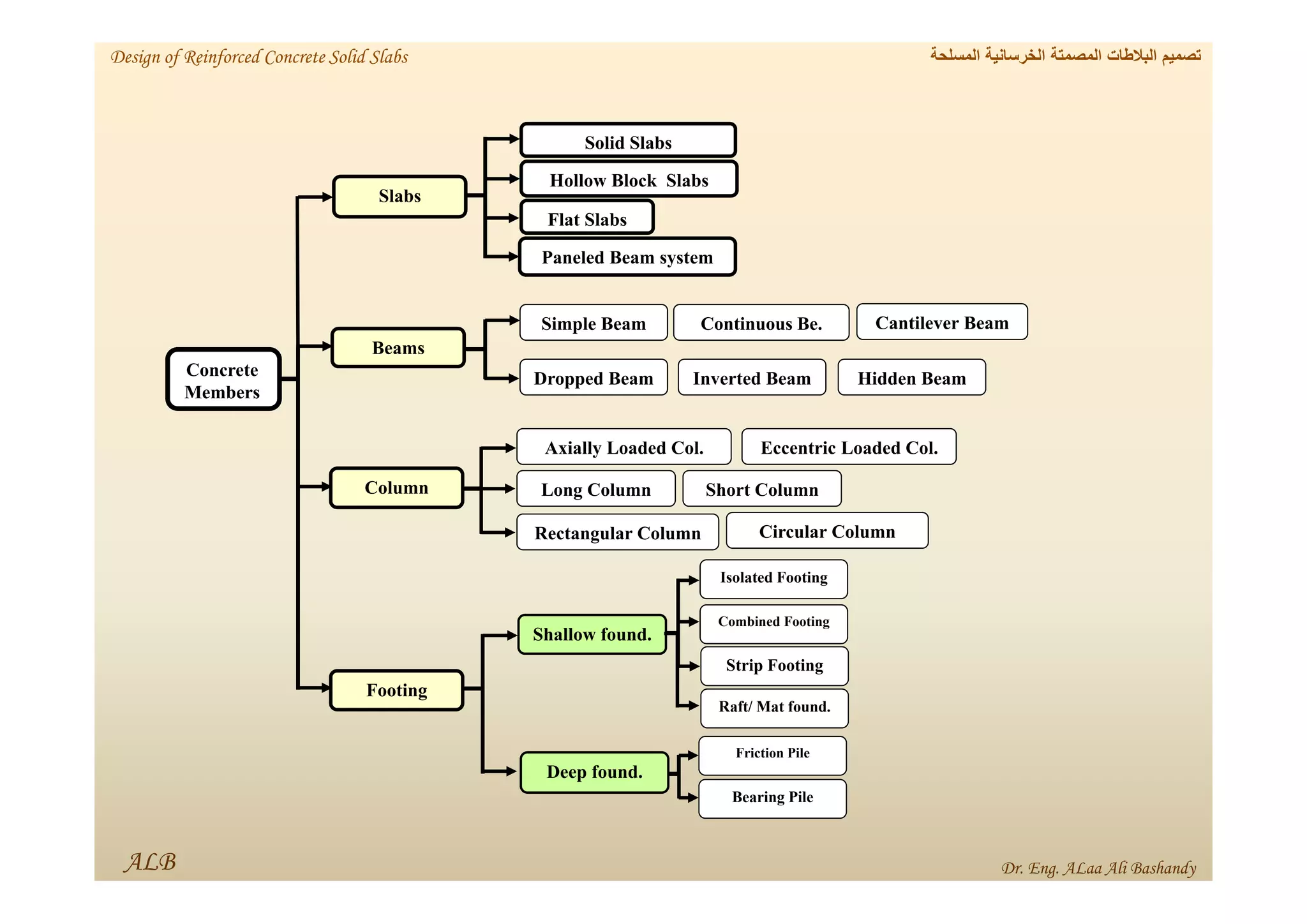
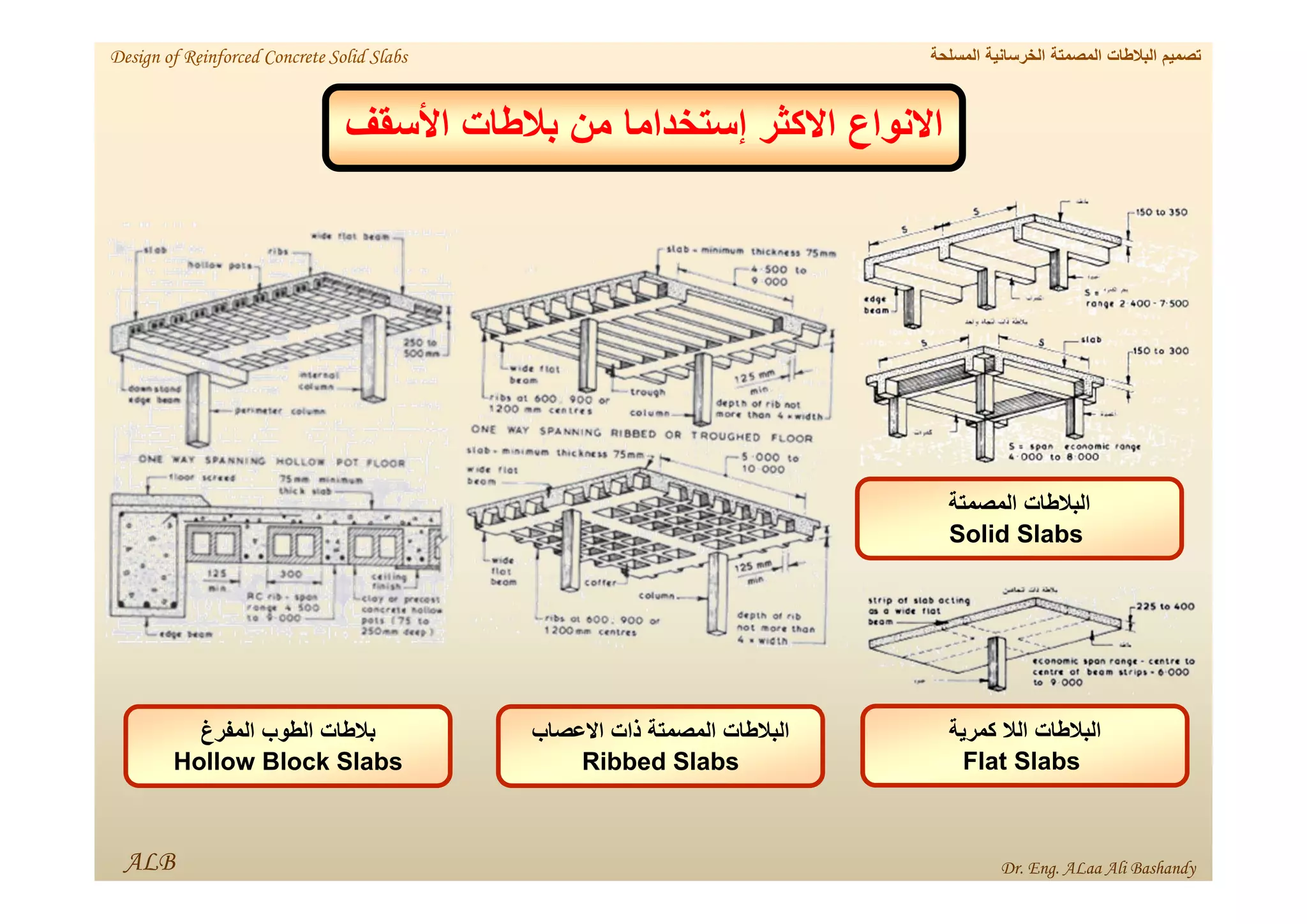
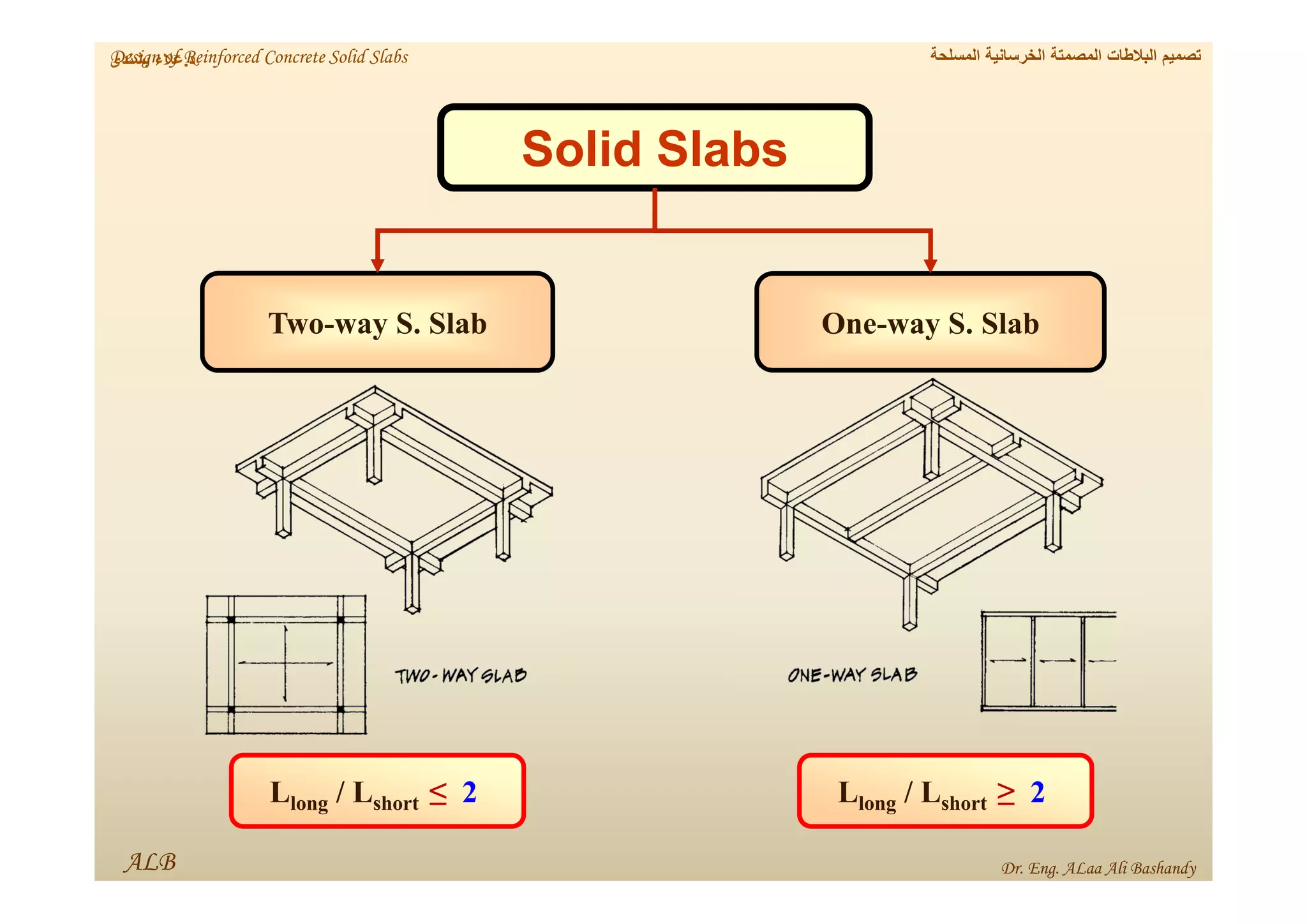
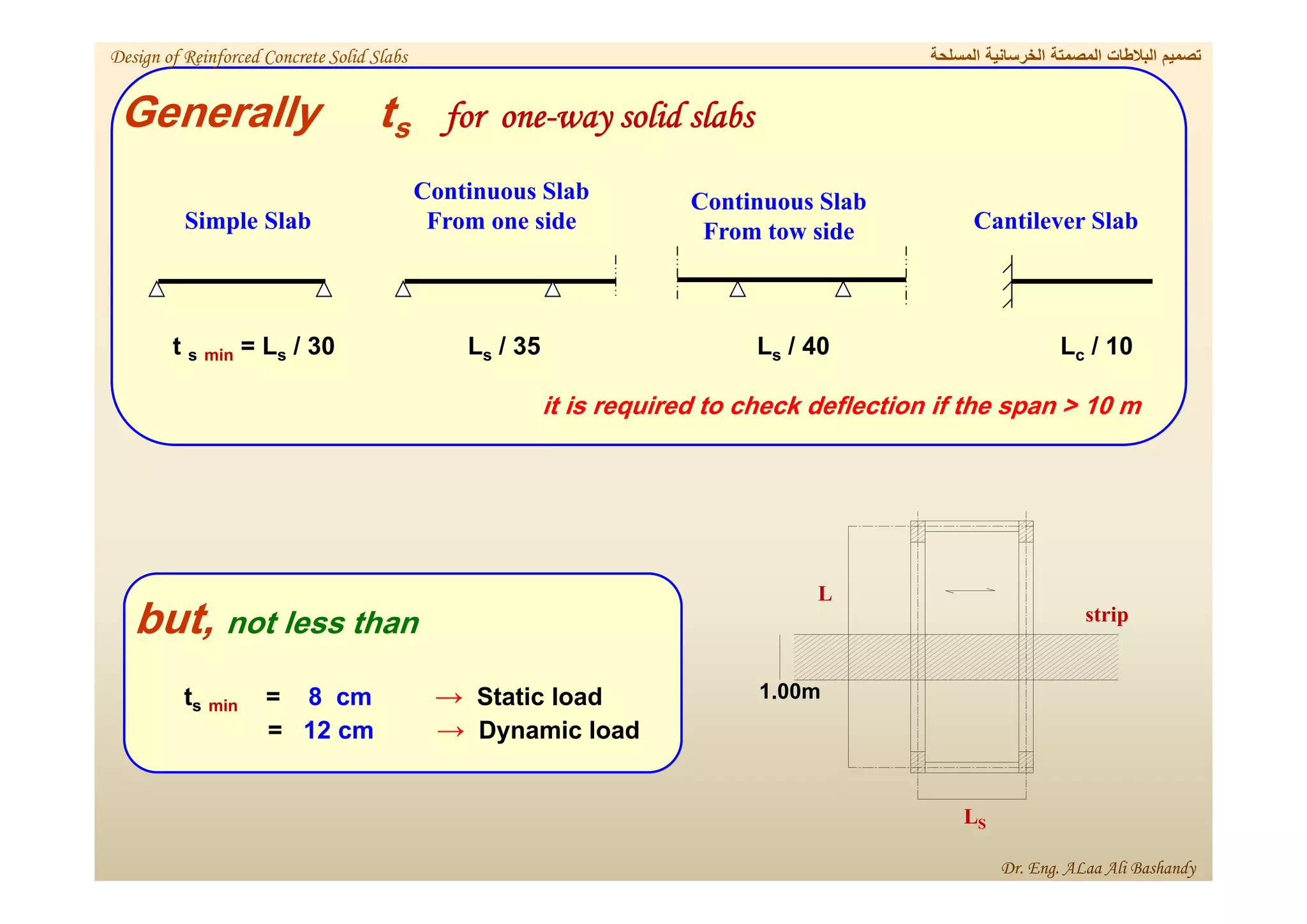
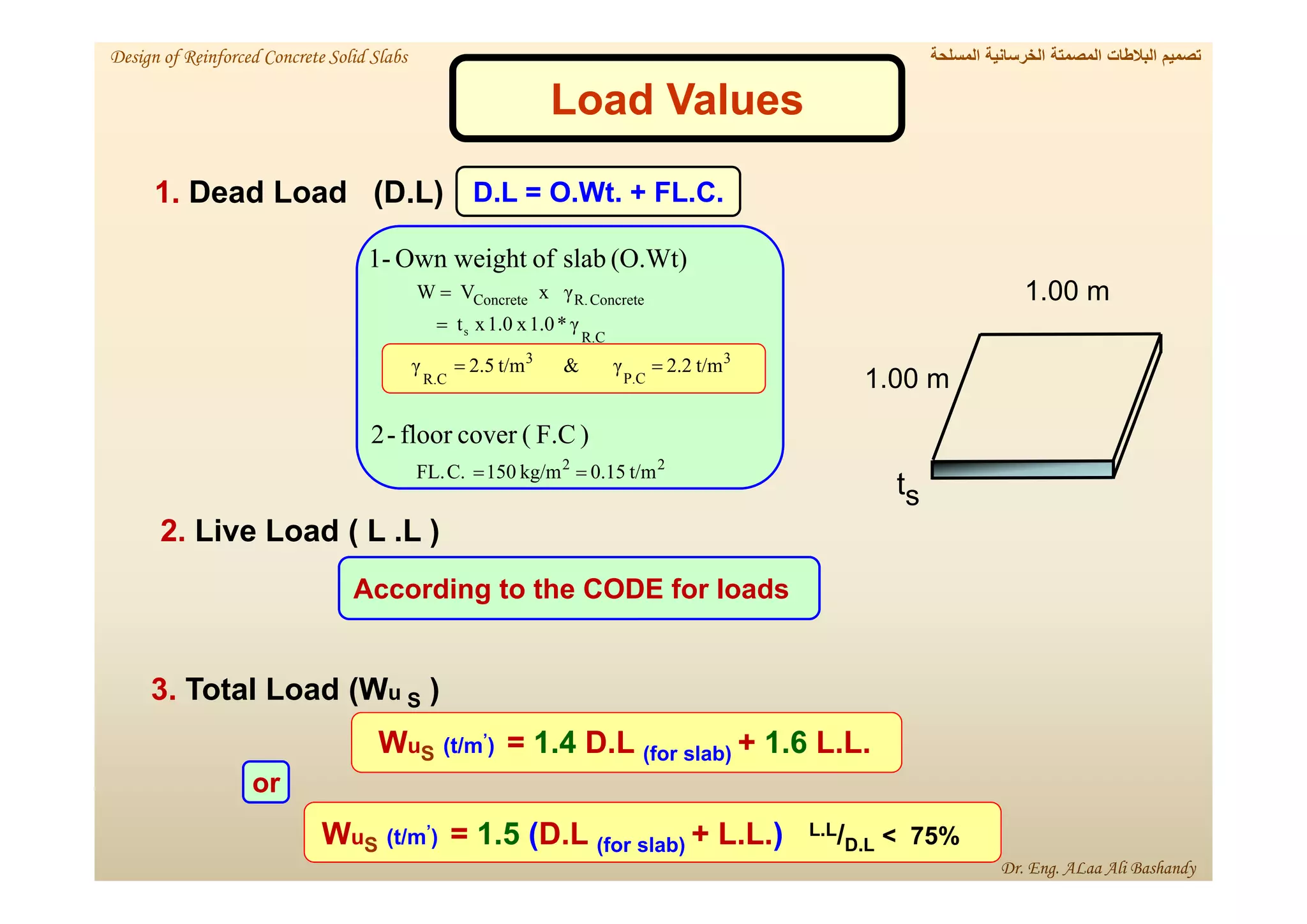
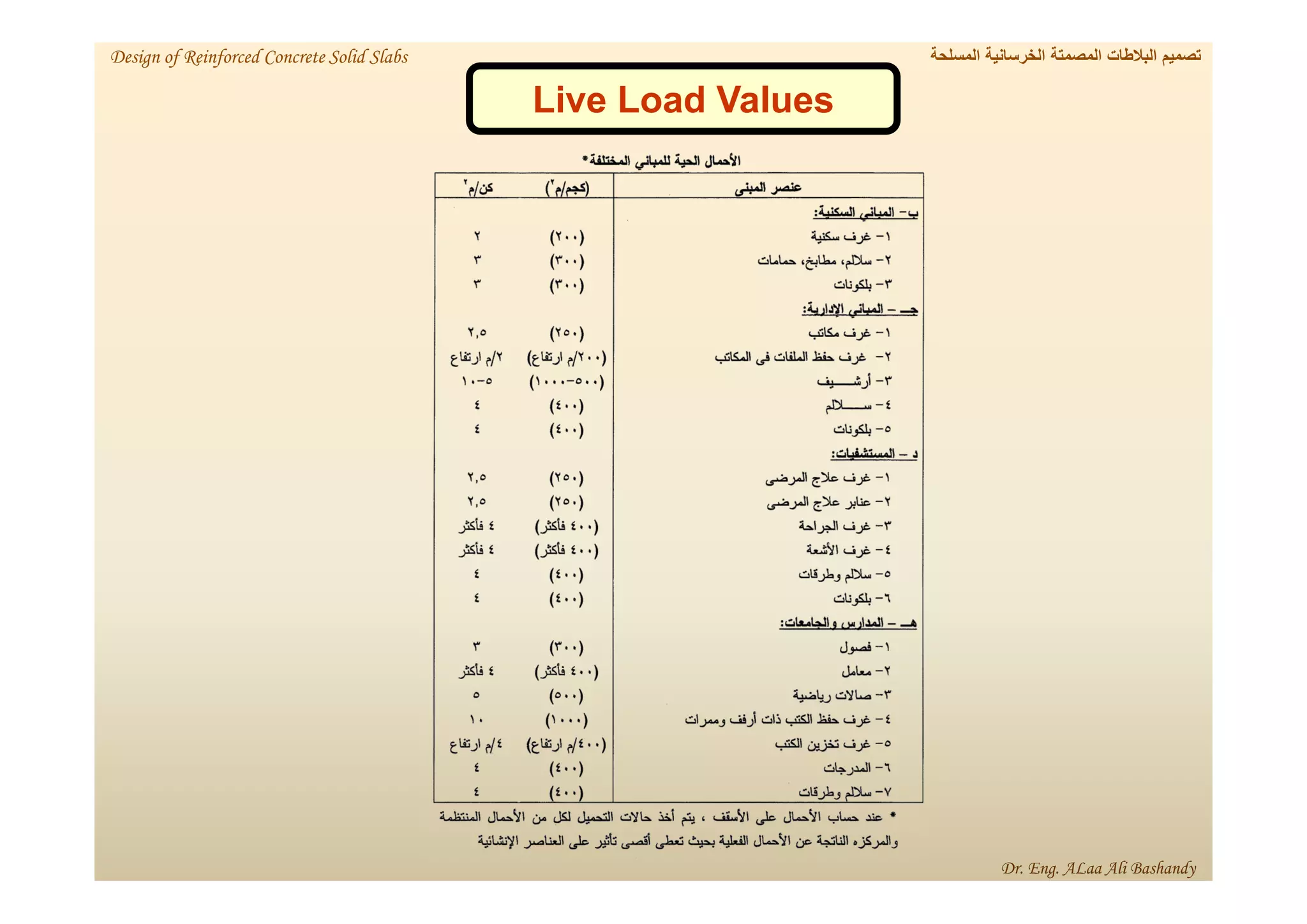
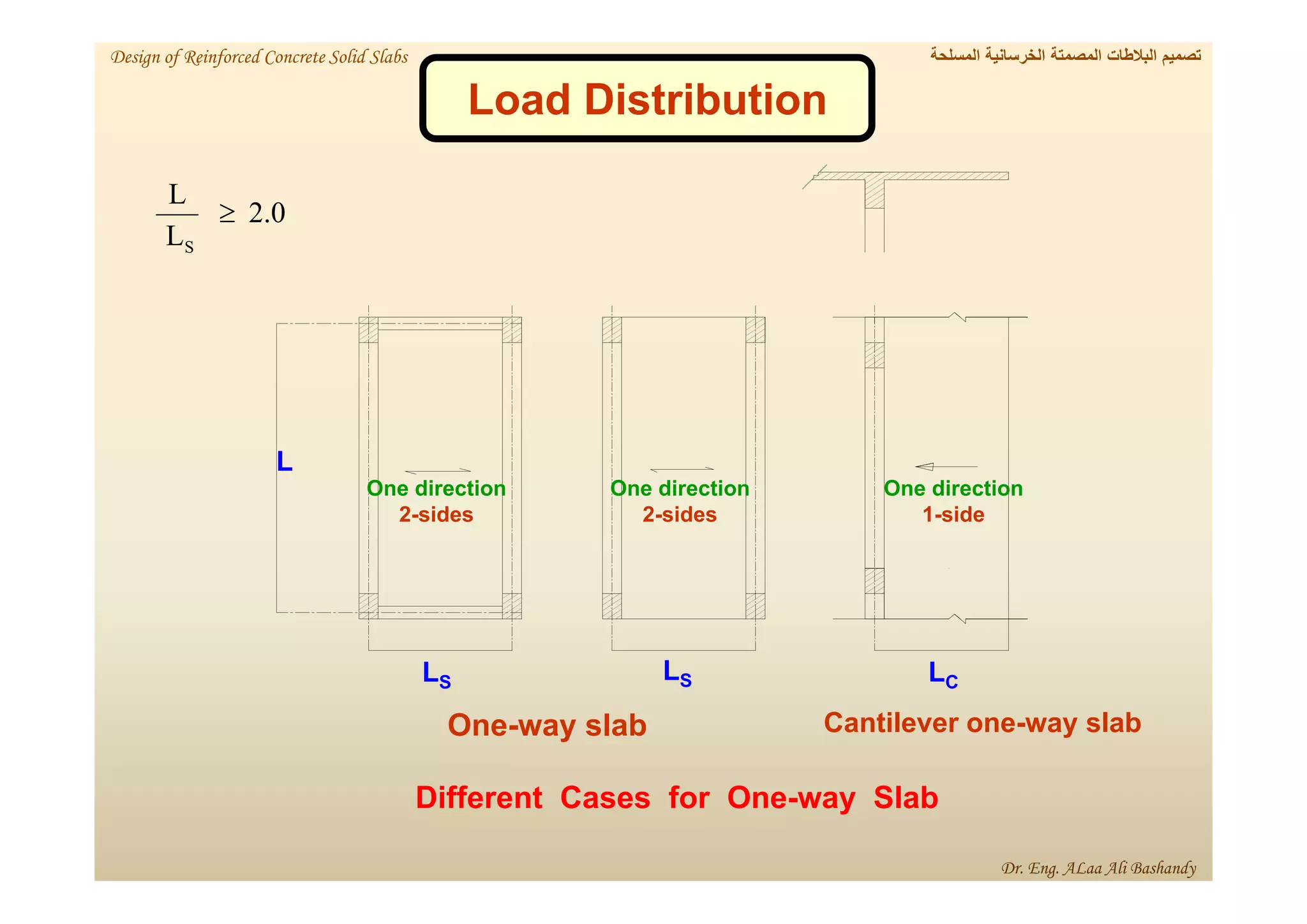
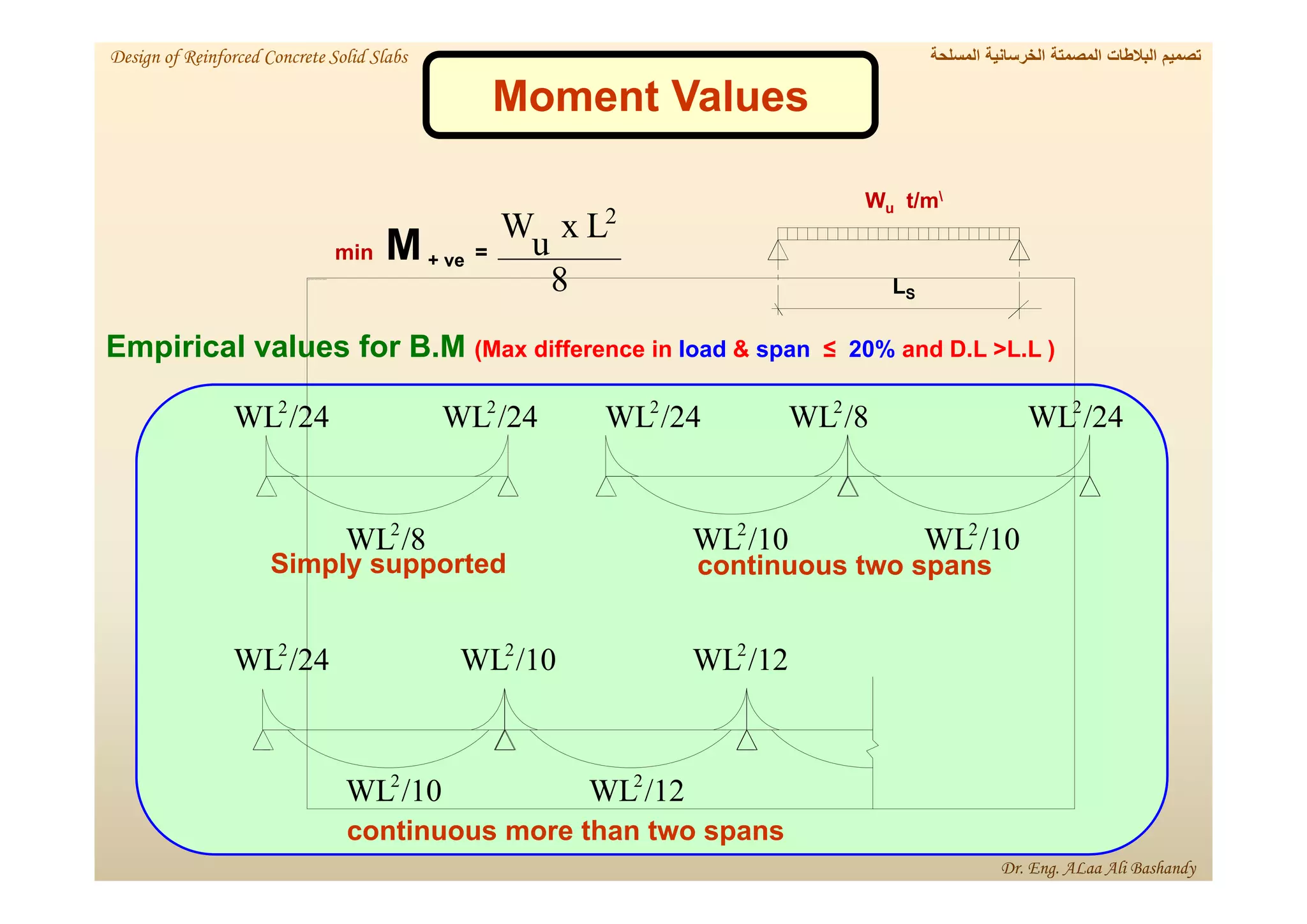
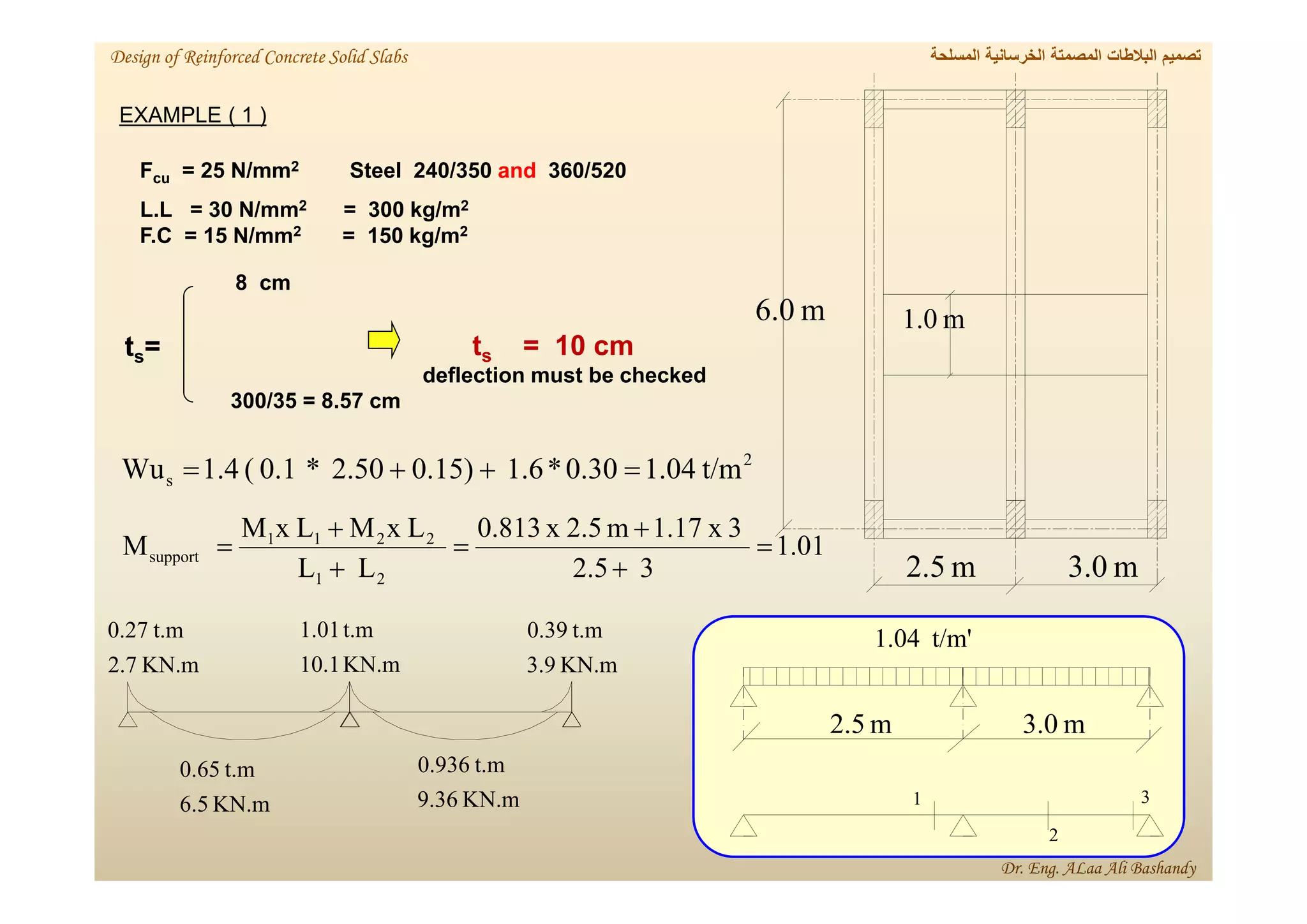
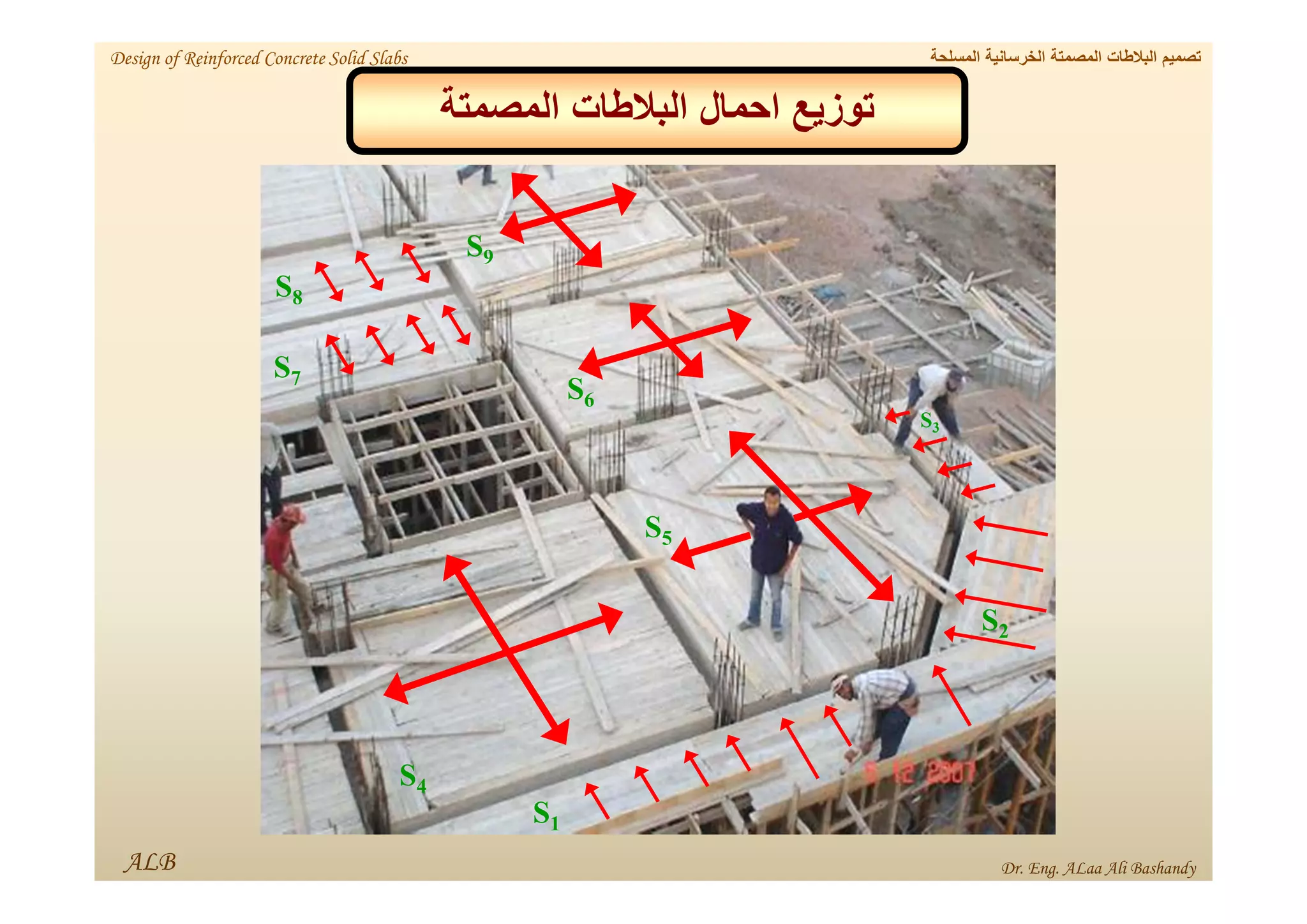
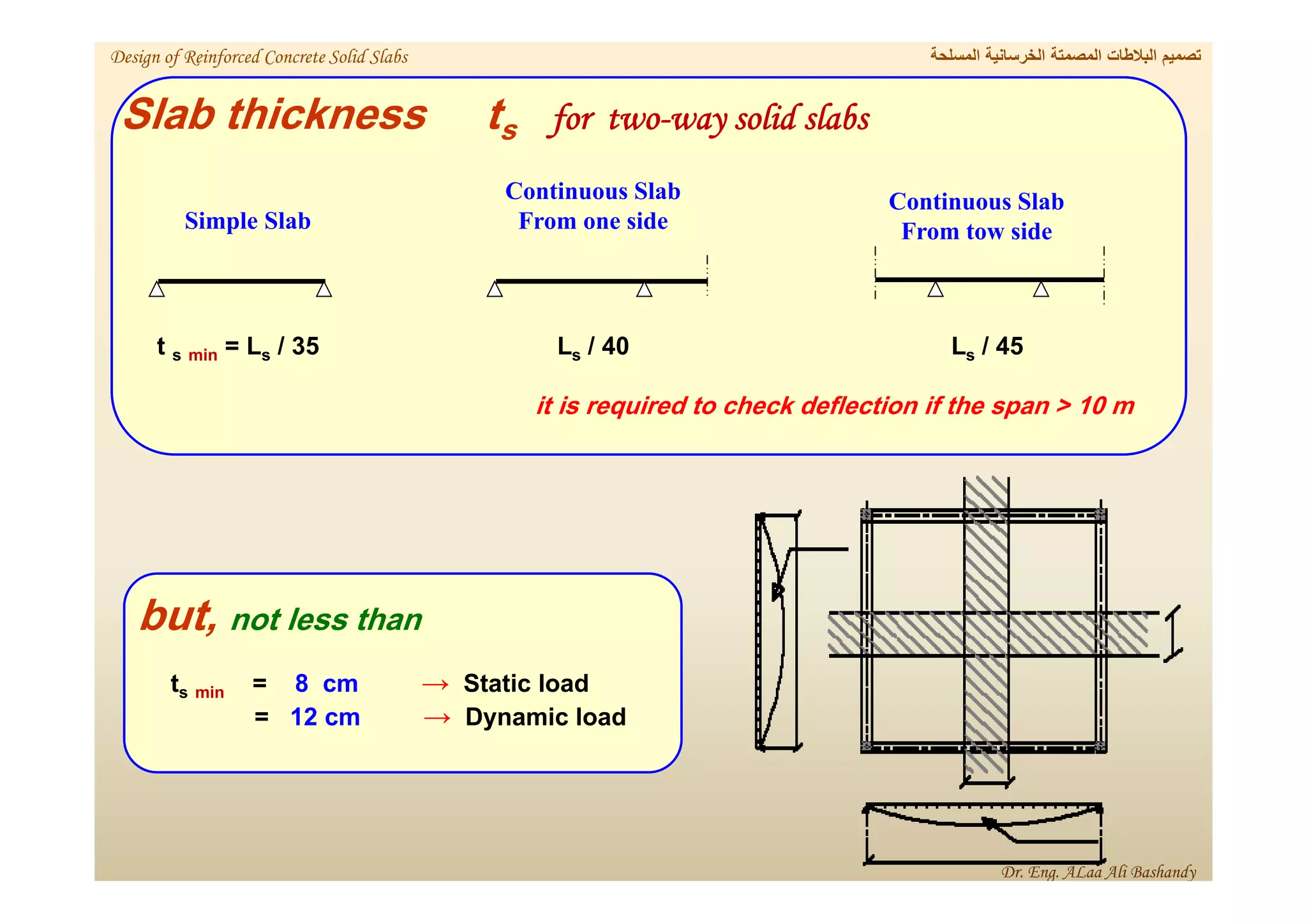
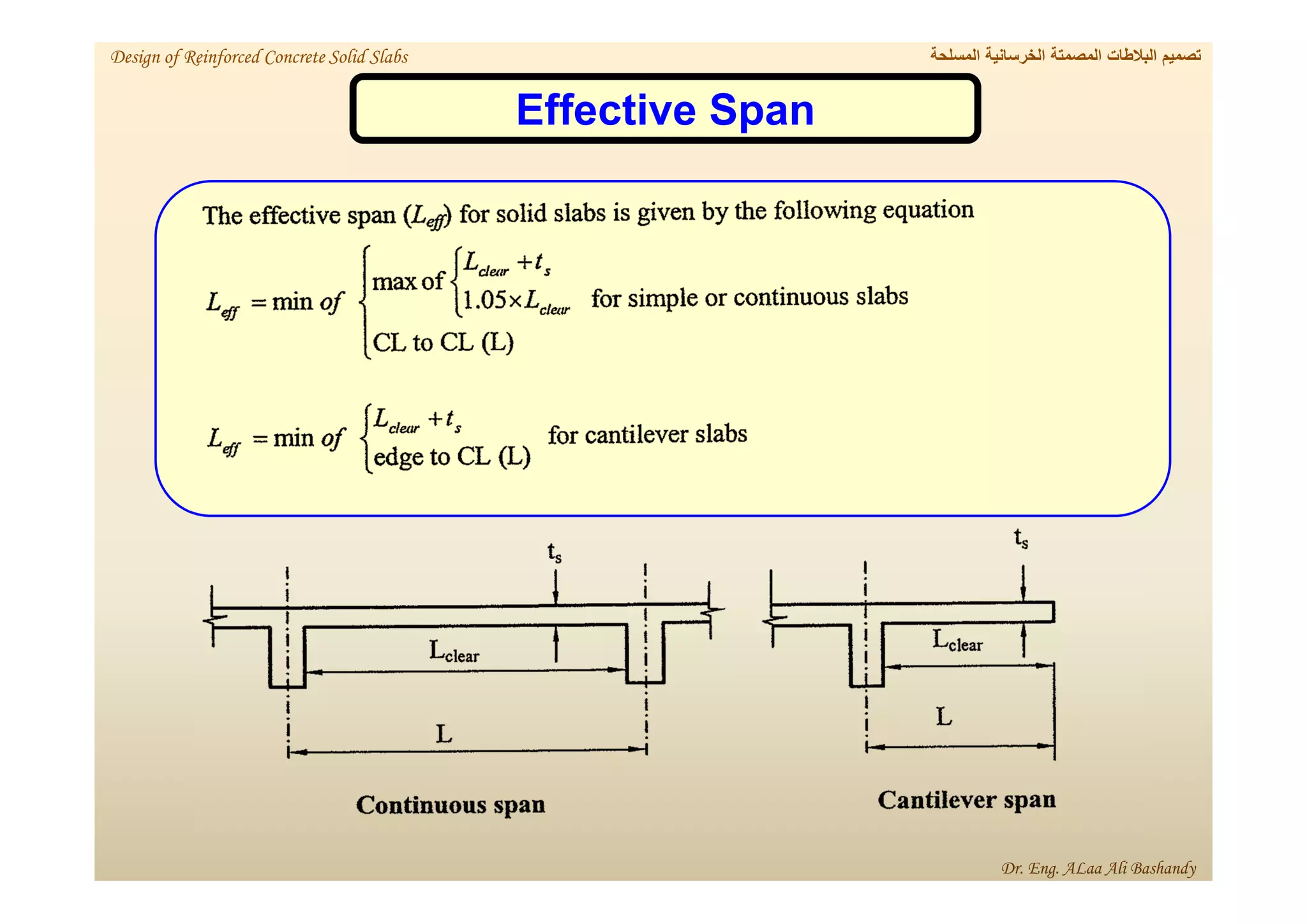
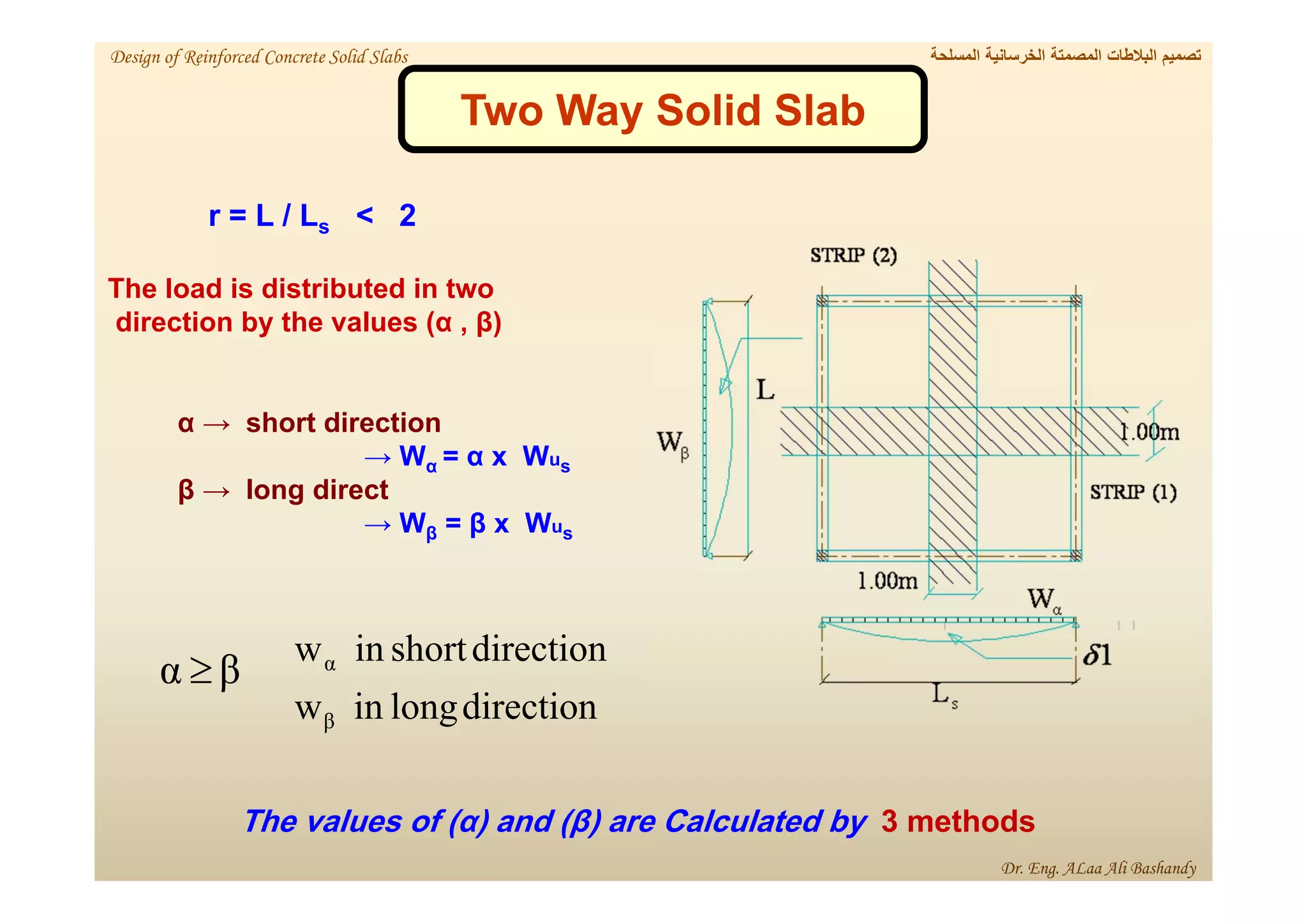
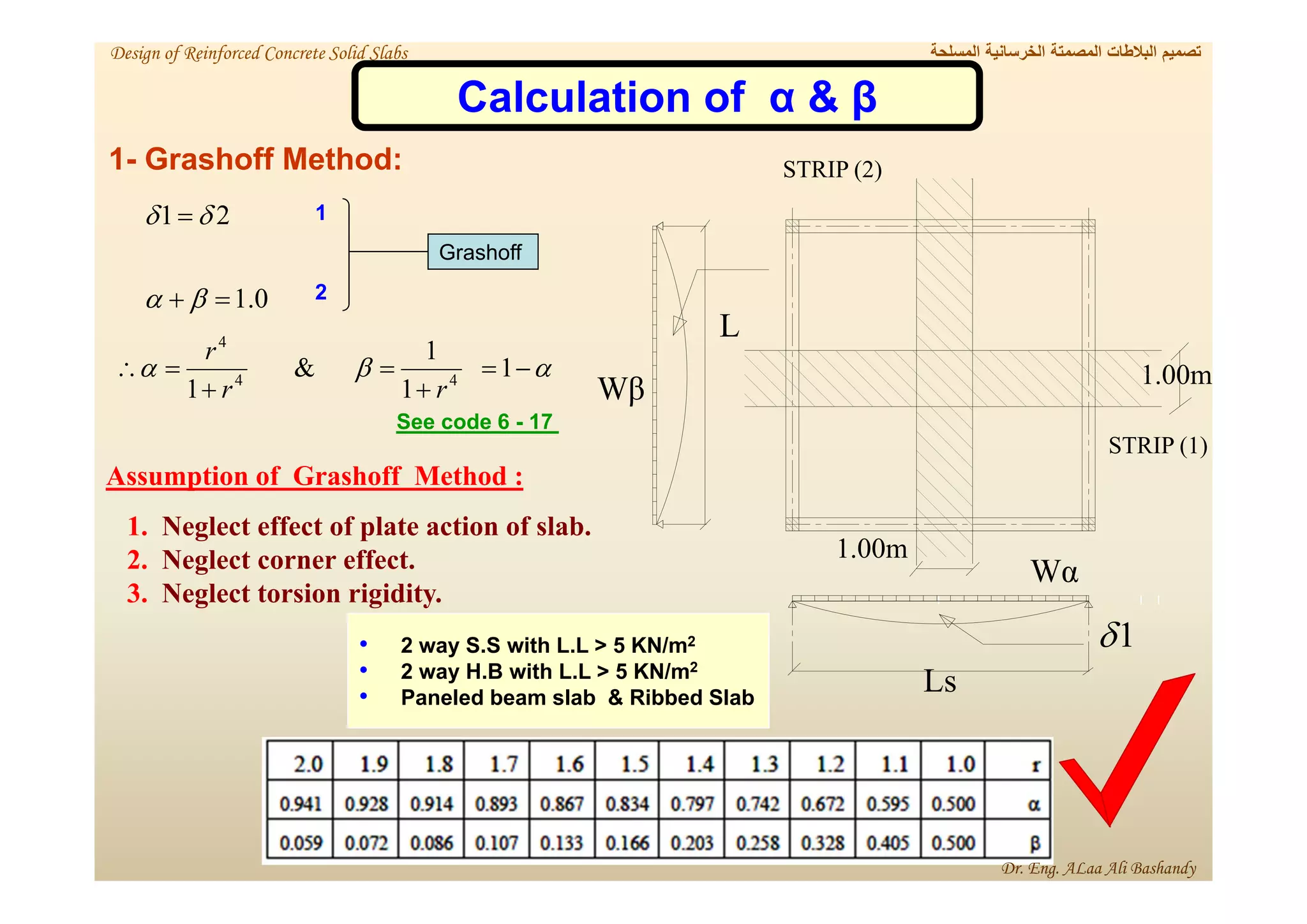
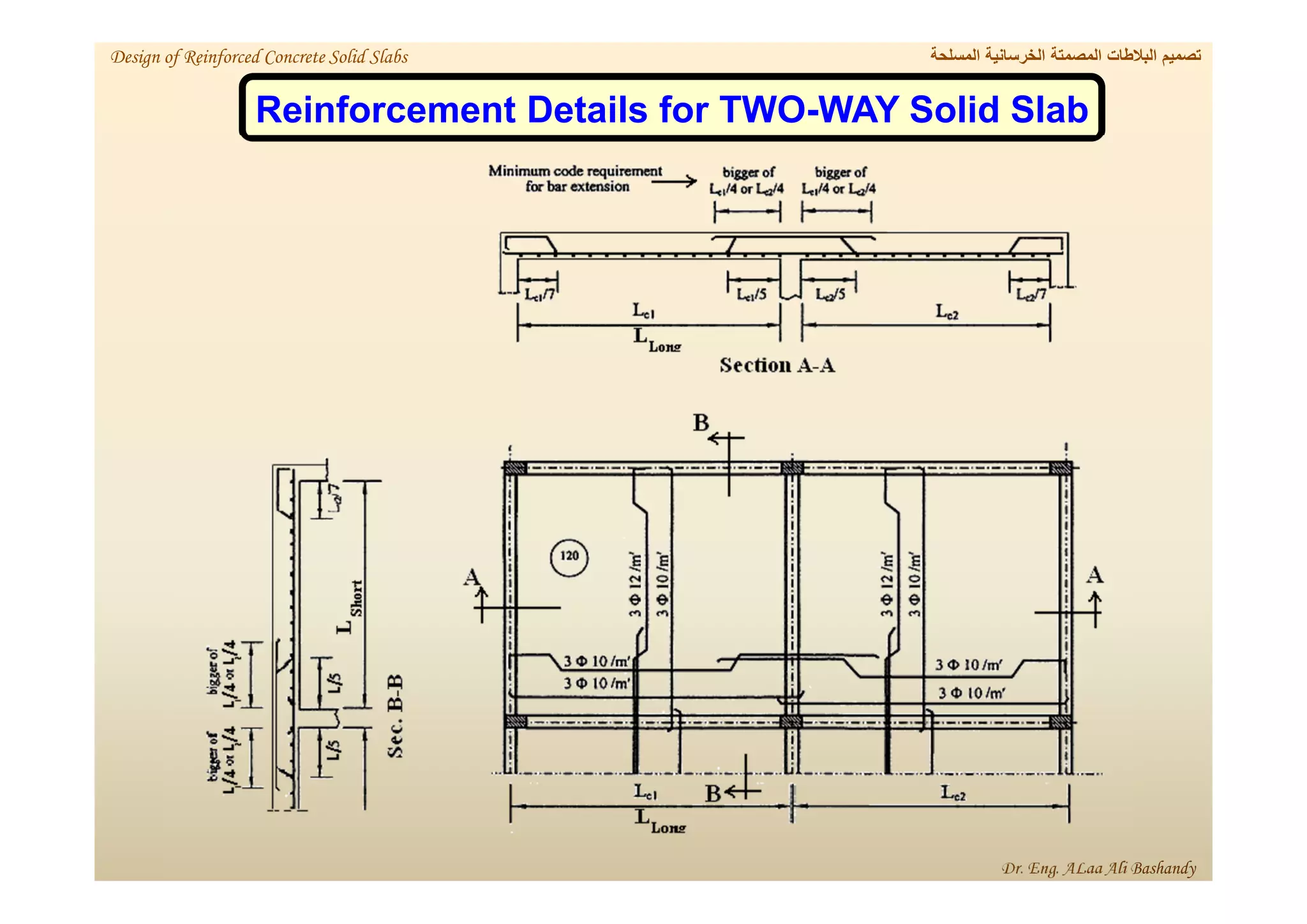
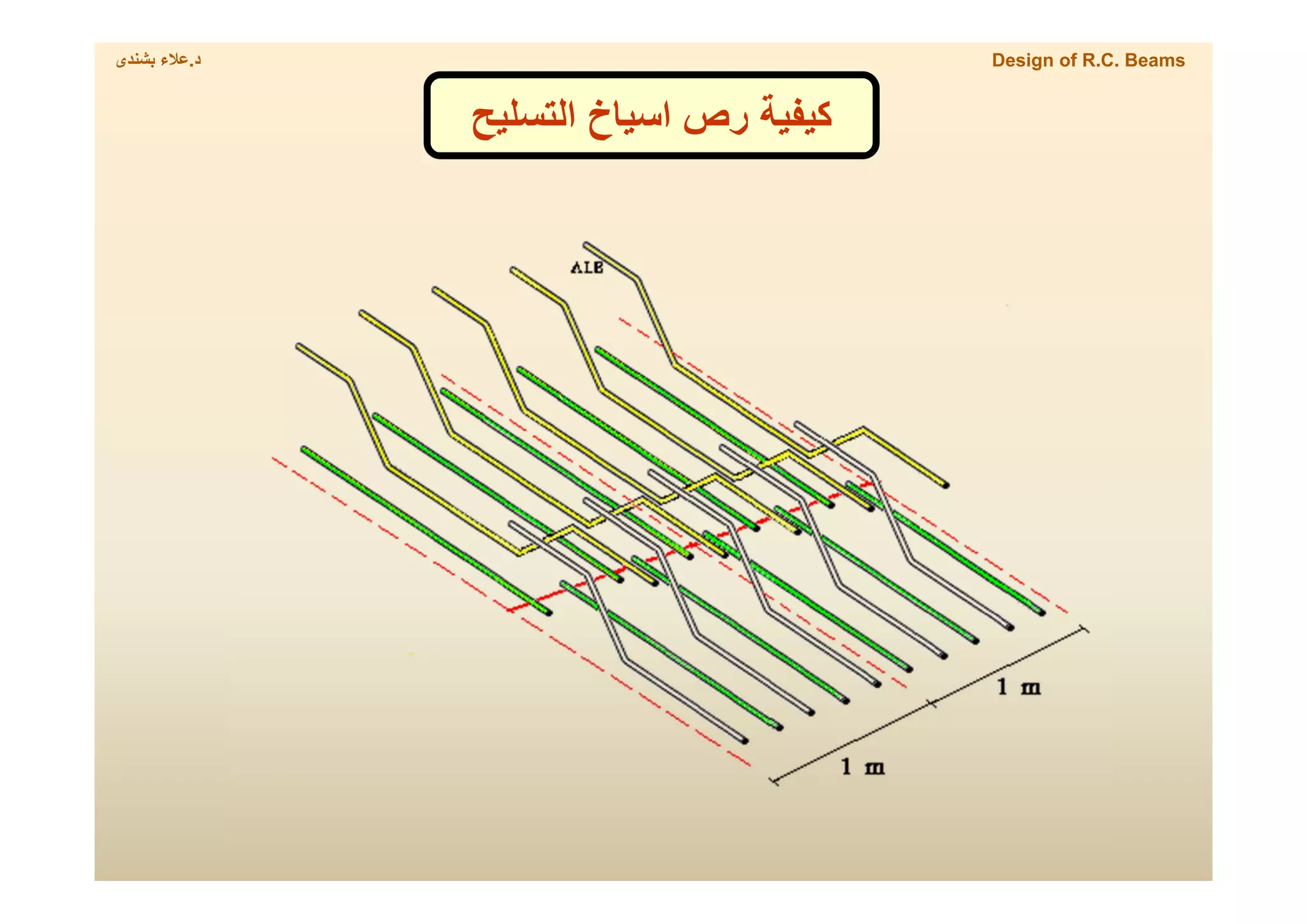
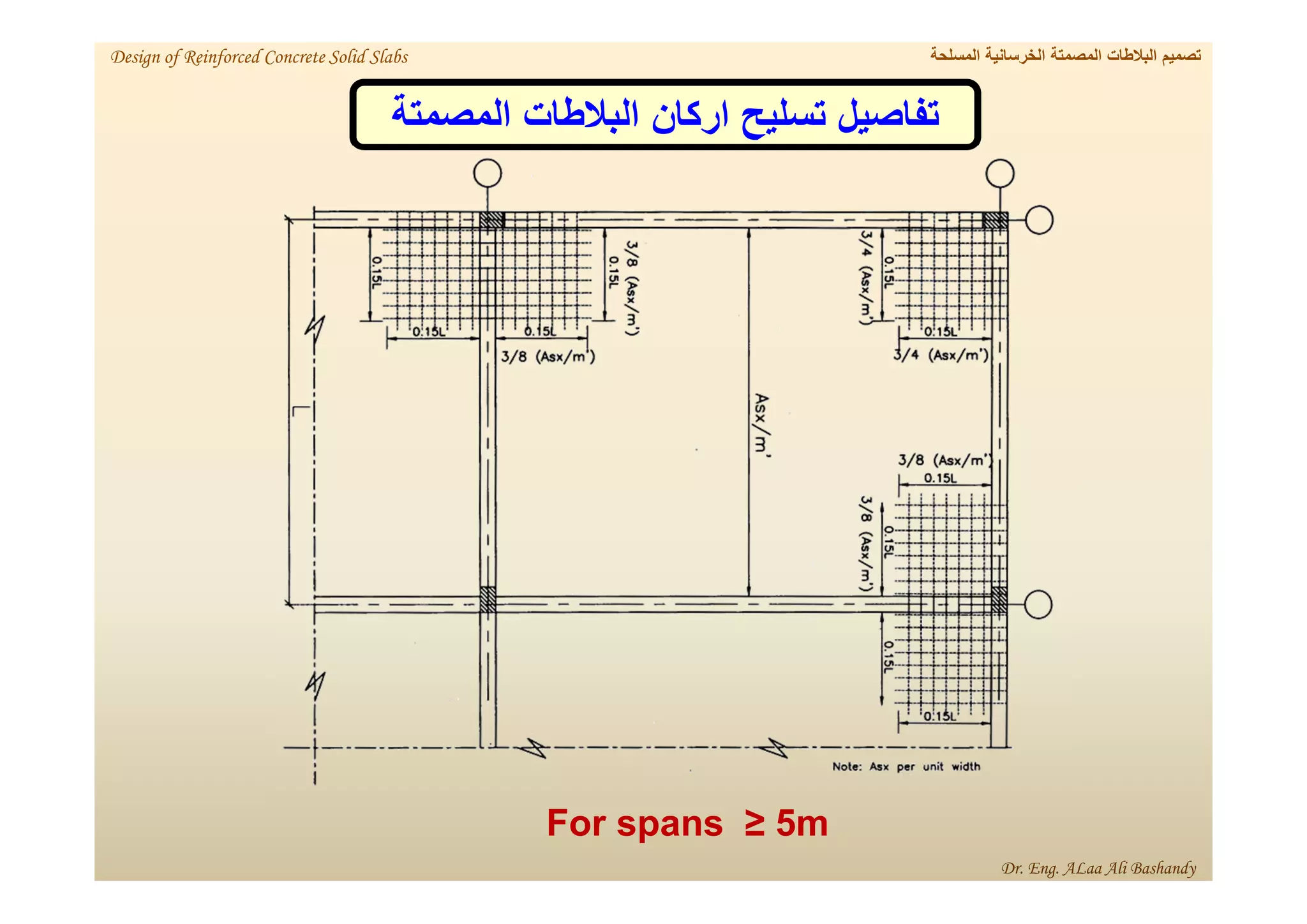
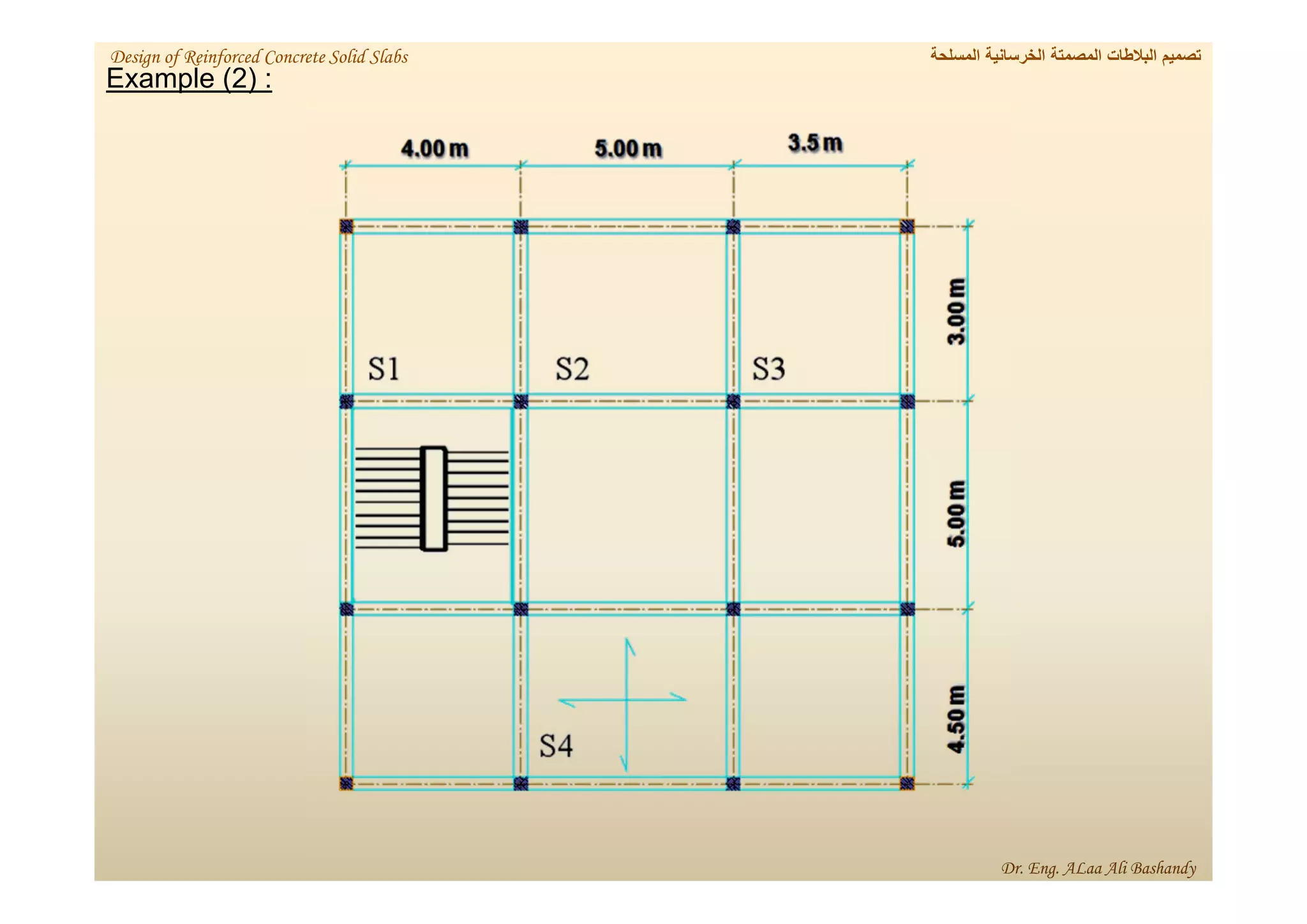
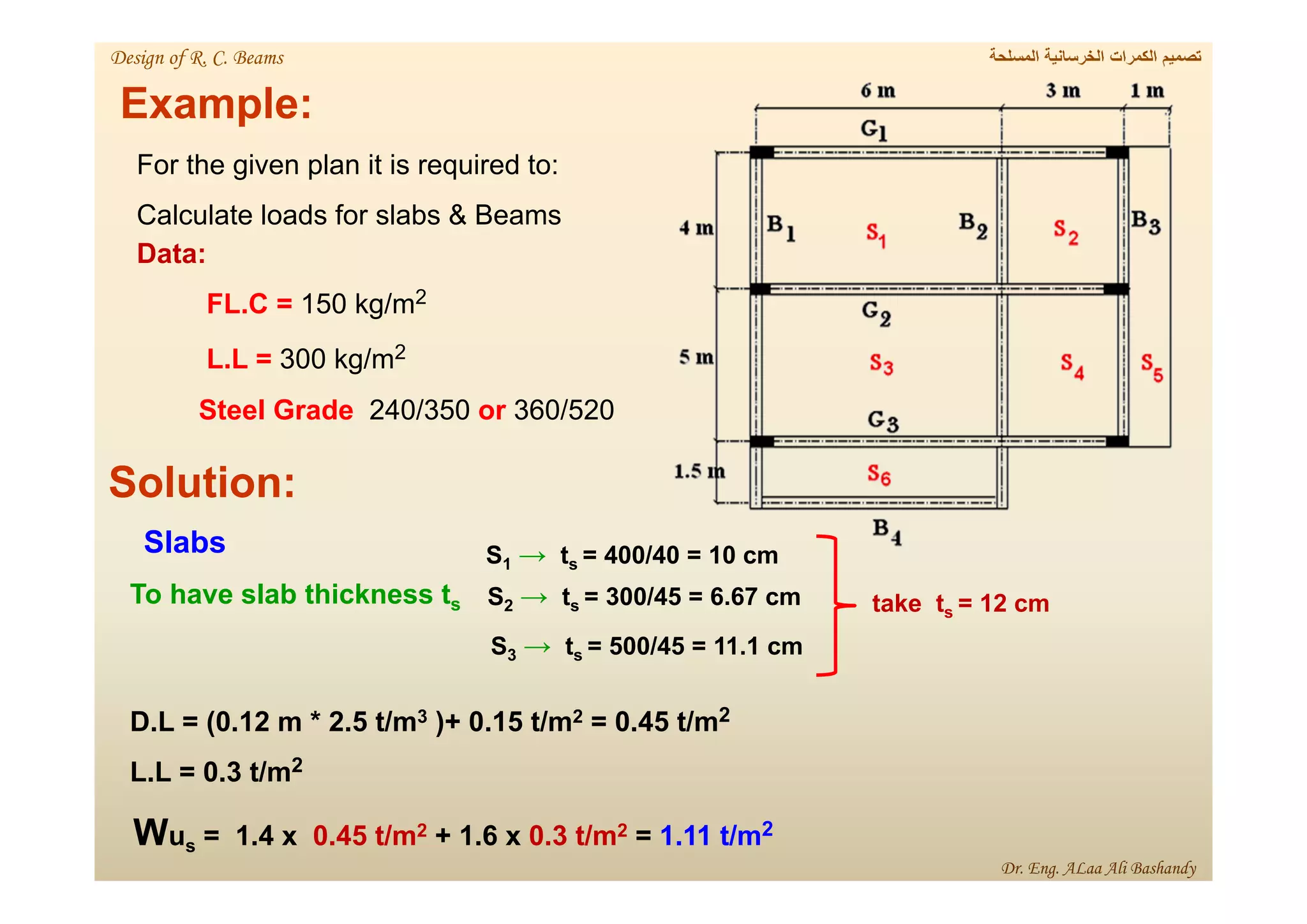
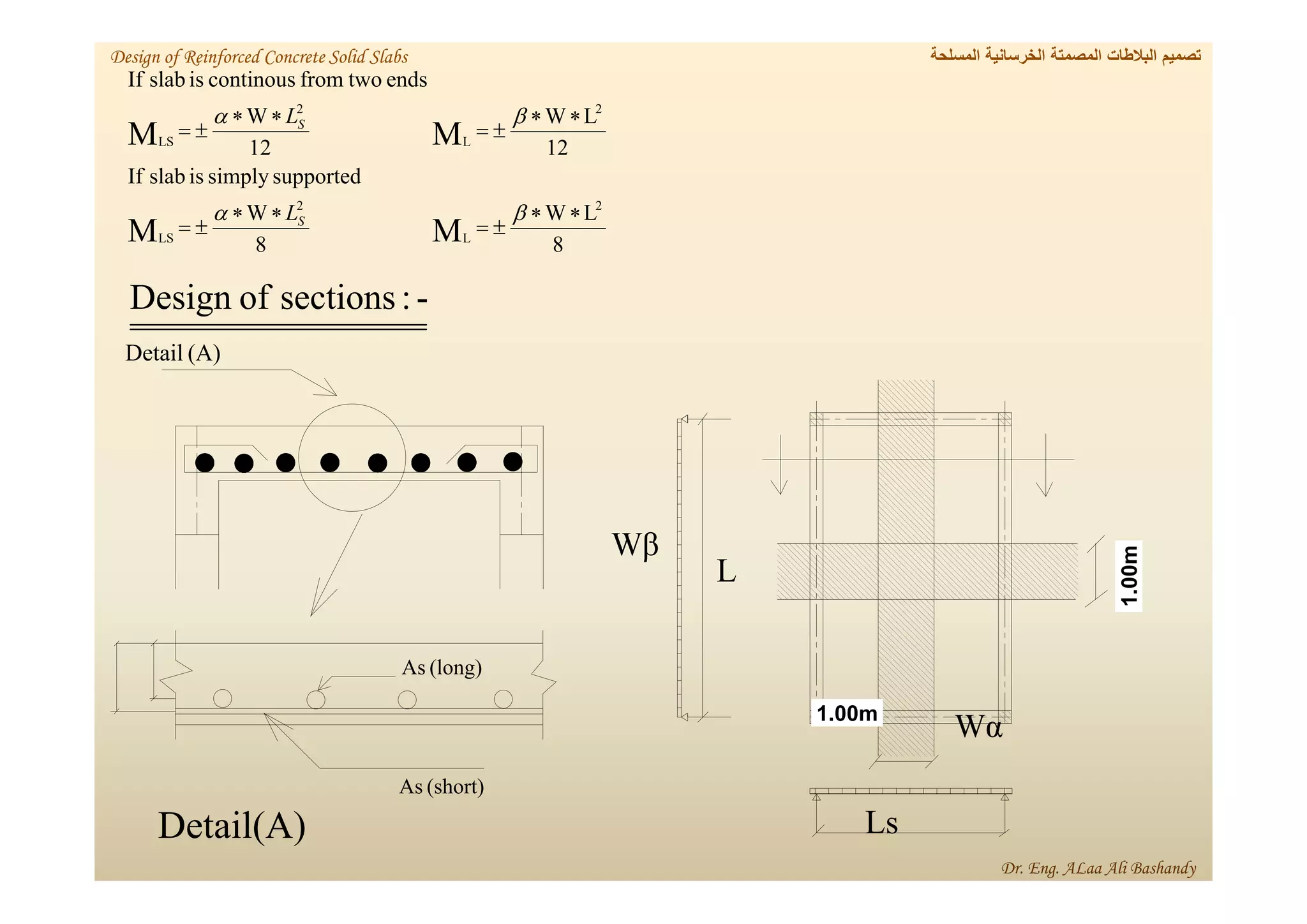
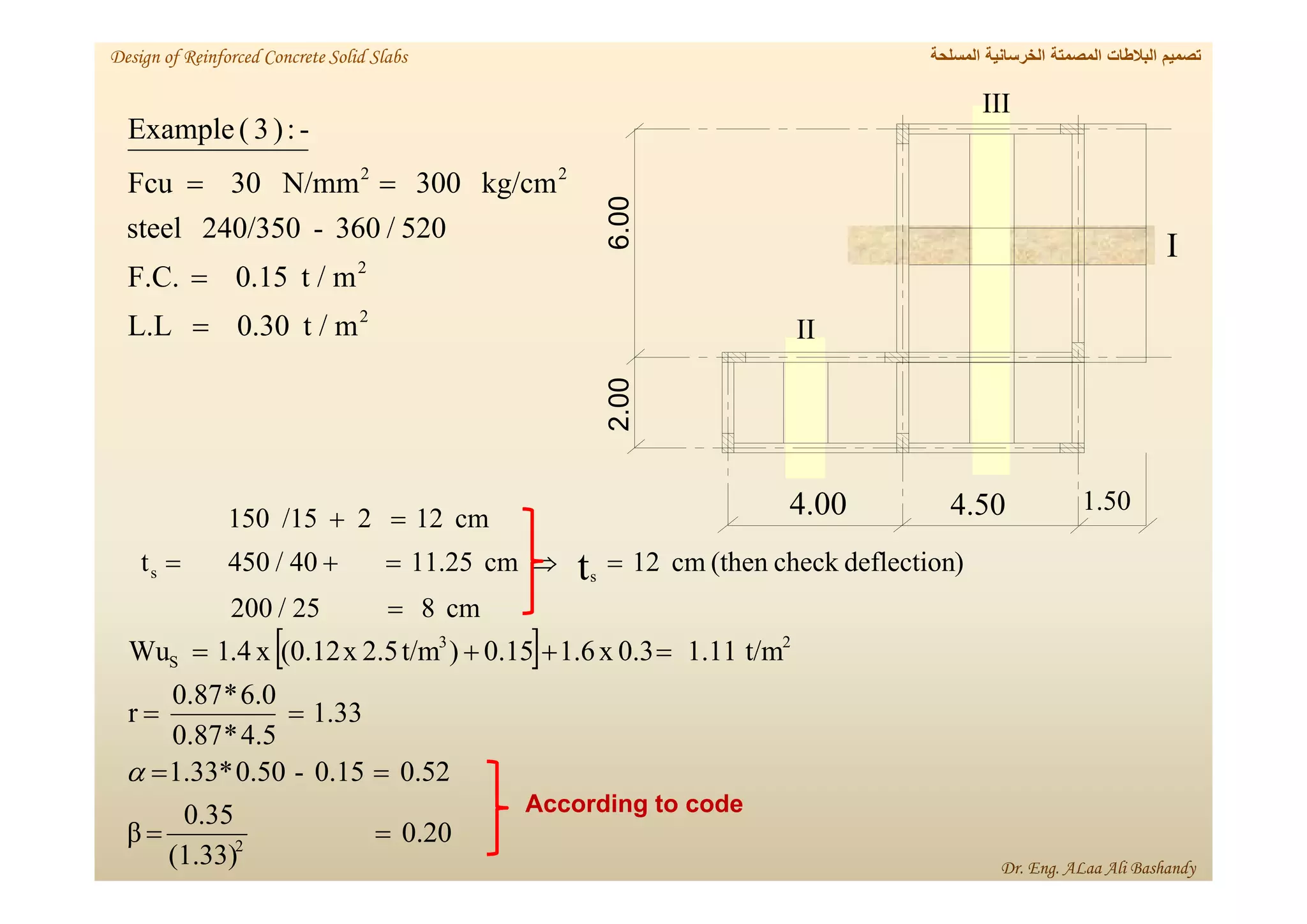
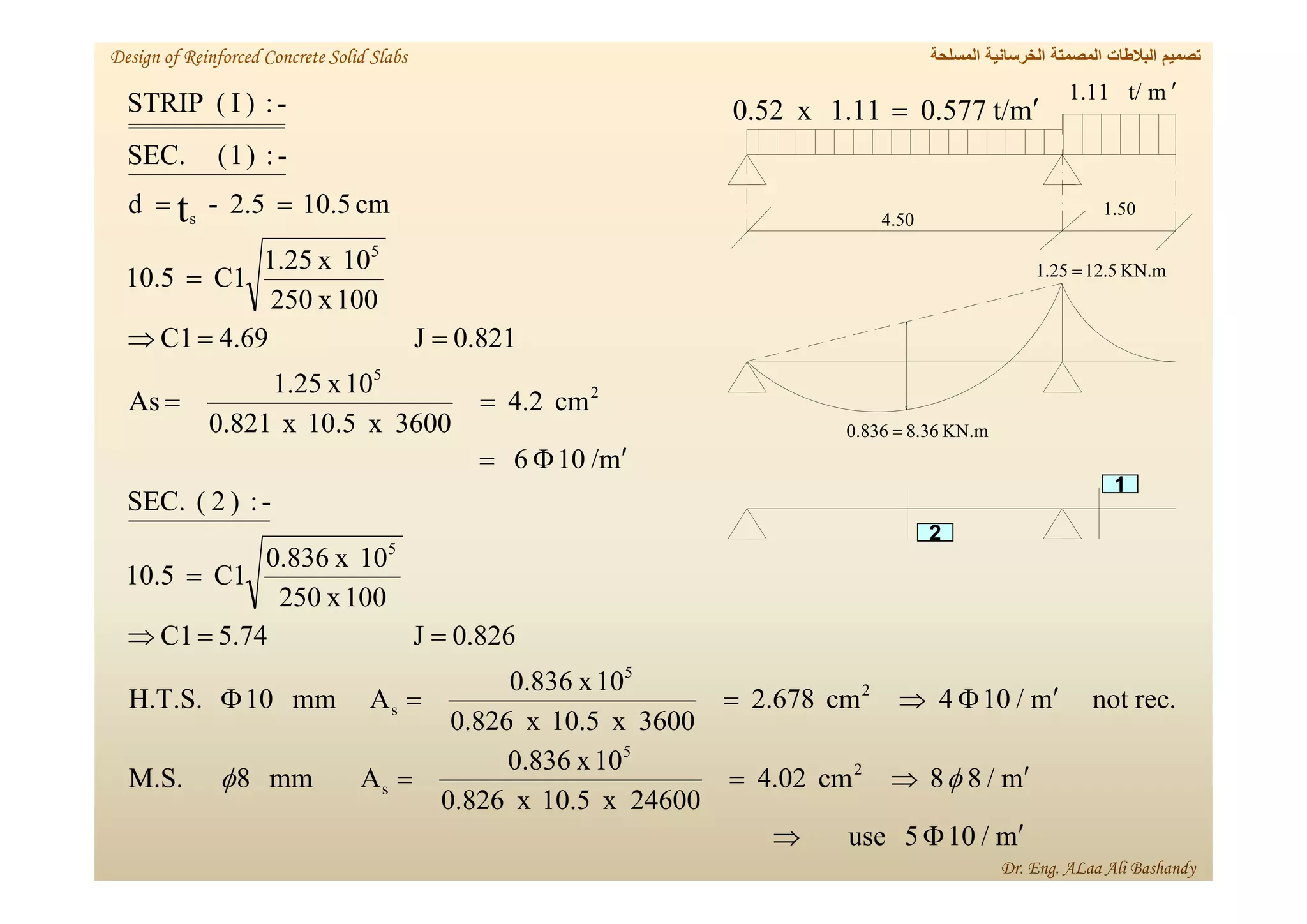
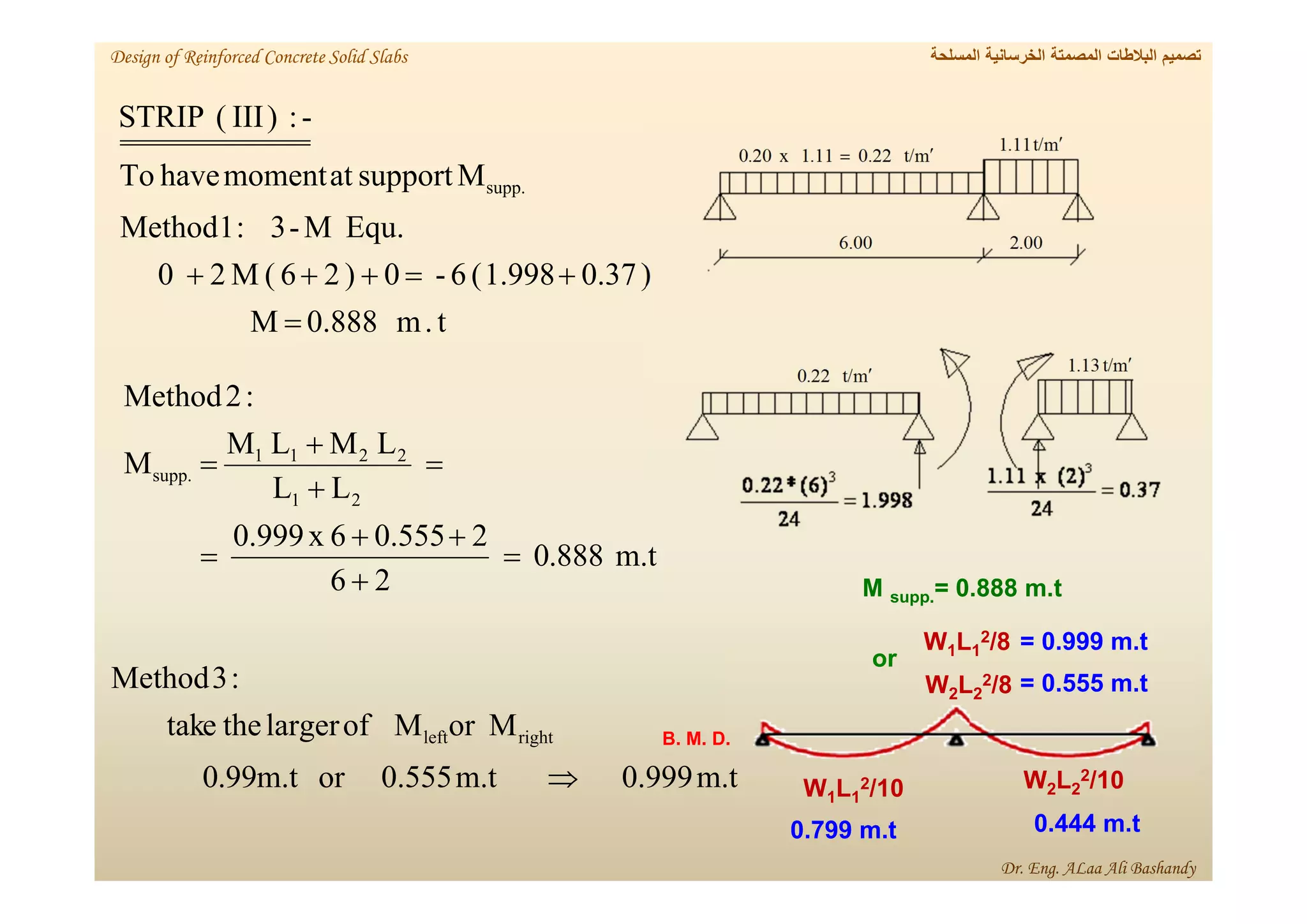
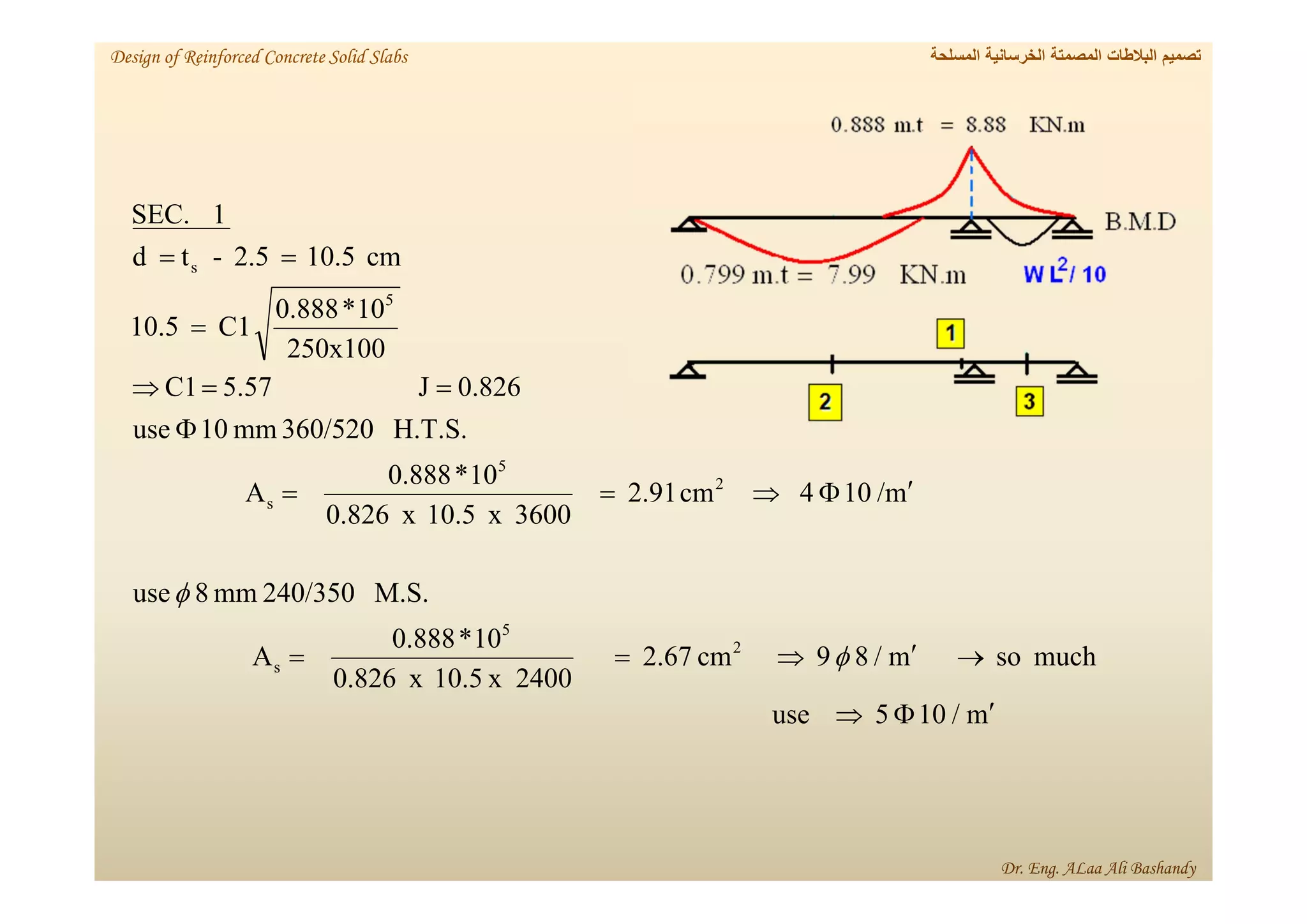
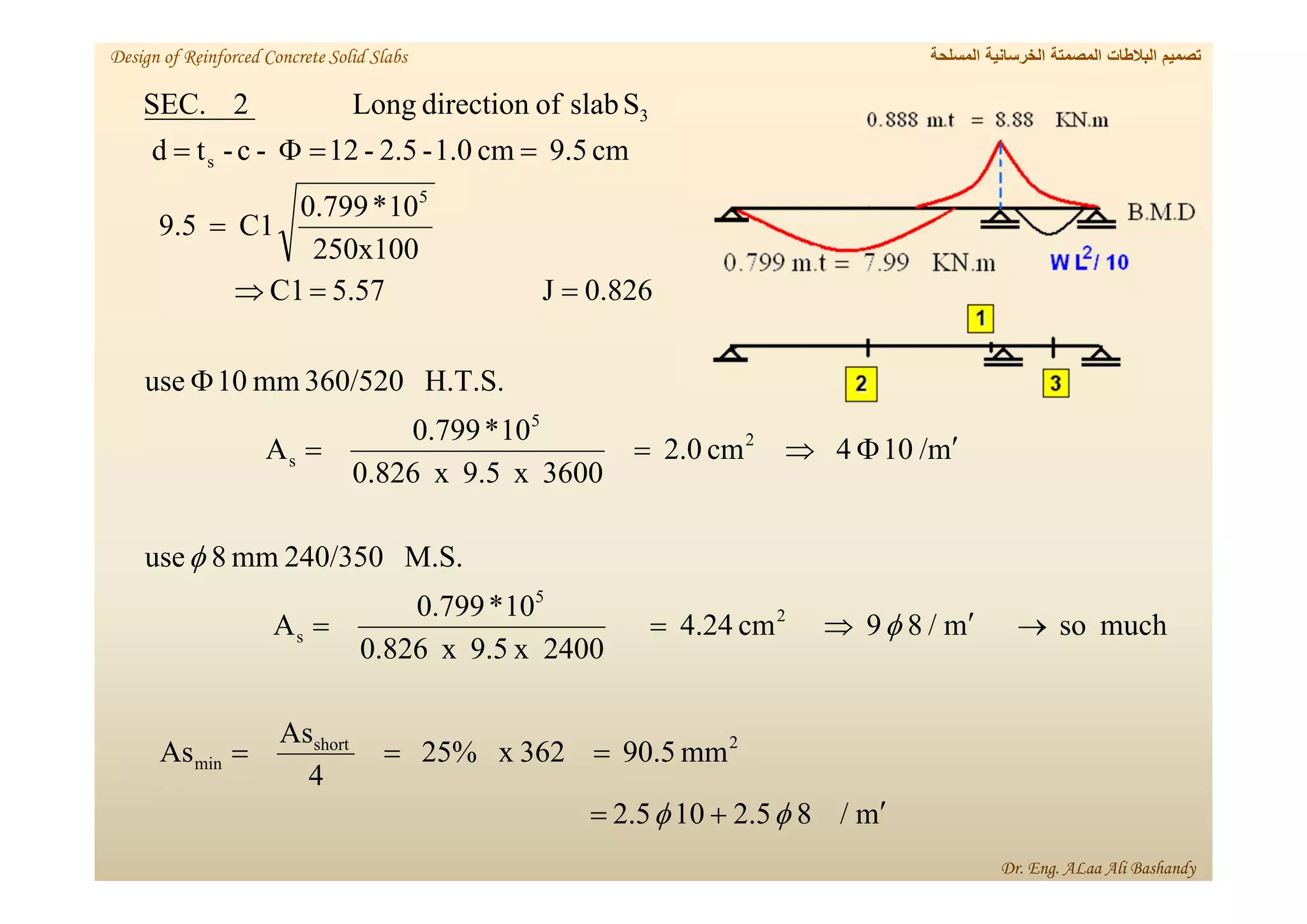
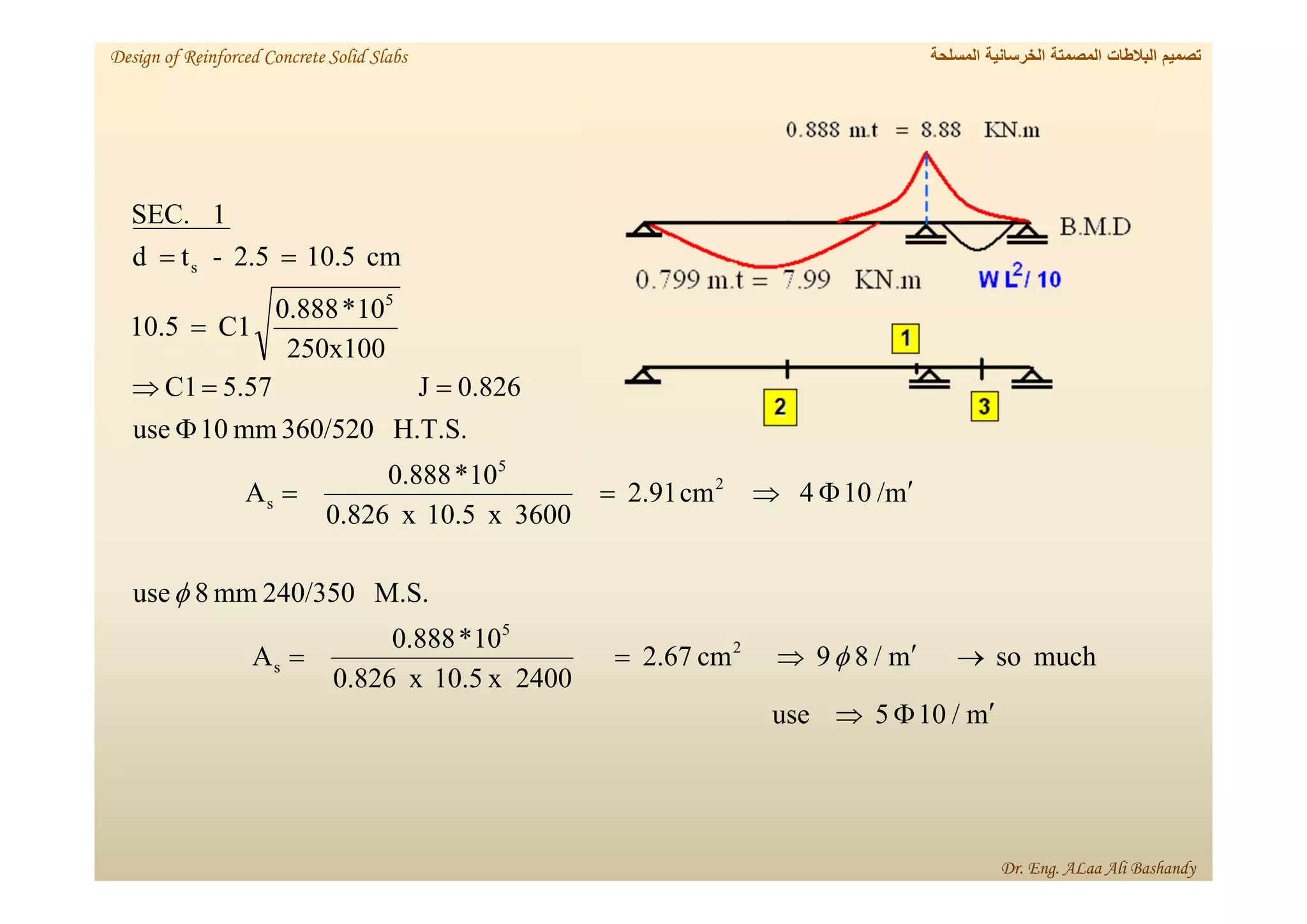
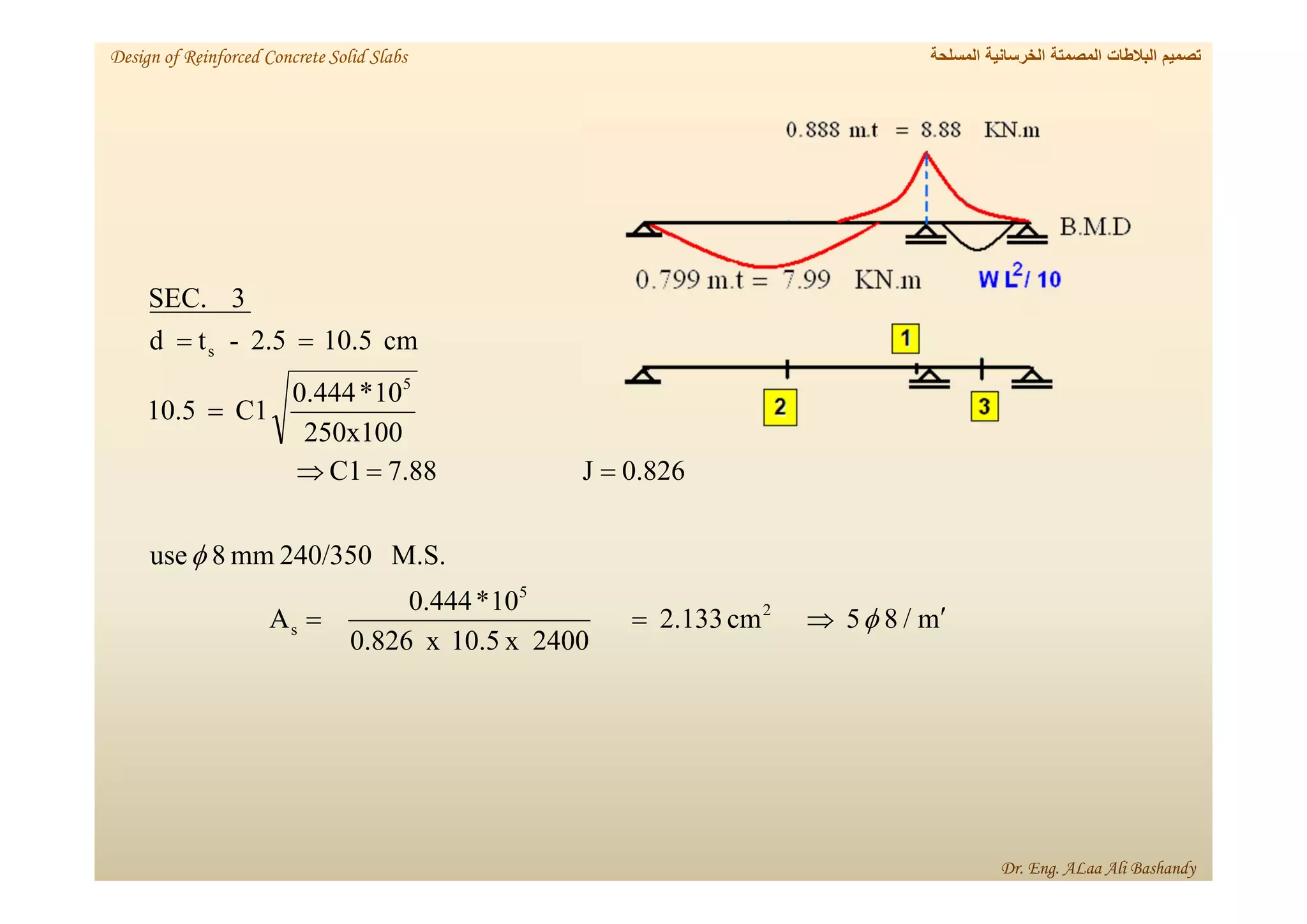
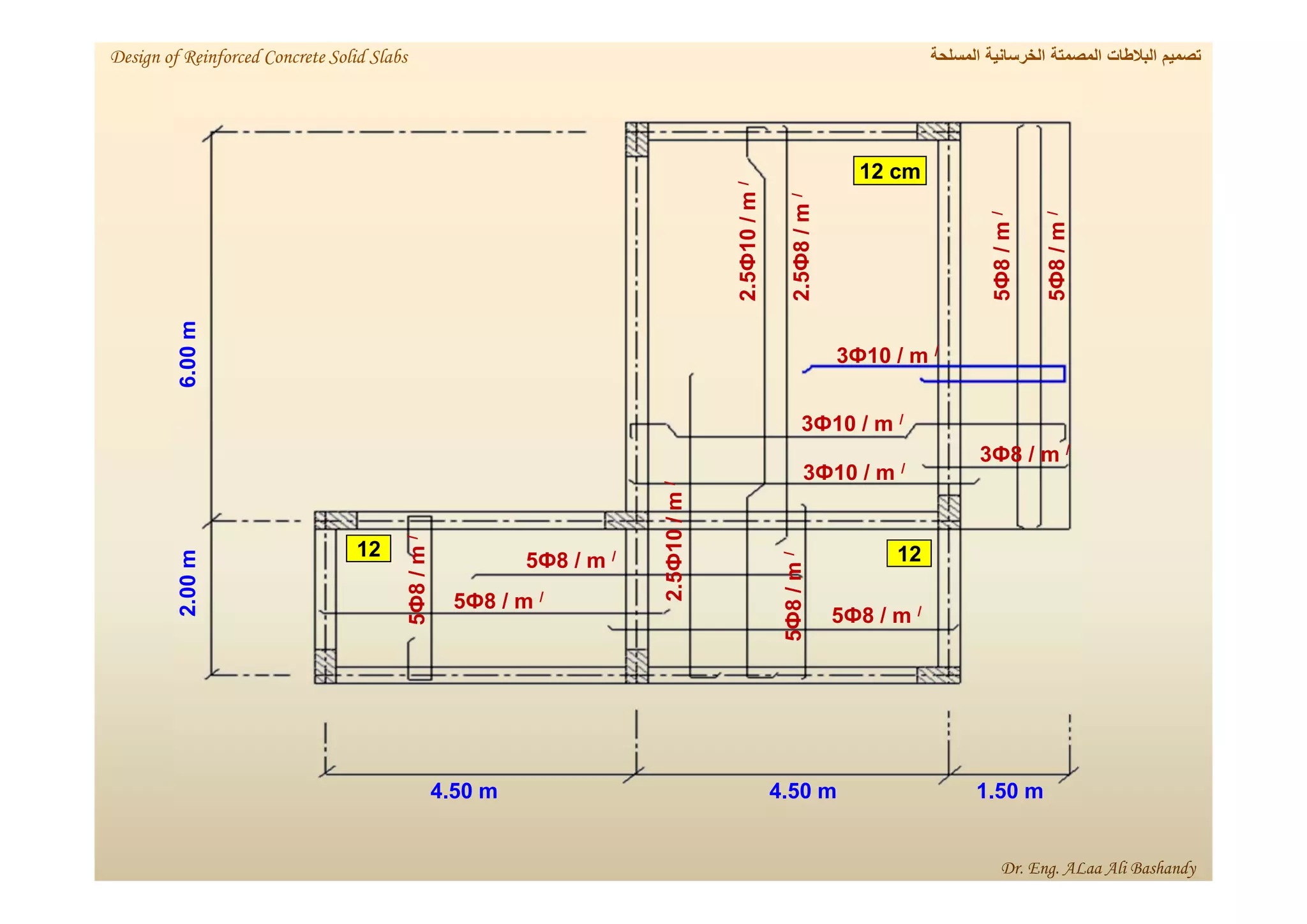
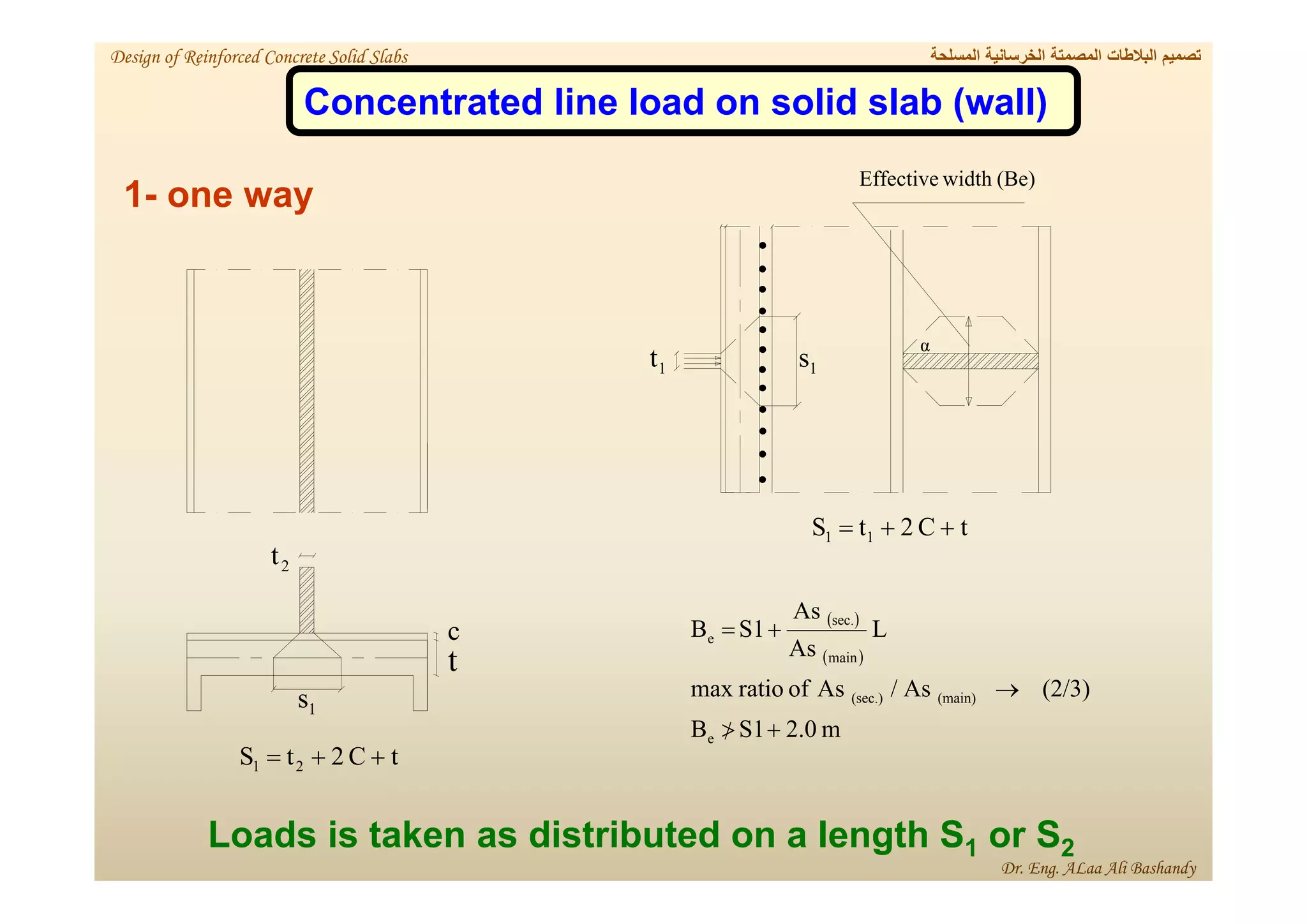
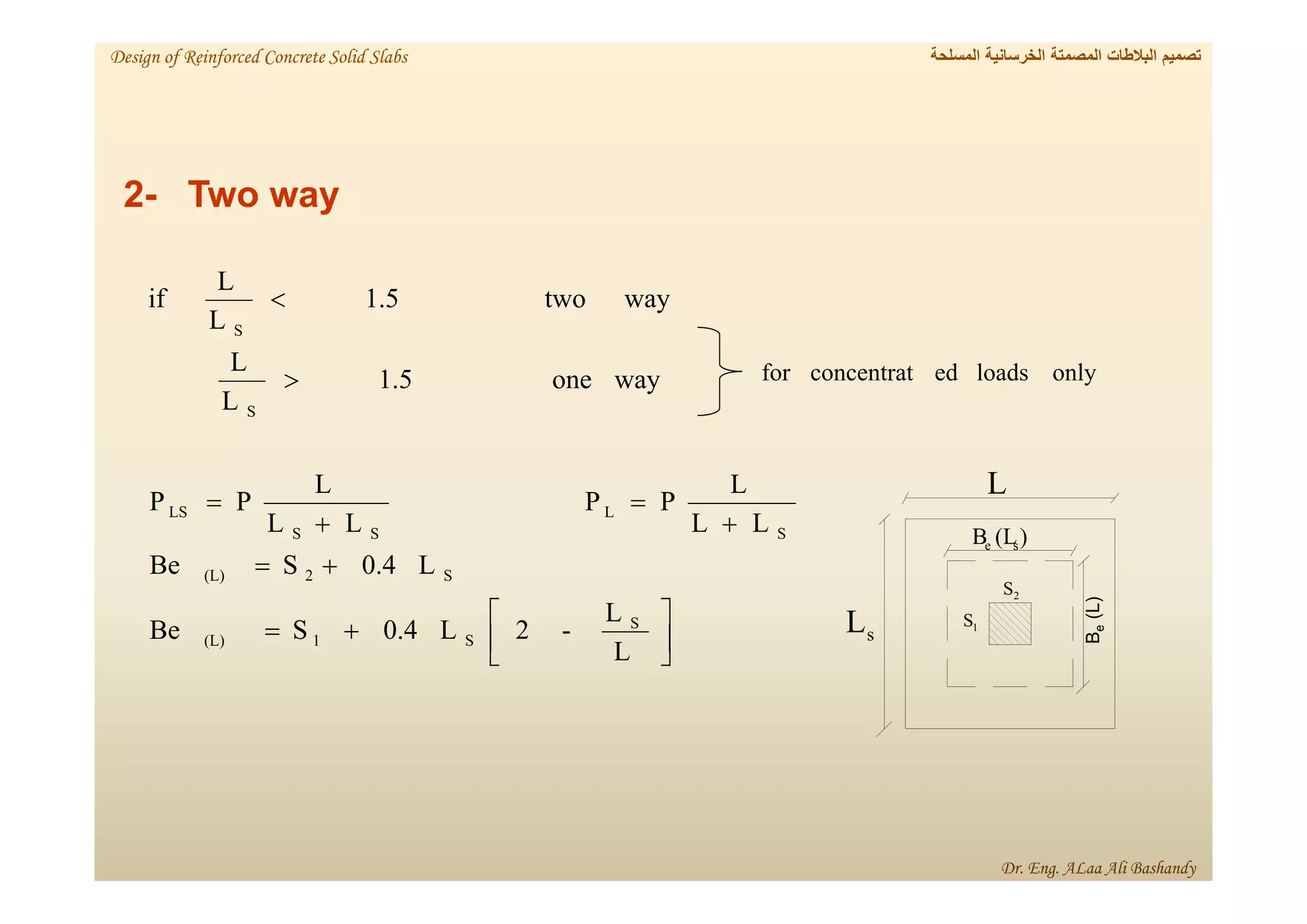
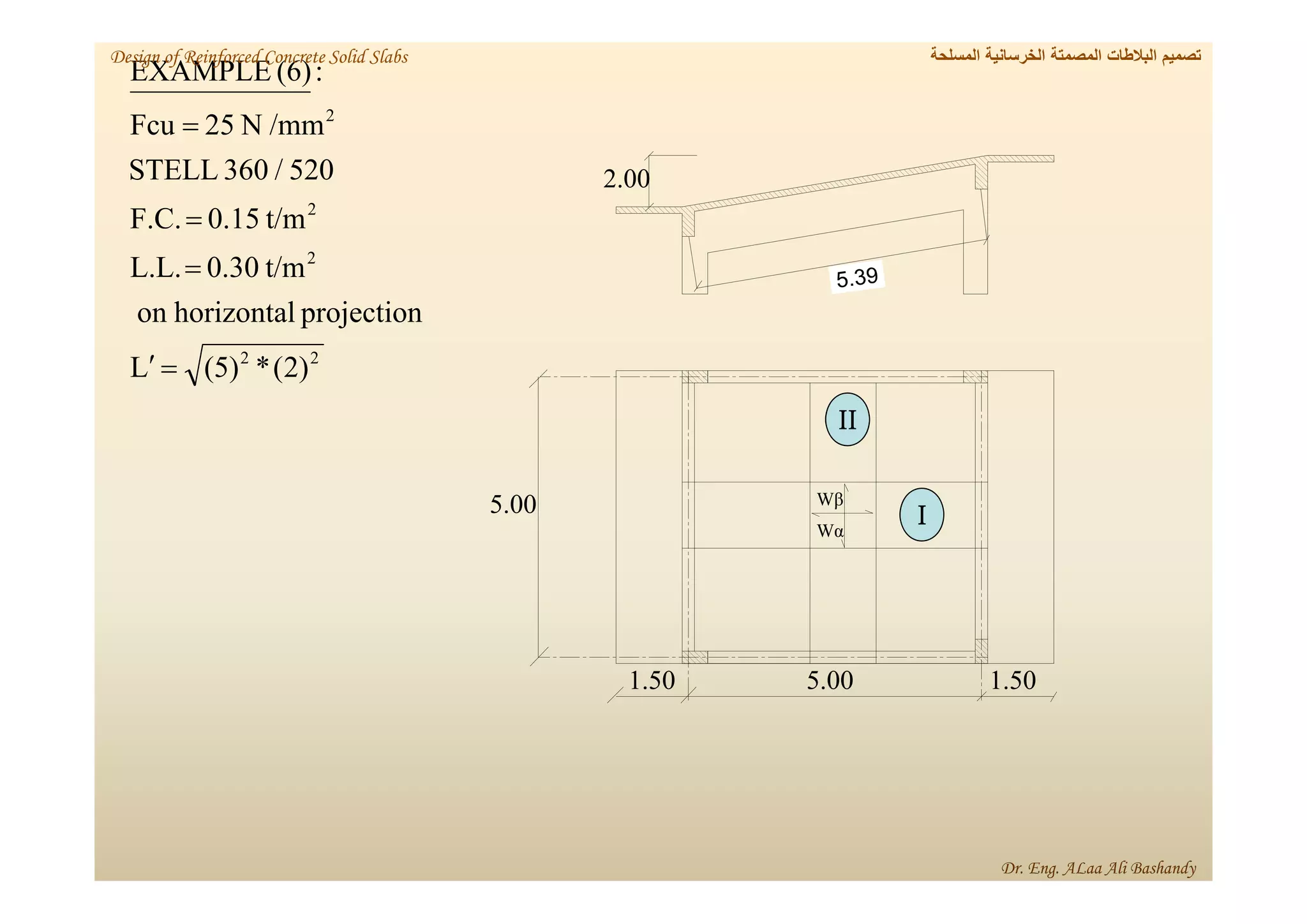
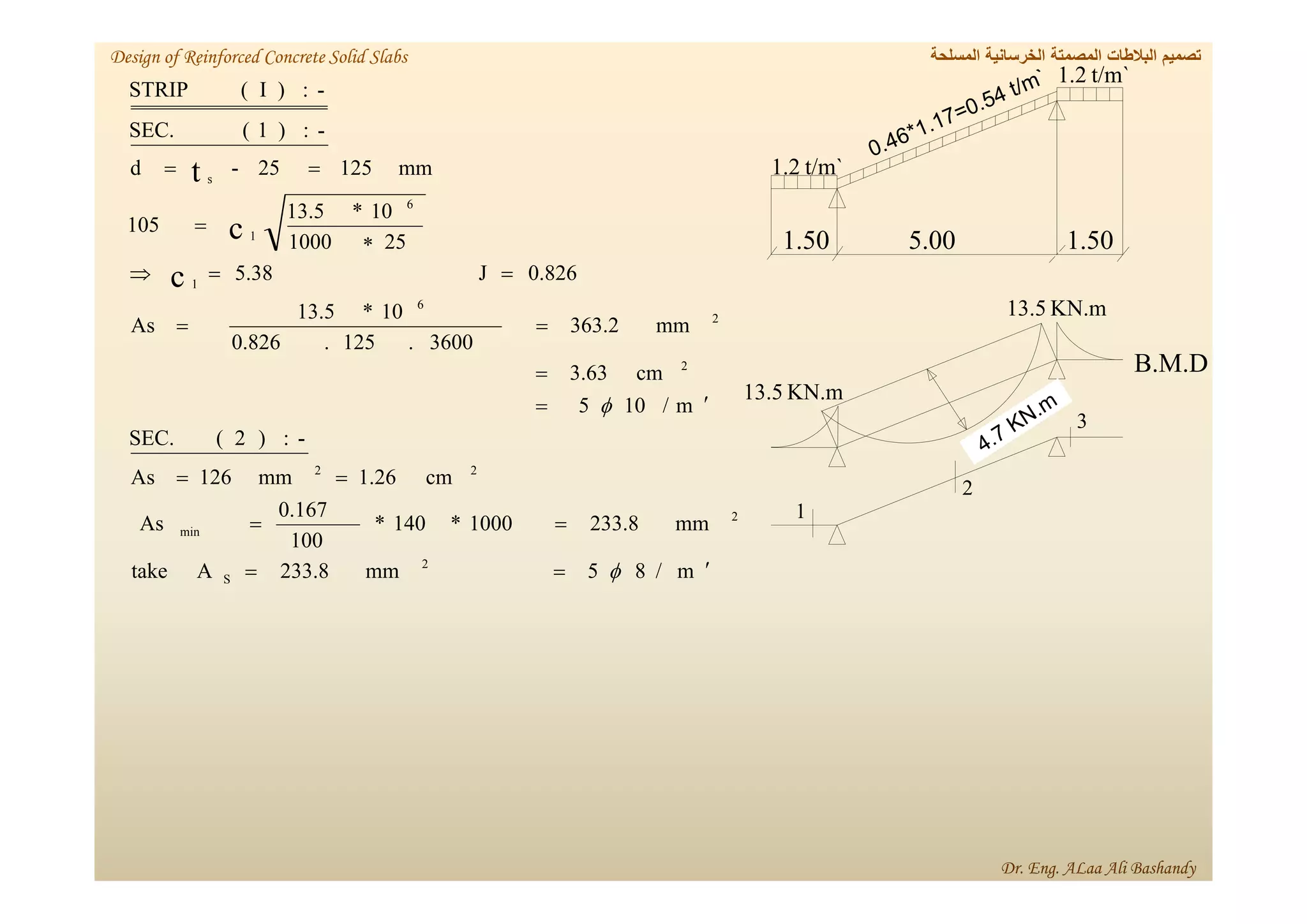
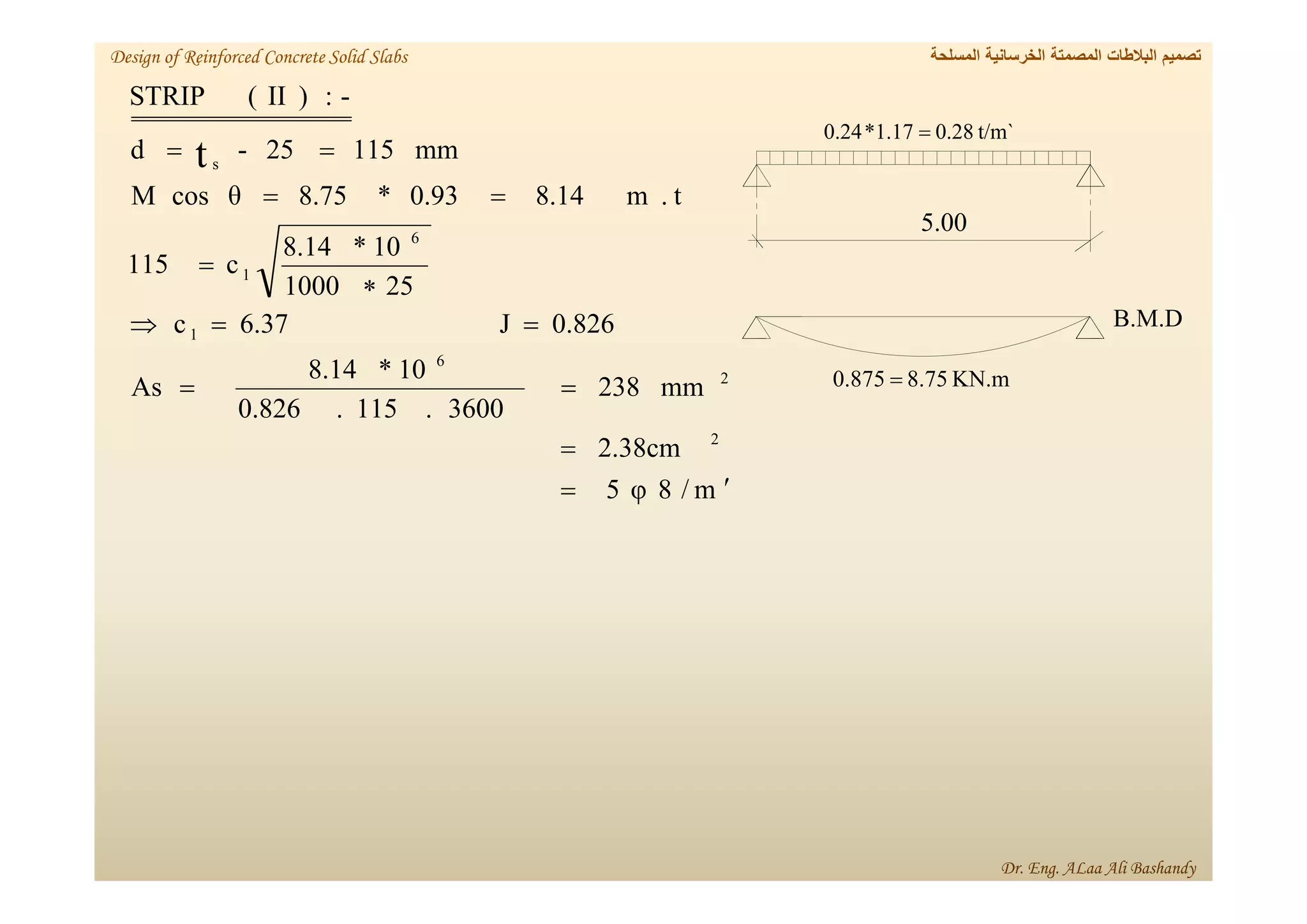
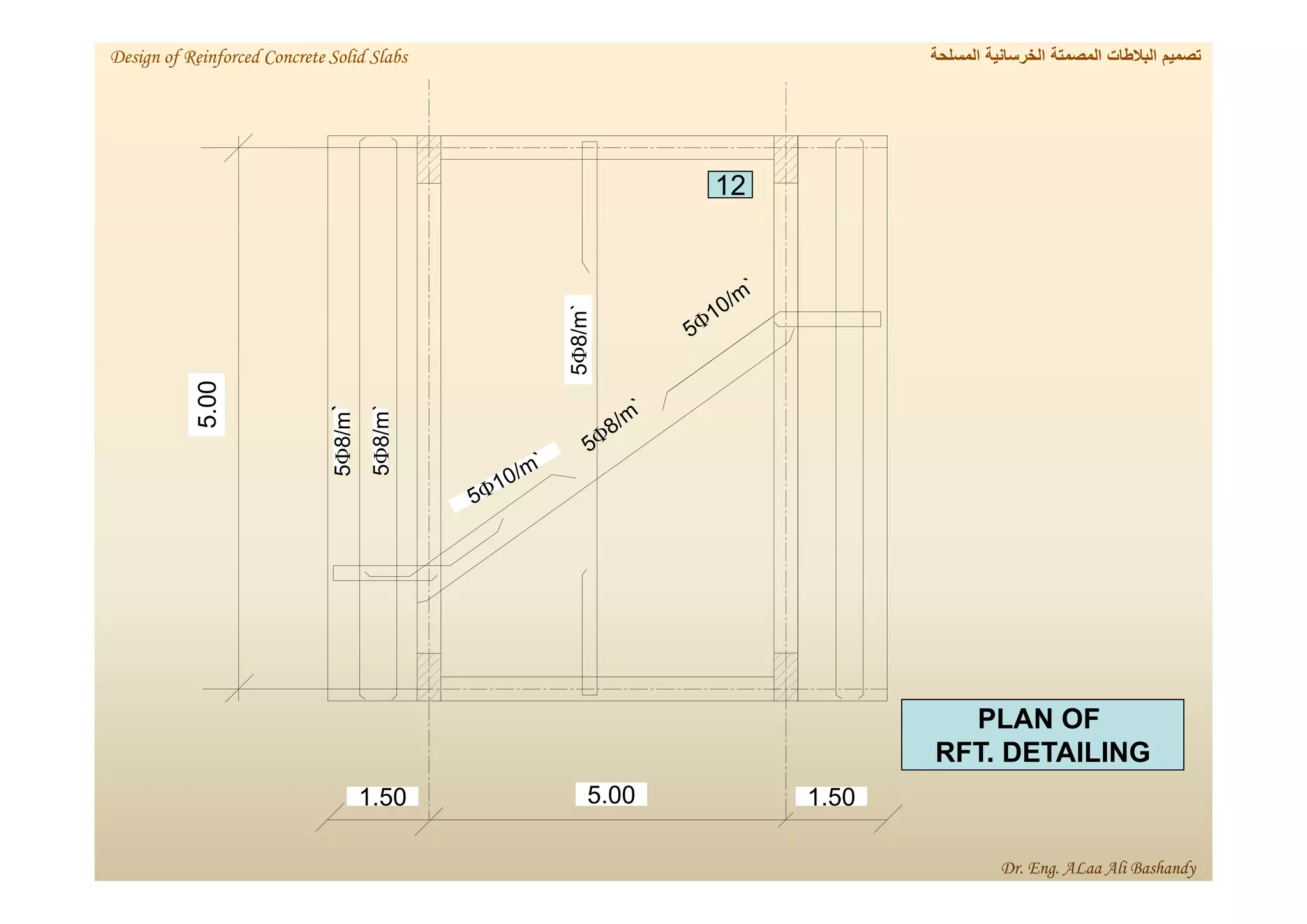
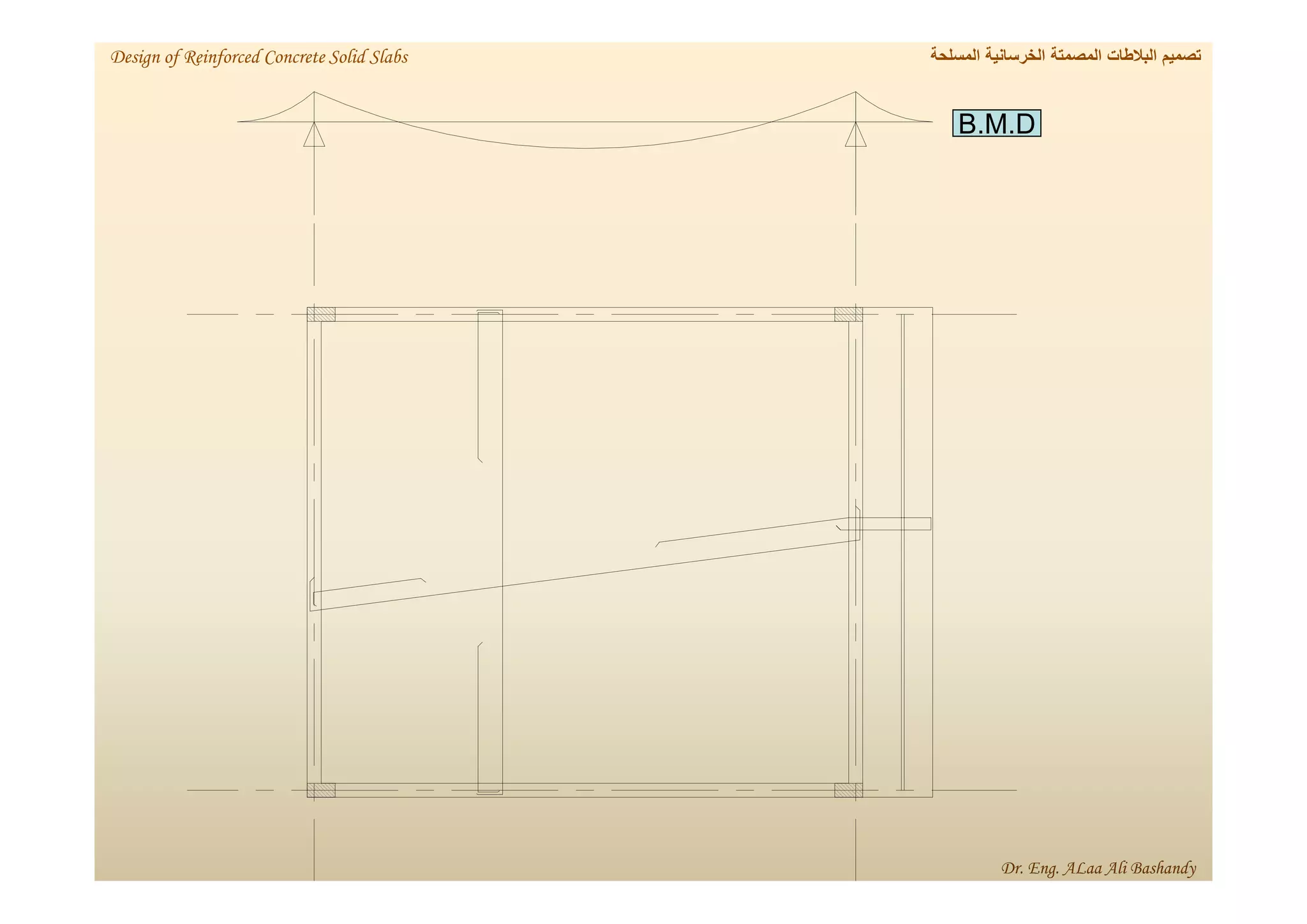
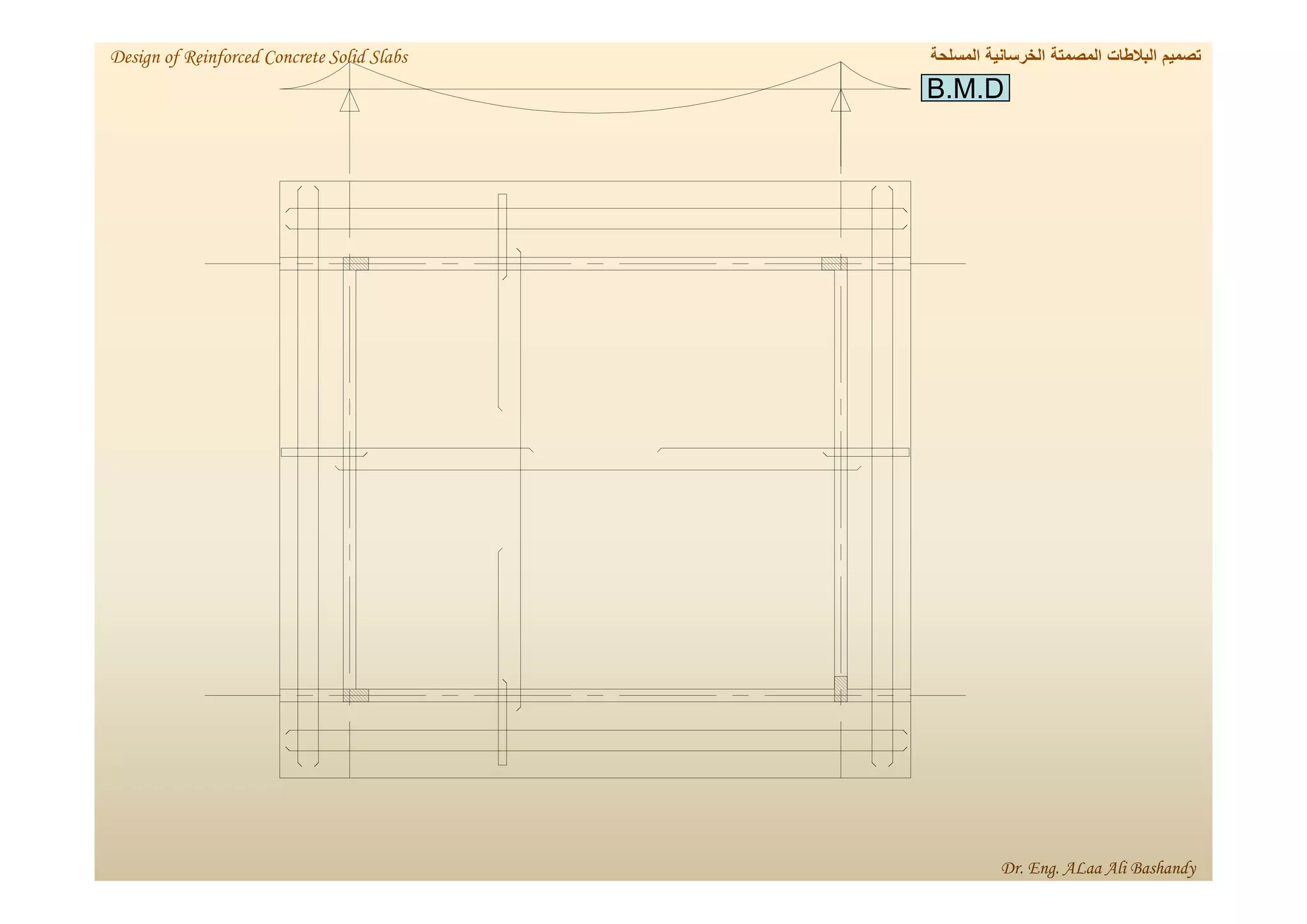
This document provides a summary of the design of reinforced concrete solid slabs. It begins with an introduction and outlines the topics to be covered, including the types of concrete slabs, how to calculate slab loads, and the design process for solid slabs involving concept, preliminary dimensions, load calculation, section sizing, reinforcement calculation, and drawing details. Key points covered are one-way and two-way solid slabs, minimum slab thickness, reinforcement ratios and spacing, and guidelines for slab thickness estimation based on span length and load type.