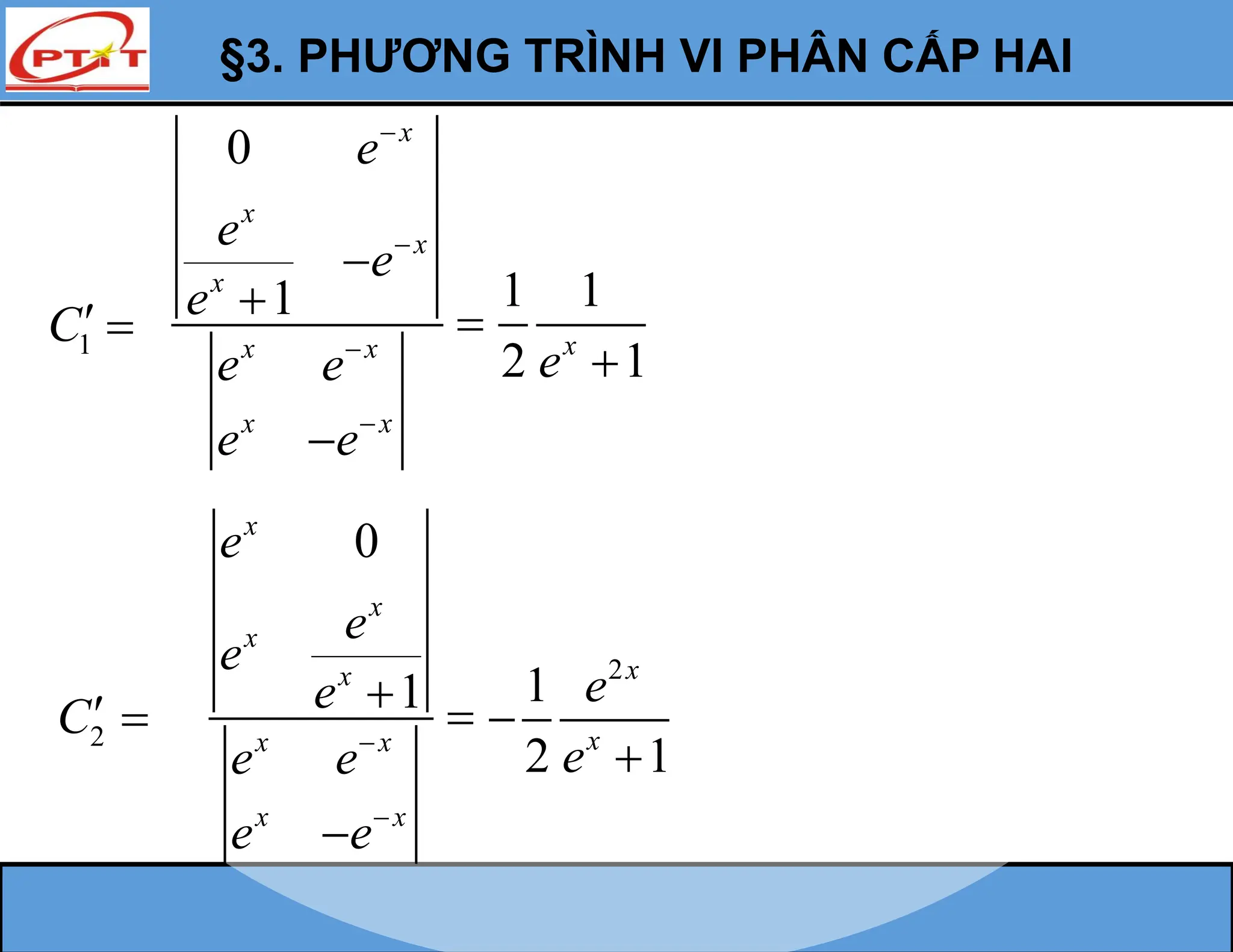
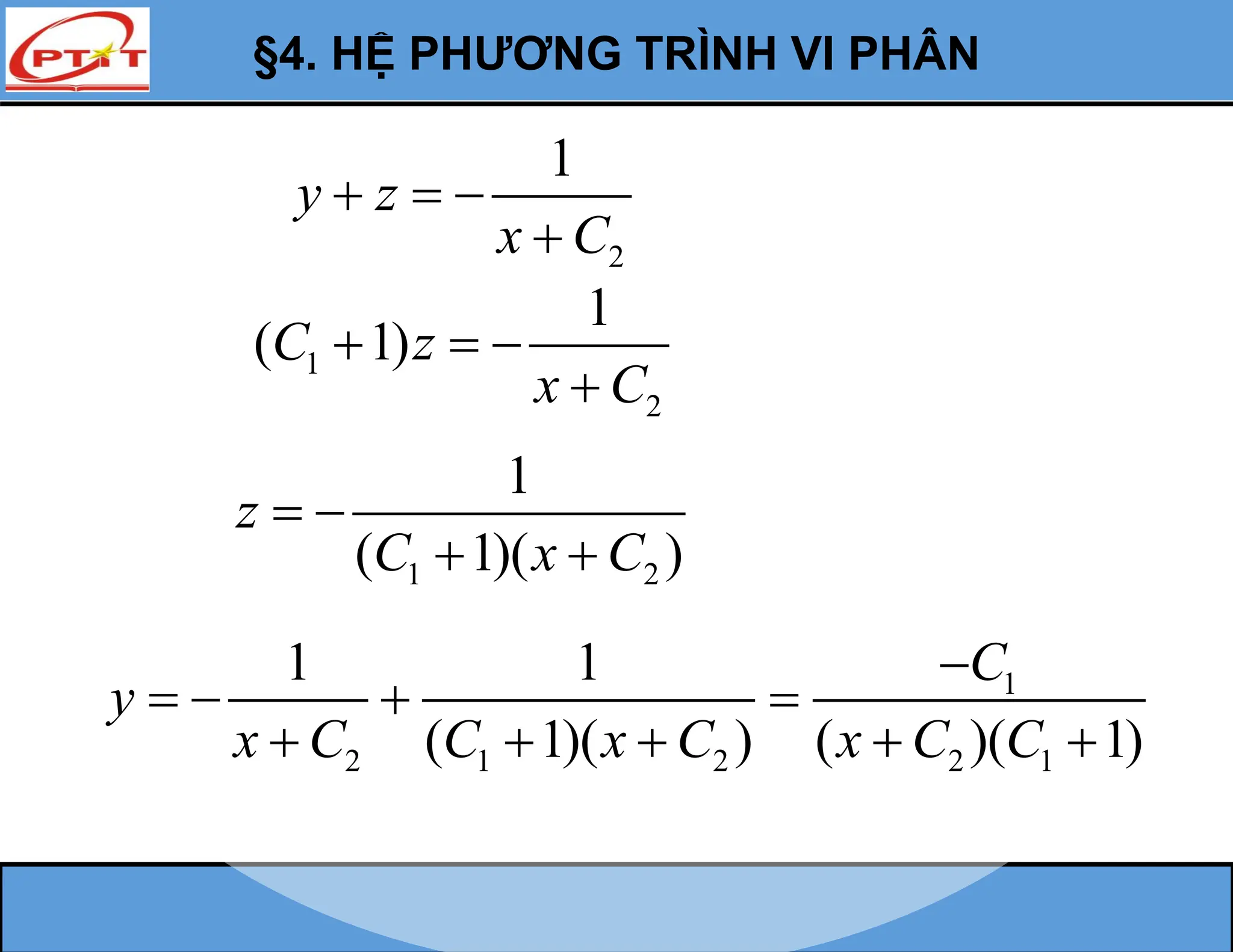
Chương 4 trình bày về phương trình vi phân, định nghĩa và phân loại như phương trình tuyến tính, cấp một, và các phương trình đặc biệt như phương trình đẳng cấp. Tài liệu cung cấp các công thức giải và ví dụ minh họa cho từng loại phương trình, đồng thời nhấn mạnh sự tồn tại và tính duy nhất của nghiệm. Nội dung cũng đề cập đến các nghiệm tổng quát, riêng và kì dị của các phương trình vi phân.