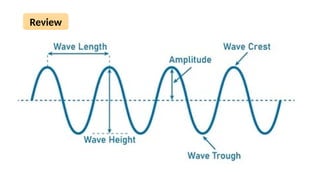
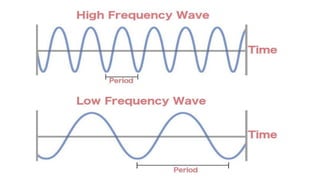
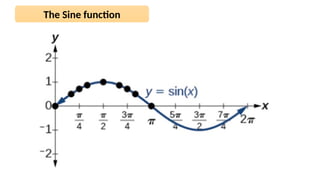
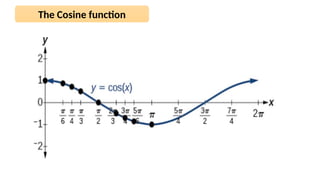
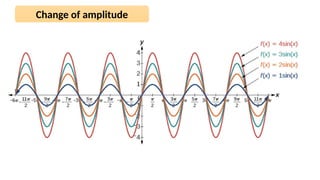
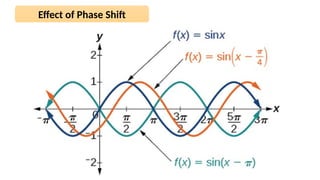
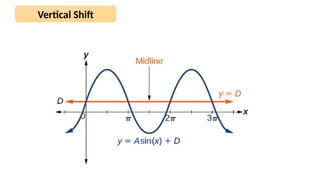
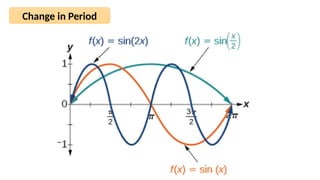
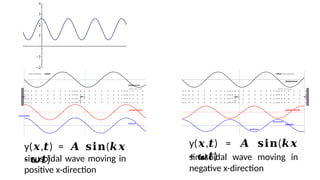
The document discusses the sinusoidal wave equation, including components such as amplitude, wave number, angular frequency, wavelength, period, speed, and direction. It provides a method for deriving these characteristics and offers sample problems with step-by-step solutions. The focus is on creating and analyzing wave equations for sinusoidal waves moving in both positive and negative directions.

1. Sinusoidal Wave Equation

2. Review

4. The Sine function

5. The Cosine function

6. Change of amplitude

7. Effect of Phase Shift

8. Vertical Shift

9. Change in Period

10. y( , ) = ( )
𝒙 𝒕 𝑨 𝐬𝐢𝐧 𝒌𝒙 𝝎𝒕 𝝓 sinusoidal wave
equation
where:
y = (Unit: m)
𝑑𝑖𝑠𝑝𝑙𝑎𝑐𝑒𝑚𝑒𝑛𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑝𝑎𝑟𝑡𝑖𝑐𝑙𝑒 𝑖𝑛 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑢𝑚
𝒌 = ( : rad/m)
𝑤𝑎𝑣𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑈𝑛𝑖𝑡
𝑨 = a ( : )
𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒 𝑈𝑛𝑖𝑡 𝑚
𝝎 = (Unit: rad/s)
𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑤𝑎𝑣𝑒
𝝓 = phase constant
If the displacement (y) of the wave is zero at t = 0 and x = 0,
then = 0. The sinusoidal wave equation is reduced to:
𝜙
y( , ) = ( )
𝒙 𝒕 𝑨 𝐬𝐢𝐧 𝒌𝒙 𝝎𝒕
Sinusoidal Wave Equation

11. y( , ) = (
𝒙 𝒕 𝑨 𝐬𝐢𝐧 𝒌𝒙
- )
𝝎𝒕
sinusoidal wave moving in
positive x-direction
y( , ) = (
𝒙 𝒕 𝑨 𝐬𝐢𝐧 𝒌𝒙
+ )
𝝎𝒕
sinusoidal wave moving in
negative x-direction

12. Steps in Finding the Characteristics of a Sinusoidal Wave
1. To get the sinusoidal wave’s amplitude, wavelength, period,
frequency, speed, direction and wave number, write down the
wave function in the form:
Use y( , ) = ( - ) ± or
𝒙 𝒕 𝑨 𝐬𝐢𝐧 𝒌𝒙 𝝎𝒕 𝝓 y( , ) =
𝒙 𝒕 𝑨 cos ( )
𝒌𝒙 𝝎𝒕
± 𝝓 for positive x-direction .
Use y( , ) = ( + ) ± or
𝒙 𝒕 𝑨 𝐬𝐢𝐧 𝒌𝒙 𝝎𝒕 𝝓 y( , ) =
𝒙 𝒕 𝑨 cos ( )
𝒌𝒙 𝝎𝒕
± 𝝓 for negative x-direction.
y( , ) = ( ) ±
𝒙 𝒕 𝑨 𝐬𝐢𝐧 𝒌𝒙 ∓ 𝝎𝒕 𝝓
or y( , ) =
𝒙 𝒕 𝑨 cos ( )
𝒌𝒙 𝝎𝒕 ± 𝝓

13. 2. The amplitude can be taken directly from the equation and is equal
to .
𝐴
3. Derive the period of the wave from the angular frequency: T =
4. Use = to get the frequency of the wave.
𝑓
5. The wave number can be found using the equation: =
𝑘
6. The wavelength can be derived from the wave number: =
7. The speed of the wave is: =
𝑣
y( , ) =
𝒙 𝒕 𝑨 (
𝐬𝐢𝐧 𝒌𝒙 ∓ 𝝎 )
𝒕
± 𝝓

14. Sinusoidal Wave Equation: Sample Problems
Find the:
a. amplitude
b. wave number
c. angular frequency
d. wavelength
e. period
f. speed of the wave
g. direction of the wave
h. frequency of the wave
1. A transverse wave on a string is described by the wave
function: y( , )= . ( . − .
𝒙 𝒕 𝟎 𝟐𝒎 𝒔𝒊𝒏 𝟔 𝟐𝟖 𝒙 𝟏 𝟓𝟕 )
𝒕

15. Sinusoidal Wave Equation: Sample Problems
a. amplitude A = 0.2 m
b. wave number k = 6.28 rad/m
c. angular frequency 𝝎 = 1.57 rad/s
d. wavelength = = = 1 m
e. period T = = = 4 s
f. speed of the wave = = = 0.25 m/s
𝑣
g. direction of the wave positive x-direction
h. frequency of the wave =
𝑓 = = 0.25 Hz
Solution
y( , ) =
𝒙 𝒕 .
𝟎 𝟐 𝒎 (
𝒔𝒊𝒏 .
𝟔 𝟐𝟖 −
𝒙 .
𝟏 𝟓𝟕 )
𝒕
y( , ) =
𝒙 𝒕 𝑨 (
𝐬𝐢𝐧 𝒌 -
𝒙 𝝎 ) ±
𝒕 𝝓

16. Sinusoidal Wave Equation: Sample Problems
Find the:
a. amplitude
b. wave number
c. angular frequency
d. wavelength
e. period
f. speed
g. direction
h. frequency
2. A wave travelling along a string is denoted by:
y( , ) = . ( . − . )
𝒙 𝒕 𝟎 𝟎𝟎𝟓 𝒎 𝐬𝐢𝐧 𝟖𝟎 𝟎 𝒙 𝟑 𝟎𝟎 𝒕

17. Sinusoidal Wave Equation: Sample Problems
a. amplitude A = 0.005 m
b. wave number k = 80.0 rad/m
c. angular frequency 𝝎 = 3.00 rad/s
d. wavelength = = = 0.0785 m
e. period T = = = 2.09 s
f. speed of the wave = = = 0.0.0375 m/s
𝑣
g. direction of the wave positive x-direction
h. frequency of the wave =
𝑓 = = 0.48 Hz
Solution
y( , ) =
𝒙 𝒕 .005
𝟎 𝒎 (
𝒔𝒊𝒏 8 −
𝒙 3. )
𝒕
y( , ) =
𝒙 𝒕 𝑨 (
𝐬𝐢𝐧 𝒌 -
𝒙 𝝎 ) ±
𝒕 𝝓

18. Sinusoidal Wave Equation: Sample Problems
a. frequency
b. angular frequency
c. wave number
d. wavelength
e. write the wave
equation
3. A sinusoidal wave travelling on a rope has a period of 0.025 s , speed of
30 m/s and an amplitude of 0.021525 m. At t = 0, the element of the
string has zero displacement and is moving in the +x-direction. Find the
following wave characteristics:

19. Sinusoidal Wave Equation: Sample Problems
What we know:
T = 0.025 s = 0
𝝓
v = 30 m/s moving towards positive x-direction
A = 0.21525 m
a. Frequency =
𝑓 = = 40 Hz
b. angular frequency T = =
𝝎 = = 251.2rad/s
c. wave number =
𝑣 k = = = 8.37 rad/m
d. Wavelength = = = 0.75 m
e. write the wave equation y( , ) =
𝒙 𝒕 𝑨 (
𝐬𝐢𝐧 𝒌 -
𝒙 𝝎 ) ±
𝒕 𝝓
y( , ) =
𝒙 𝒕 0.21525 m (
𝐬𝐢𝐧 8.37 –
𝒙 251.2 ) + 0
𝒕
y( , ) = 0.21525 m (8.37 – 251.2 )
𝒙 𝒕 𝐬𝐢𝐧 𝒙 𝒕
Solution: y( , ) =
𝒙 𝒕 .005
𝟎 𝒎 (
𝒔𝒊𝒏 8 −
𝒙 3. )
𝒕

20. EXERCISES