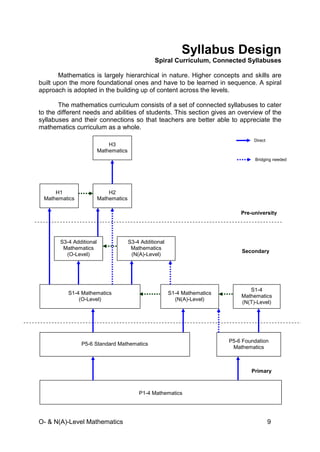
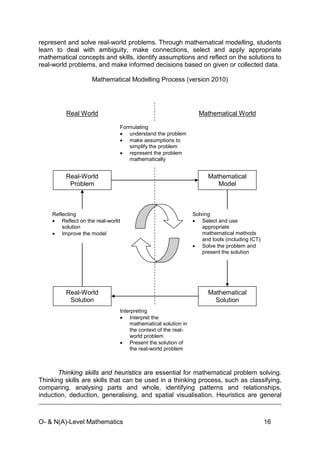
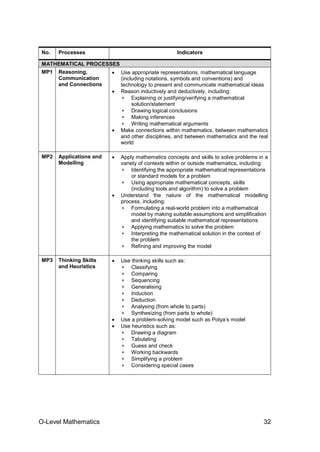
The document outlines the O- and N(A)-level mathematics teaching and learning syllabus for secondary students in Singapore, detailing its implementation starting from 2013. It emphasizes the importance of mathematics in fostering 21st-century skills and preparing students for a technologically-driven economy while providing a framework for differentiated learning pathways. The syllabus aims to enable all students to achieve mastery in mathematics and supports their continuous learning and application of mathematical concepts across different educational levels.