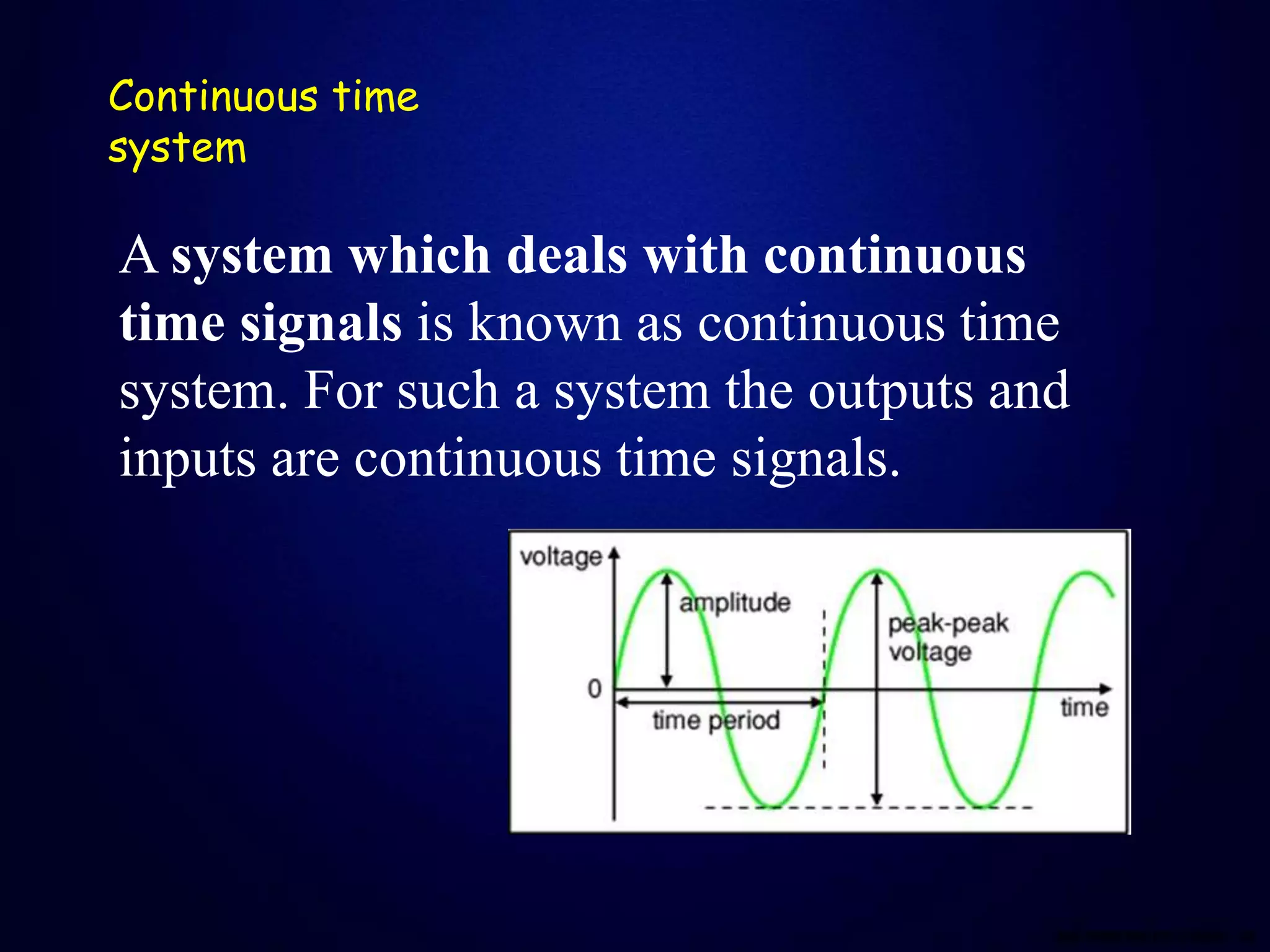
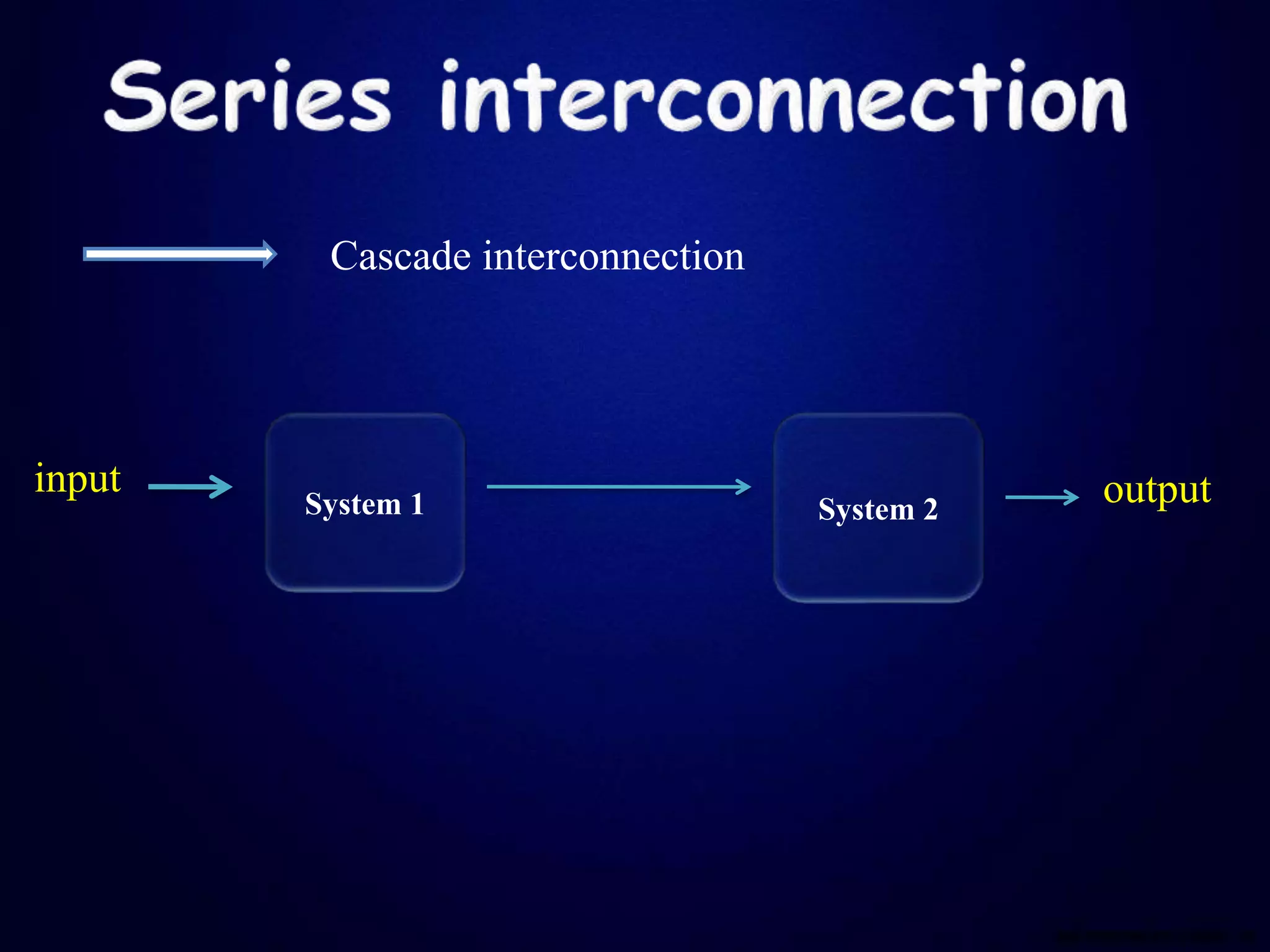
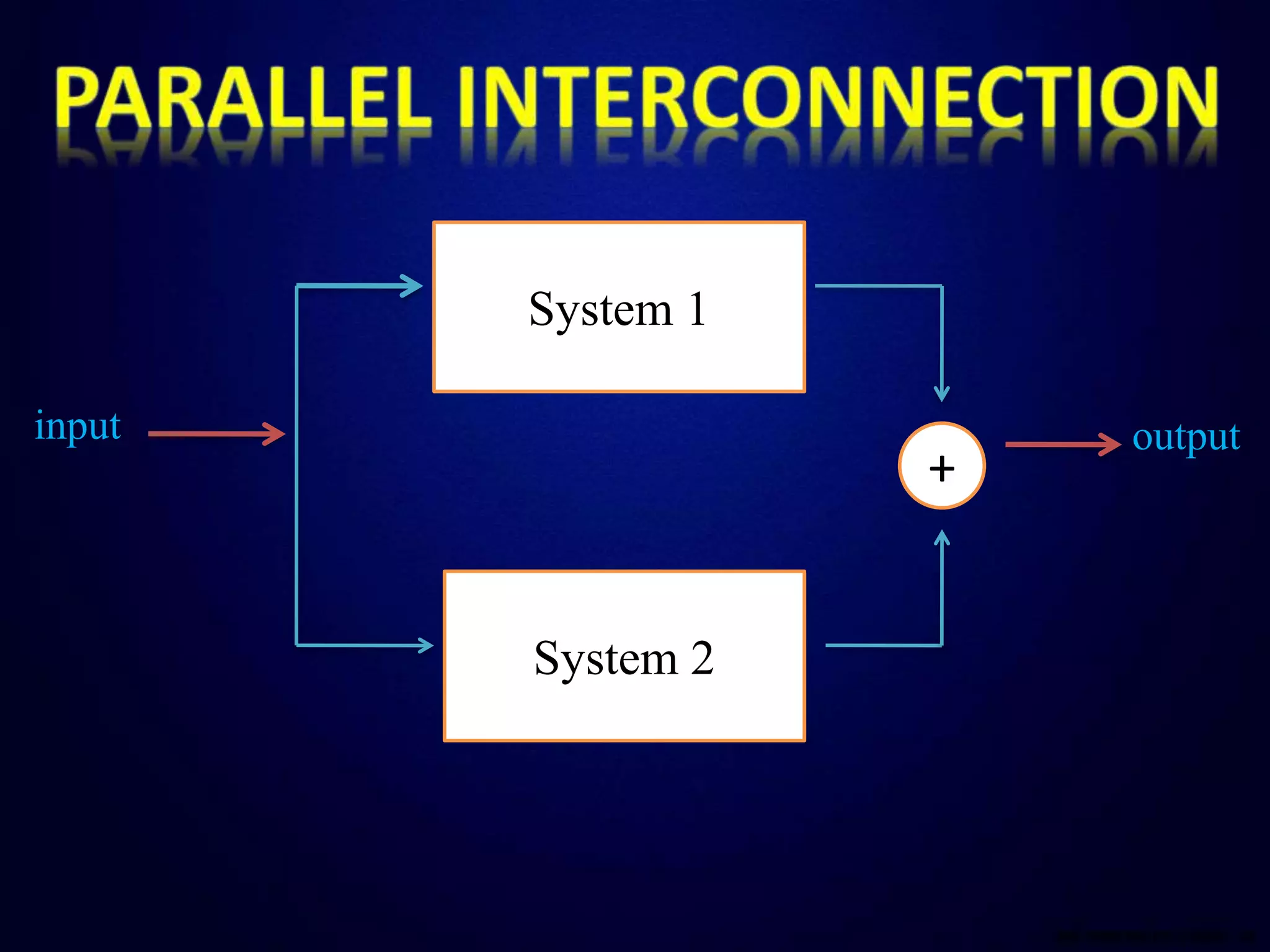
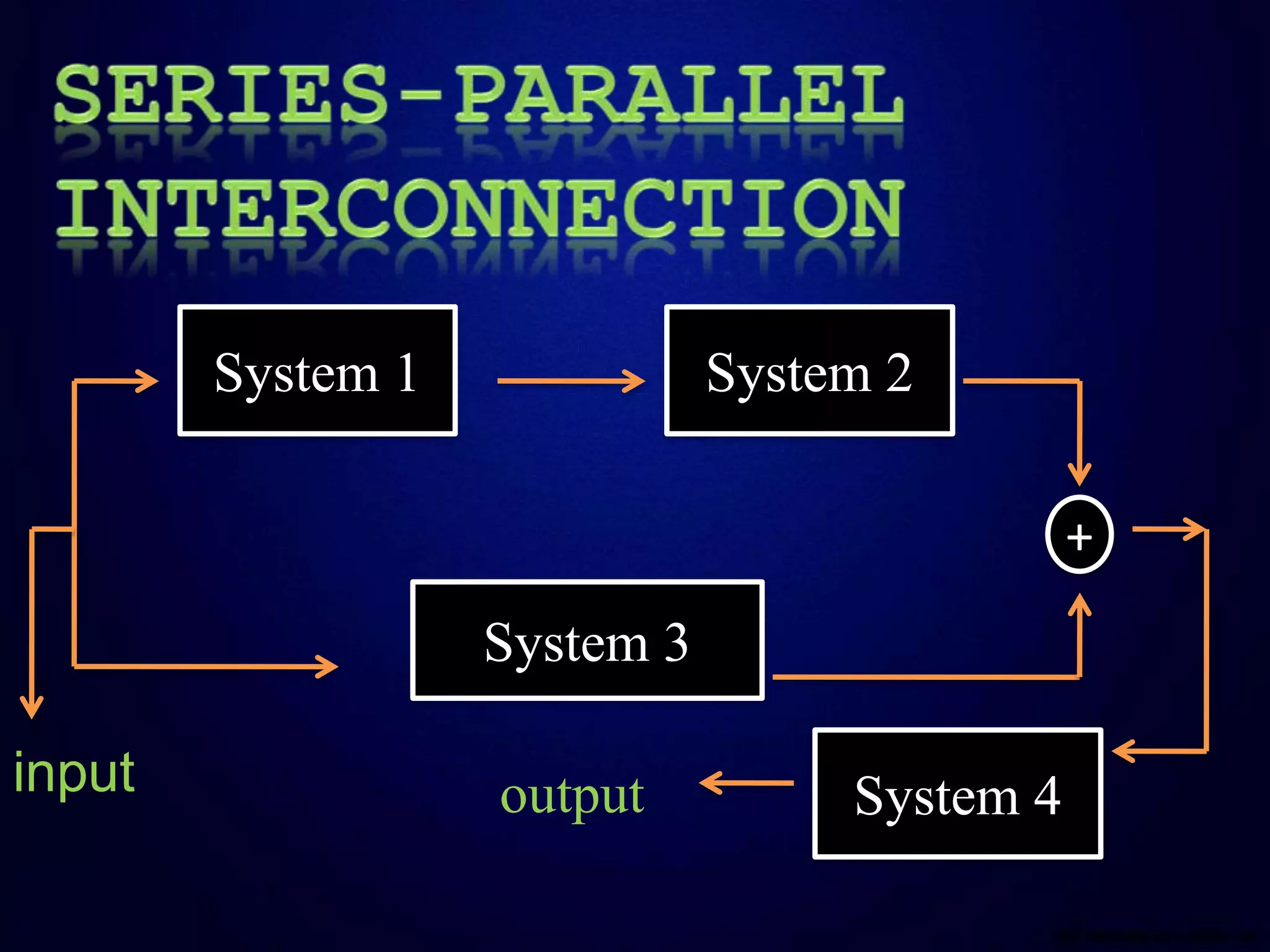
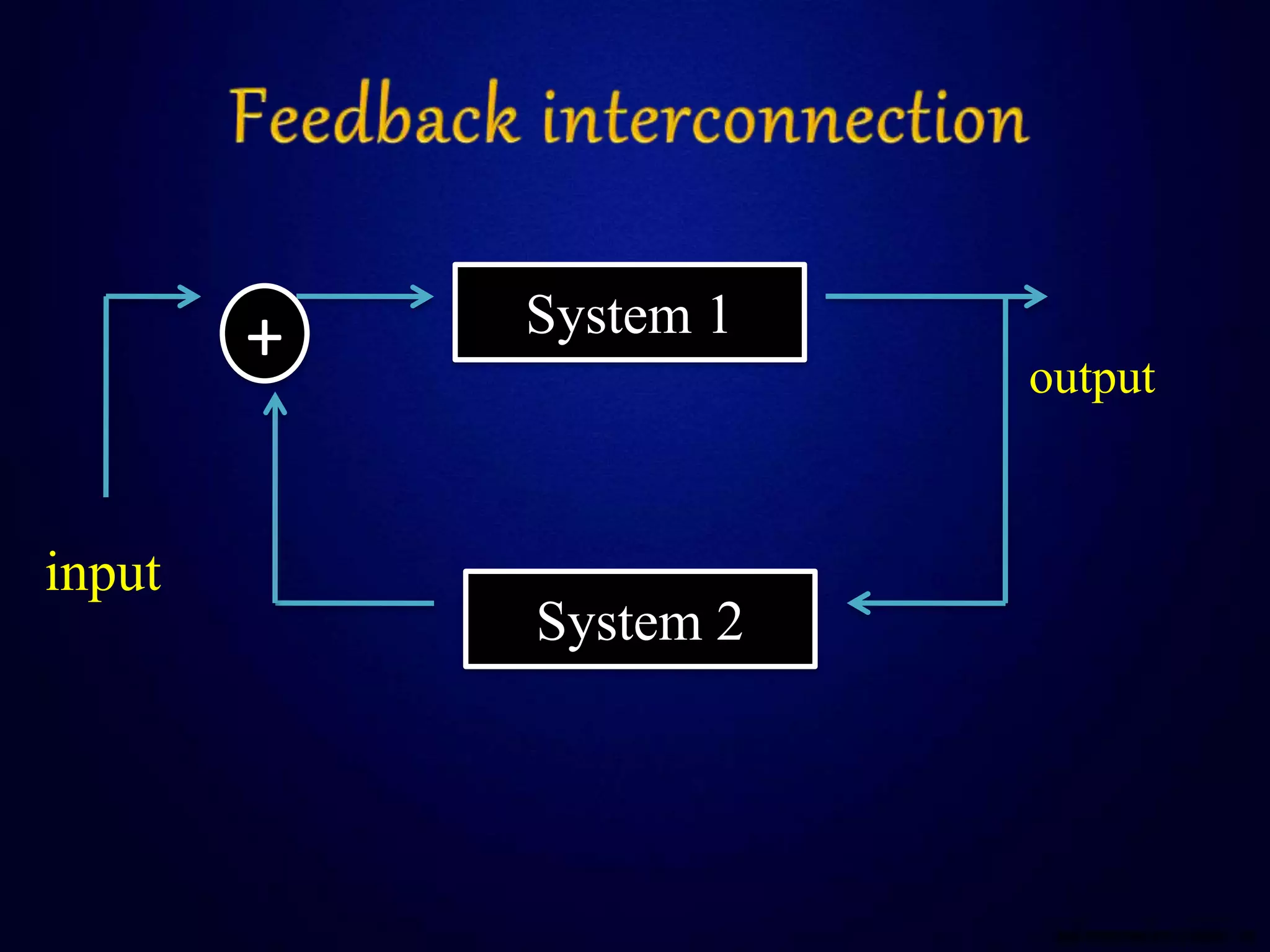
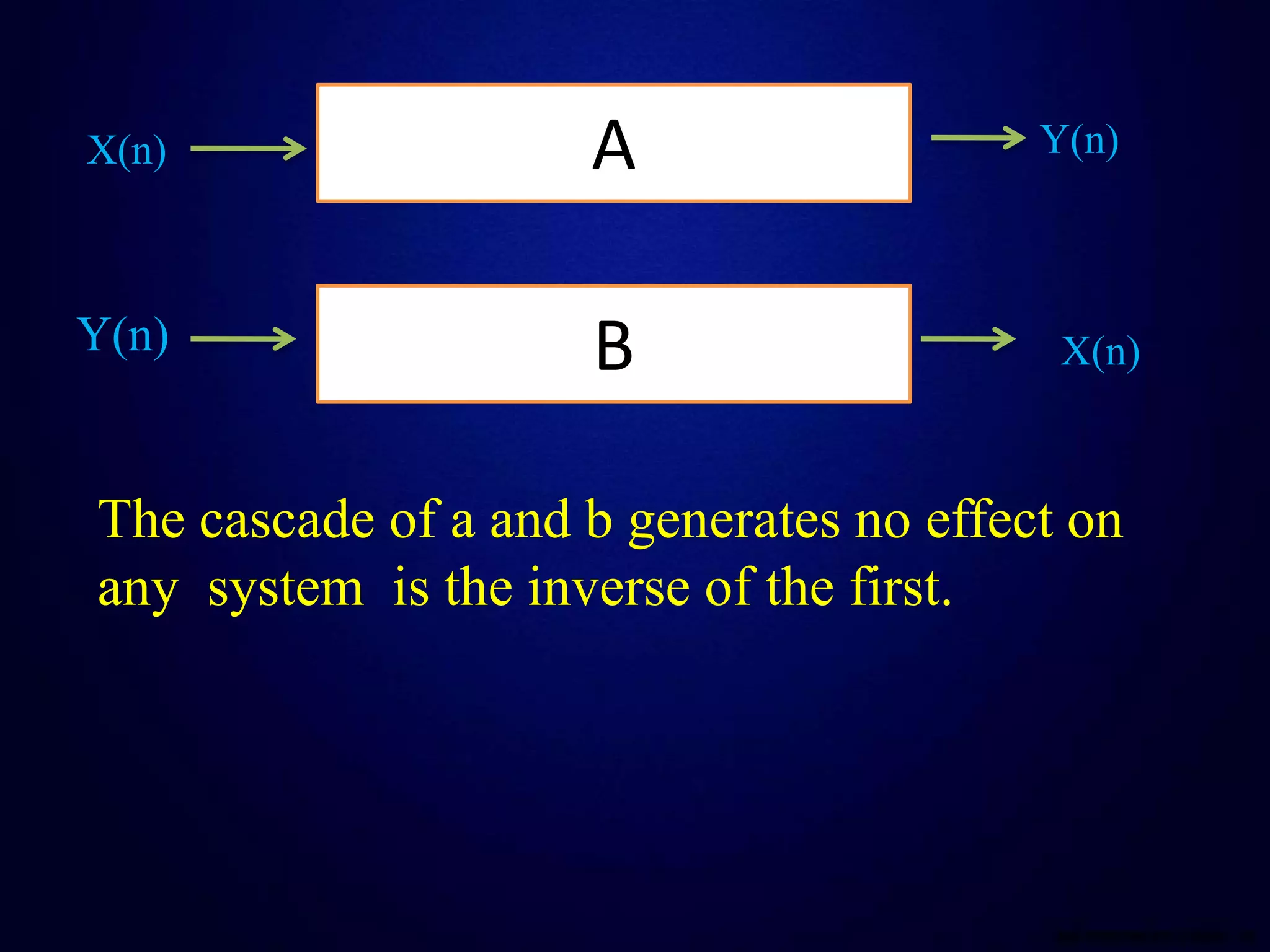
This document defines and compares continuous and discrete time systems. Continuous time systems deal with continuous signals as inputs and outputs, while discrete time systems deal with discrete signals. The document discusses different types of interconnections between systems including series, parallel, and series-parallel. It also outlines several basic properties of systems including memory, invertibility, causality, stability, time-invariance, and linearity. Memoryless systems only depend on the current input, while causal systems can compute the output using only past and present inputs. Stable systems have bounded outputs for bounded inputs. Time-invariant systems behave the same over time and linear systems follow superposition.

1. Honey Jose
EC B
NO:7

2. Contents:
Introduction
Continuous time system
Discrete time system
Interconnections
Series
Parallel
Series-parallel
Basic properties
Systems with and without memory
Invertibility and inverse systems
Causality
Stability
Time invariance
Linearity

3. Continuous time
system
A system which deals with continuous
time signals is known as continuous time
system. For such a system the outputs and
inputs are continuous time signals.

4. Such a system will be represented pictorially as
In figure
Continuous time systemX(t) Y(t)
X(t) is the input
Y(t) Is the output
X(t) Y(t)((input-output relation)

5. Discrete time system
Discrete time system deals with
discrete time signals. For such
a system the outputs and inputs
are discrete time signals.

6. Discrete time system can be depicted
As shown below
Discrete
time signal
X[n] Y[n]
Sometimes it will symbolically represented as follows
X[n] Y[n]

7. Interconnections of systems
A system is an interconnection of components
that act on input signals to produce output
signal
systeminput output

8. Cascade interconnection
System 1 System 2
input output

9. System 1
System 2
+
input output

10. System 1 System 2
System 3
+
input System 4output

11. System 1
System 2
+
input
output

12. Memory less
A system is memory less if the output at
Time ( t)or (n) only depends on the input
At time (t)or(n).
 Invertibility and inverse systems
A system a is invertible if there is another system
b ,such that when the output of a Is applied to b ,
the output of b is the input of a.

13. A
B
X(n) Y(n)
Y(n) X(n)
The cascade of a and b generates no effect on
any system is the inverse of the first.

14. A system is causal if the value of the
output at time t(or n)can be
computed by knowing only all the
values of input up to and including
time t(or n).

15. stability
A system is stable if up on a small
fluctuation in input , the fluctuations of the
output are bounded. A system is, bounded
input bounded output (BIBO)if and only if
when ever |x[n]|≤B1<∞ for all n , there
existsB2>0such that |y[n]|≤B2<∞for all
n(whereB1andB2are positive numbers).

16. Time invariance
A system is called time-invariant when
its behavior and characteristics are
fixed over time.More precisely, if
x[n]→y[n](x(t)→y(t))then for any n0(t0),
x[n−n0]→y[n−n0](x(t−t0)→y(t−t0)).A
system that is not time-invariant is
called time-varying.

17. linearity
A system is linear,if
x1(t)→y1(t) x2(t)→y2(t) implies
a1x1(t)+a2x2(t)→a1y1(t)+a2y2(t)
For all complex scalars a1,a2.This is
called the superposition property.

18. conclusion
Discussed basic concepts related to
continuous and discrete time
Signals and systems.
In developing some of the elementary ideas
related to systems , introduced
Block diagrams to facilitate our discussions
concerning the interconnection of systems.
Discussed abut the various properties.