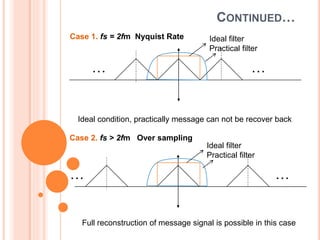
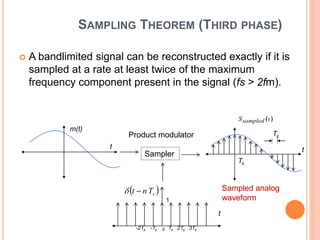
The document discusses the sampling theorem, highlighting that a bandlimited signal can be accurately reconstructed if sampled at a rate at least twice the maximum frequency component present. It outlines different scenarios based on guard bands and sampling rates, including cases of ideal and practical filters. Applications of this theorem include audio and video sampling, communication systems, and digital signal processing.

1. SAMPLING PROCESS

2. SAMPLING THEOREM (THIRD PHASE)
 A bandlimited signal can be reconstructed exactly if it is
sampled at a rate at least twice of the maximum
frequency component present in the signal (fs > 2fm).
Sampled analog
waveform
t
Ts
Ts
 
t
sampled
S
m(t)
t
Sampler
Product modulator
 
s
T
n
t 

t
0 Ts 2Ts 3Ts
-Ts
-2Ts
1

3. CONTINUED…
 
 s
T
n
t
 t
nw
b
t
nw
a
a o
n
o
n
n
n
o 







1
1
sin
cos
Fourier series representation of train impulse signal is
given as:
bn = 0; because train impulse signal is an even signal
s
s
s
s
o
T
dt
nT
t
T
a
T
1
)
(
1




s
s
o
s
s
n
T
tdt
nw
nT
t
T
a
T
2
cos
)
(
2




 
 s
T
n
t
 t
nw
T
T
s
s
s
n




1
cos
2
1

4. CONTINUED…
  )
(2
cos
2
)
(
cos
2
1
.
.
.









t
T
t
T
T
T
n
t s
s
s
s
s
n
s 


 
)
(2
cos
)
(
2
)
(
cos
)
(
2
)
(
1
.
.
.



 t
t
m
t
t
m
t
m
T
s
s
s


 
t
sampled
S
Spectrum
m(t)
fm
-fm
Modulation by
cos(s t)
Modulation by cos(2 s t)
 ]
)[
( 




n
s
T
n
t
t
m 
  
t
sampled
S

5. CONTINUED…
Spectrum
ws
-ws
   ]
[
cos s
s
s w
w
w
w
t
nw
FT



 


 
)
(2
cos
)
(
2
)
(
cos
)
(
2
)
(
1
.
.
.



 t
t
m
t
t
m
t
m
T
s
s
s


 
t
sampled
S
Spectrum
fm
-fm fs-fm fs
-fs fs+fm
-fs+fm
-fs+fm
…
…

6. CONTINUED…
fm
-fm fs-fm fs
-fs fs+fm
-fs+fm
-fs+fm
…
…
Gaurd band
Gaurd band = GB= fs – fm – fm = fs – 2fm
There are basically three different cases on guard band;
1. GB = 0 fs = 2fm
2. GB > 0 fs > 2fm
3. GB < 0 fs < 2fm

7. CONTINUED…
Ideal condition, practically message can not be recover back
Case 1. fs = 2fm Nyquist Rate
…
…
Case 2. fs > 2fm Over sampling
Full reconstruction of message signal is possible in this case
…
…
Ideal filter
Practical filter
Ideal filter
Practical filter

8. CONTINUED…
…
…
Case 3. fs < 2fm Aliasing effect
Interference of high frequency components
Recovery of original message signal is not possible
Ideal filter
Practical filter

9. APPLICATIONS
 Audio sampling
Video sampling
Communication systems
Digital signal processing
Speech sampling
 3D sampling
Digital Storage Oscilloscope (DSO)

10. THANK YOU