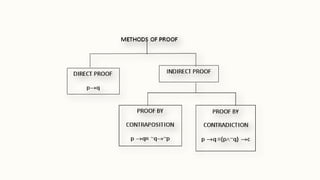
The document outlines the definitions and principles of even and odd integers, emphasizing that an integer n is even if it can be expressed as n = 2k and odd if n = 2k + 1. It describes the method of direct proof where one shows that if a hypothesis holds true, the conclusion must also be true, providing examples of proving theorems about integers. Additionally, it includes the concepts of prime and composite numbers, clarifying definitions through examples.

1. DIRECT PROOF

3. Basic Definitions
oAn integer n is even if and only if n is twice some
integer k.
– n is even an integer k such that n = 2k.
⇔ ∃
o An integer n is odd if and only if n is twice some
integer k plus 1.
– n is odd an integer k such that n = 2k + 1.
⇔ ∃
– Is -461 odd?
– If a and b are integers then is 4a + 10b is even? Yes 2(2a + 5b)
Yes 2(−151) + 1.

4. Direct Proof
o The implication p q can be proved by showing that if p is
true, the q must also be true.
o This shows that the combination p true and q false never
occurs. A proof of this kind is called a direct proof.

5. Method of Direct Proof
1. Express the statement to be proved in the form
“ x D, if P(x) then Q(x).”
∀ ∈ (This step is often done mentally.)
2. Start the proof by supposing x is a particular but arbitrarily
chosen element of D for which the hypothesis P(x) is true. (This
step is often abbreviated “Suppose x D and P(x).”)
∈
3. Show that the conclusion Q(x) is true by using definitions,
previously established results, and the rules for logical
inference.

6. A Direct Proof of a Theorem
o Prove that the sum of any two even integers is even.
o Formal Restatement: integers
∀ m and n, if m and n are even
then m + n is even.
o Starting Point: Suppose m and n are particular but arbitrarily
chosen integers that are even.
o To Show: m + n is even.
o If the existence of a certain kind of object is assumed or has been deduced then it can be given a
name, as long as that name is not currently being used to denote something else.

7. A Direct Proof of a Theorem

8. Direct Proof and Counterexample
o Give a direct proof of the theorem “If n is an odd integer, then n2
is odd.”
∀n P(n) → Q(n), where P(n) is “n is an odd integer” and Q(n) is “n2
is odd.”
By def. n = 2k + 1, where k is some integer.
To prove n2
is odd, take square of both sides
n2
= (2k + 1)2
= 4k2
+ 4k + 1 = 2(2k2
+ 2k) + 1
(it is one more than twice an integer).
Consequently, we have proved that if n is an odd integer, then n2
is an odd
integer.

9. A Direct Proof of a Theorem

10. Direct Proof and Counterexample
o Prime & Composite
– 6=2· 3 is a product of two smaller positive integers
– 7=1.7
– A positive integer that cannot be written as a product of two smaller positive
integers is called prime.