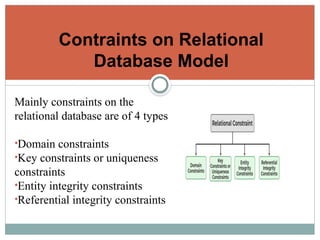
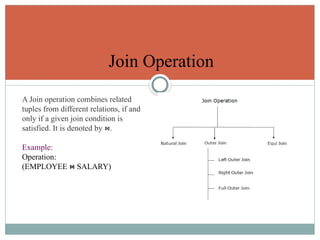
The document outlines the relational model in database management systems (DBMS), defining key concepts such as tables, attributes, tuples, and relational schemas. It describes relational algebra operations like select, project, and join, providing details on how these operations can be used to query and manipulate data. Furthermore, it explains various types of joins and relational constraints that ensure data integrity in a relational database.

1. M S . R . VA N I T HA
RDBMS-UNIT-II (23UITCC31)

2. Relational model can represent as a table with columns and rows.
Domain: it contains a set of atomic values that an attribute can take.
Attribute: it contains the name of a column in a particular table. Each attribute ai must
have a domain.
Relational instance: in the relational database system, the relational instance is
represented by a finite set of tuples. Relation instances do not have duplicate tuples.
Relational schema: A relational schema contains the name of the relation and name of all
columns or attributes.
Relational key: in the relational key, each row has one or more attributes. It can identify
the row in the relation uniquely.
Relational Model in DBMS

3. •Name of the relation is distinct from all other relations.
•Each relation cell contains exactly one atomic (single)
value
•Each attribute contains a distinct name
•Attribute domain has no significance
•Tuple has no duplicate value
•Order of tuple can have a different sequence
Properties of Relations

4. Mainly constraints on the
relational database are of 4 types
•Domain constraints
•Key constraints or uniqueness
constraints
•Entity integrity constraints
•Referential integrity constraints
Contraints on Relational
Database Model

5. Query is a question or requesting information. Query
language is a language which is used to retrieve
information from a database.
Query language is divided into two types −
•Procedural language
•Non-procedural language
Unary Relational Operations

6. Procedural Language
Relational algebra consists of a set of operations that take one or two relations as an input
and produces a new relation as output.
The different types of relational algebra operations are as follows −
• Select operation
• Project operation
• Rename operation
• Union operation
• Intersection operation
• Difference operation
• Cartesian product operation
• Join operation
• Division operation

7. Select Operation
It displays the records that satisfy a condition and is denoted by sigma
(σ). It is a horizontal subset of the original relation.
Syntax
The syntax for the select operation is as follows −
σcondition(table name)
Example:
σbranch=cse(student)
Output:
Reg
No
Branch Sectio
n
1 CSE A

8. Projection Operation
It displays the specific column of a table. It is denoted by pie (Π). It is a vertical subset of
the original relation. It eliminates duplicate tuples.
Syntax
The syntax of projection operation is as follows −
∏regno(student)
Example 1
∏regno(student)
Output:
RegNo
1
2
3

9. Rename Operation
It is used to assign a new name to a relation. It is denoted by ρ (rho).
Syntax
The syntax for rename operation is as follows −
ρnewname (tablename or expression)
Example
ρnewstudent (student)
Types of RENAME
Renaming can be used by three methods, which are as follows −
•Changing name of the relation.
•Changing name of the attribute.
•Changing both.

10. Union Operation
1. The UNION operation is commutative, that is :
A B = B A
∪ ∪
2. The UNION is associative, that means it is applicable to any number of relation.
A ( B C ) = ( A B ) C
∪ ∪ ∪ ∪
3. In SQL, the operation UNION is as same as UNION operation here.
4. Moreover, In SQL there is multiset operation UNION ALL.

11. Intersection Operation
1. The INTERSECTION operation is commutative, that is :
A ∩ B = B ∩ A
2. The INTERSECTION is associative, that means it is applicable to any number
of relation.
A ∩ ( B ∩ C ) = ( A ∩ B ) ∩ C
3. INTERSECTION can be formed using UNION and MINUS as follows:
A ∩ B = ((A ∪ B) - (A - B)) - (B - A)
4. In SQL, the operation INTERSECT is as same as INTERSECTION operation
here.
5. Moreover, In SQL there is multiset operation INTERSECT ALL.

12. Minus or Set Difference Operation
1. The SET DIFFERENCE operation is not commutative, that means :
A - B != B - A
2. In SQL, the operation EXCEPT is as same as MINUS operation here.
3. Moreover, In SQL there is multiset operation EXCEPT ALL.

13. Join Operation
A Join operation combines related
tuples from different relations, if and
only if a given join condition is
satisfied. It is denoted by .
⋈
Example:
Operation:
(EMPLOYEE SALARY)
⋈

14. Types of Join Operation
1. Natural Join: A natural join is the set of tuples of all combinations in R and S that are equal on their
common attribute names. It is denoted by . Example:
⋈
∏EMP_NAME, SALARY (EMPLOYEE SALARY)
⋈
2. Outer Join: The outer join operation is an extension of the join operation. It is used to deal with
missing information.
Example: (EMPLOYEE FACT_WORKERS)
⋈
3. Equi join: It is also known as an inner join. It is the most common join. It is based on matched data as
per the equality condition. The equi join uses the comparison operator(=)
Example:CUSTOMER PRODUCT
⋈

15. Types of Outer Join Operation
a. Left outer join:
•Left outer join contains the set of tuples of all combinations in R and S that are equal on their common
attribute names. In the left outer join, tuples in R have no matching tuples in S.
It is denoted by . Example:
⟕ EMPLOYEE FACT_WORKERS
⟕
b. Right outer join:
•Right outer join contains the set of tuples of all combinations in R and S that are equal on their
common attribute names. In right outer join, tuples in S have no matching tuples in R.
It is denoted by . Example:
⟖ EMPLOYEE FACT_WORKERS
⟖
c. Full outer join:
•Full outer join is like a left or right join except that it contains all rows from both tables.
•In full outer join, tuples in R that have no matching tuples in S and tuples in S that have no matching
tuples in R in their common attribute name.
•It is denoted by . Example:
⟗ EMPLOYEE FACT_WORKERS
⟗

16. Example Queries on Relational
Algebra
Suppose there is a banking database which comprises following tables :
Customer(Cust_name, Cust_street, Cust_city)
Branch(Branch_name, Branch_city, Assets)
Account (Branch_name, Account_number, Balance)
Loan(Branch_name, Loan_number, Amount)
Depositor(Cust_name, Account_number)
Borrower(Cust_name, Loan_number)
Query : Find the names of all the customers who have taken a loan from the bank and also have an account at the bank.
Solution:
Step 1 : Identify the relations that would be required to frame the resultant query.
First half of the query(i.e. names of customers who have taken loan) indicates “borrowers” information.
So Relation 1 —–> Borrower.
Second half of the query needs Customer Name and Account number which can be obtained from Depositor relation.
Hence, Relation 2——> Depositor.
Step 2 : Identify the columns which you require from the relations obtained in Step 1.