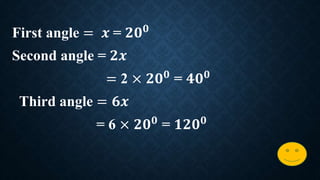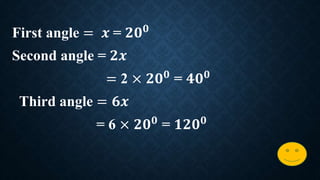
1) The lesson plan discusses solving problems involving ratios of quantities in triangles. 2) It provides examples of finding side lengths when given a ratio of sides and perimeter, and finding angles when given a ratio of angles. 3) The homework problem asks the student to find the angles of a triangle given the angles are in the ratio 2:3:4.

1. LESSON PLAN
Submitted by
Greeshma George

3. Three Quantities
If three quantities are in the
ratio 𝒂 ∶ 𝒃 ∶ 𝒄 , then there is a
quantity 𝒙 such that first is 𝒂𝒙
, second is 𝒃𝒙 and third is 𝒄𝒙

4. Problem 1
The sides of a triangle are in the
ratio 3:5:7 and its perimeter is 45
centimetres. What are the length
of the sides?

5. SOLUTION
Three sides are 3𝑥 , 5𝑥 𝑎𝑛𝑑 7𝑥
Perimeter = 45 centimetres
Then , 3𝑥 + 5𝑥 + 7𝑥 = 45
15𝑥 = 45
𝑥 = 45
15
𝑥 = 3

6. Then the sides are
3𝒙 = 3 × 3 = 9cm
5𝒙 = 5 × 3 = 15cm
7𝒙 = 7 × 3 = 21cm

7. Problem 2
The angles of a triangle are
in the ratio 1 : 3 : 5. How
much is each angle?

8. Solution
The first angle = 𝒙
The second angle = 𝟑𝒙
The third angle = 𝟓𝒙
Sum of angles of a triangle = 𝟏𝟖𝟎 𝟎
Then, x + 3x + 5x = 𝟏𝟖𝟎 𝟎
𝟗𝒙 = 𝟏𝟖𝟎 𝟎
𝒙 =
𝟏𝟖𝟎 𝟎
𝟗
= 𝟐𝟎 𝟎

9. First angle = 𝒙 = 𝟐𝟎 𝟎
Second angle = 𝟑𝒙
= 3 × 𝟐𝟎 𝟎
= 𝟔𝟎 𝟎
Third angle = 𝟓𝒙
= 5 × 𝟐𝟎 𝟎
= 𝟏𝟎𝟎 𝟎

10. Problem : 2
The outer angle of a triangle are
in the ratio 5 : 6 : 7 . What are
the angles?

11. Solution
The outer angles of a triangle are 5𝑥 , 6𝑥, 7𝑥
Sum of outer angles of a triangle are 3600
5𝑥 + 6𝑥 + 7𝑥 = 3600
18𝑥 = 3600
𝑥 =
3600
18
= 200

12. The angles of a triangle are in
the ratio 1 : 2 : 6. How much
is each angle?

13. The first angle = 𝑥
The second angle = 2𝑥
The third angle = 6𝑥
Sum of angles of a triangle = 1800
Then, x + 2x + 6x = 1800
9𝑥 = 1800
𝑥 =
1800
9
= 200

14. First angle = 𝒙 = 𝟐𝟎 𝟎
Second angle = 𝟐𝒙
= 2 × 𝟐𝟎 𝟎
= 𝟒𝟎 𝟎
Third angle = 𝟔𝒙
= 6 × 𝟐𝟎 𝟎 = 𝟏𝟐𝟎 𝟎

15. HOMEWORK
If the angles of a triangle are in
the ratio 2 : 3 : 4. What are the
angles?