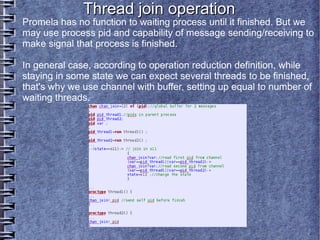
The document discusses modeling a program as a multi-threaded stochastic automaton and its equivalent transformation to a PROMELA model. It describes representing the program states, transitions, and operations as a mathematical abstraction called a finite automaton. The model can be extended to include additional features like events, messaging, threading and resource blocking to more accurately model modern software systems at a low level of abstraction. The model and its object-oriented implementation in Java are presented, along with the ability to describe it as an XML file for graphical representation and code generation. Abstract state machines are also briefly discussed as another formal modeling technique.

1. МОДЕЛЬ ПРОГРАММЫ В ВИДЕ
МНОГОПОТОЧНОГО
СТОХАСТИЧЕСКОГО АВТОМАТА И ЕЕ
ЭКВИВАЛЕНТНОЕ
ПРЕОБРАЗОВАНИЕ В МОДЕЛЬ НА
ЯЗЫКЕ PROMELA
MODEL OF A PROGRAM AS MULTI-
THREADED STOCHASTIC AUTOMATON
AND ITS EQUIVALENT
TRANSFORMATION TO PROMELA MODEL
International Workshop on Program Understanding
Staroletov Sergey, Altai STU

2. Model based developing and testing
Model based developing – is a
modern technology to developing software
which are firstly focuses on the model
developing, not on algorithmic and computation
concepts
Model based testing – technology of
software testing bases on
comparation the model and system
under test during the work, generation
test cases by the model,and changing
the system to the model for studying its
properties.

3. Finite automaton
Mathematical abstraction, which model discrete changing of states
from finite set depends of input symbol or event
How we can describe automaton
-The graph of transitions
-The table of transitions
-As a set of the sets and transition
functions
-As a set of cooperating classes
(object oriented way)
Applying: (*)
-Syntax analysis
-Regular expressions matching
-Modeling of logic of the work of
algorithm for imperative language
* Graph Theory Techniques in Model-Based Testing. Harry Robinson

4. Windows Workflow foundation
Projecting the program on the basis of assigning states
Object oriented realization of finite automaton
“Switch-technology”
“Automaton programming”
Example of control program
terminal for payments
(course work)

5. Extending of finite automaton
Why to extend finite automaton?
Model is bigger and complex=> describe the system more adequate
=> we can study more properties of a model
● Kripke structure
Extend of automaton by adding the set of atomic predicates
Which are true in states
Applying: backend в ModelChecking
● Probability automaton
Extend of automaton with adding transitions with probabilities
Applying: modeling of users's work
Extended automaton with support of events, messaging, threading and
●
blocking common resourses.
Author's extend for modeling component of modern interoperable system
for low level of abstraction

6. Author's model features
- Following to principles MDD and MBT
- Extended finite automaton as a model of
component of system, our extends includes
multi-threading, sending and receiving the
messages,blocking and unblocking common
resourses
- The system is set of automatons, each of them
modeling component of the system
- Possibility to object-oriented realization of
automaton to projecting program firstly based of
The states
- Designed for testing.

7. Предлагаемая модель в виде
состояний, переходов и операций
A=( S ,Trans ,Op ) ,
where
S - the set of states, allocated by developer;
Trans=S  S× E * - mapping, it defines the transition
with possibility of events generation;
E - set of events, is defined by state to which
transition are performed, and its probability of
occurrence;
*
Op={ fork , join , send , receive , block , unblock }×E - set
of operations in extended automaton discussed below
with possible related events.

8. Operations
We staying in the state. We can
(with some probability)
Make transition to another state
Or apply the operation
Create the thread : P×S  S×T 
fork 
Wait the thread join : P× S×T ×S ×T   S ×T
parent fin slave

parent
Send the message send : S×T ×P S × Msg∨E
Wait for a message receive : S×T ×P× Msg  S∨ E
Block the common resourse block : S ×T × N ×P× Res S ×1×Res ∨ E
Unblock the common unblock : S×1× Res×P  S ×N ×Res ∨ E
resource

9. Object-oriented model on Java
Why we need that model?
Describe states, operations and transitions as classes.
Model = interoperation of objects with given attributes
The interoperational logic already been realized in classes,
The business logic implements as call of user code
in states, transitions and operations and interfaces for this have been
descibed.
Features;
- States with user's code
- Transitions with probabilities),by guard or as
written in user code
- Applying operations in states
- Self system to sending-receiving messages
And resource blocking
- Mapping model threads to Java threads
-Support of distributive work with network
through XML-RPC

10. Object-oriented model on Java
public static void main(String[] args) {
//Создать список компонентов
List<Component> components=new LinkedList<Component>() ;
//Создать состояния, зададим их параметры позже
State state1=new State(),state2=new State(),state3=new State(),state4=new State(),state5=new State() ;
//Создать компонент
Component component1=new Component() ;
//Создать переход в состояние state2, без событий с вероятностью 1.0
Transition transition12=new Transition(state2, null, 1.0, "transition 1->2");
//Задать параметры состояния: главный поток компонента, название-state1
//нет подавтомата, начальное состояние=true, конечное состояние=false
//переходы из состояния- transition12, операций из состояния нет.
state1.setParams(component1.getMainThread(),"state1", null, true, false, new Transition[] { transition12}, null) ;
//Задать код, выполняющийся в состоянии state1
state1.setCode(new IStateCodeExecutor() {
@Override
public void execute(Component currentComponent,
Thread currentThread, State currentState) {
System.out.println("Зашли в состояние "+currentState.getName()) ;
}
},
new IStateCodeExecutor() {
public void execute(Component currentComponent,
Thread currentThread, State currentState) {
System.out.println("Выходим из состояния "+currentState.getName()) ;
}}) ;
//в state2: fork и создание потока с первоначальным состоянием state3, и
//продолжением главного потока в state5
//Создать подавтомат для потока с первоначальным состоянием state3
//и заключительным в state4
SubAutomaton subAutomatonThread2=new SubAutomaton("thread_subautomaton", state3, new State[]{state4},null) ;
//создать описание потока thread2, с подавтоматом subAutomatonThread2
//и предком в виде главного потока компонента
dissertation.Thread thread2=new dissertation.Thread("thread2", subAutomatonThread2,component1.getMainThread()) ;
//создать операцию Fork (создание потоков) для потока thread2 c переходом //основного потока в состояние state5
после создания без событий с //вероятностью 1.0
Fork operationForkState2=new Fork(new dissertation.Thread[] {thread2}, null,1.0,state5) ;
//установить параметры для state2- передать туда операцию создания потока
state2.setParams(component1.getMainThread(),"state2", null, false, false, null, new Operations[] {operationForkState2}) ;
...
//Установить состояния для компонента

11. XML description of a model
We can describe model as XML tags
By XML description from attribute or graphical editor we cancreate
graphic notation and generate object oriented automaton
code on Java

12. Abstract state machines
ASM defines by alphabet  (consists of name of functions), initial state (initial
value of a function), transition rules and initial rule.
Transition rules defined as:
1. f  s 1 ... s n :=t - in the next state the value of function f on the set of arguments
s 1 ... s n is assigned to t .
2. P seq Q - rule P is running after rule Q .
3. P par Q - rules P and Q is running in parallel.
4. if  then P else Q - if =true , proceed to run P , else proceed to run Q .
5. let x =t in P - assign the t value to local variable x and proceed to run P
(area of existence x after running P is ended).
6. forall x with  do P - proceed to run P in parallel for all x , satisfies  (area of
existence x after running P is ended).
7. choose x with fi do P - choose x satisfies  non-determinately and proceed to
run P .
8. skip - empty rule.
9. r t 1 ... t n  - call of the rule r with parameters t 1 ... t n .
Theorem: Every parallel algorithm is behaviorally equivalent to
an ASM *
With using ASM theory we can prove that our object-oriented
automaton Java model can model a wide set of algorithms
included parallel and distributive algorithms with finite number
of processes.
Proof: By developing interpreter for ASM machine
*Blass,A. Abstract State Machines Capture Parallel Algorithms: Correction and Extension / Andreas Blass, University of Michigan,
Yuri Gurevich, Microsoft Research- http://www.math.lsa.umich.edu/~ablass/corr-final.pdf

13. Model checking approach
applying to our model
Model checking is a static verifying method to check model behavior.
Popular, powerful and highly documented tool that's providing
model checking approach is SPIN.
SPIN uses special functional language called 'Promela*' as an input
model language.
* Concise Promela Reference/ Rob Gerth, 1997. http://spinroot.com/spin/Man/Quick.html

14. Model checking approach
applying to our model
SPIN modes:
- Random model activity simulation
Resolve non-determinism as given seed value
- Interactive simulation
Ask user for the choice for non-determinism
- Guided simulation
Re-simulate previous stored simulation or contra-primer
by LTL check
- LTL(Linear time temporal logic) predicate check
Temporal logic is logic with time, is used to
ask model to check that's value of predicate with desired
variables is true in all states(“globally”) or some predicate
is true at least in one state than another predicate is true.
Check result: proof that's all ok or return trace with
:
contra-primer

15. Model checking approach
applying to our model
Research result: for our automaton stochastic model
exists equivalent Promela model
Testing process:
Testing environment
XML model Temporal logic predicate Verification results
Promela model
Object oriented Spin verifier
model
Now we go dip into building Promela model from our model
with states, transitions and operations.

16. Realization of finite automaton on
Promela language

17. Non-deterministic transitions
Improving adequacy: if we have transition with
probability we can generate that count of the same
lines with state changing to make correct probability of
transition by the probability definition

18. Thread creation operation
Entities in the Promela language which are running in parallel,
are called processes, but in any time any process can run
another process, so in fact they are threads.
For main thread in our model we must generate its main
process in Promela which will make transitions from states to
another states, and its corresponded process must be marked
by “active” modifier, which means that this process running at
the start of modeling. Other processes must be generated by
the threads bodies with logics as subautomatons.

19. Thread join operation
Promela has no function to waiting process until it finished. But we
may use process pid and capability of message sending/receiving to
make signal that process is finished.
In general case, according to operation reduction definition, while
staying in some state we can expect several threads to be finished,
that's why we use channel with buffer, setting up equal to number of
waiting threads.

20. Messaging,send and receive
For receiving messages first of all we must create global channel
and enumeration type with message identifiers
For ordinary messages synchronous channels (with 0 as the size of
buffer) are used. For receiving messages with the “and” type we
need buffered channel (as shown in previous example). Sending
and receiving process is implemented by standard Promela
operators («!» and «?»), and after that operation next state is
chosen.

21. Blocking and unblocking resource
Assume global variable as shared resource. Due to Plomela language this
expression
(r==0)
at r≠0 stopped current process until r will not be 0 as a result of another
process that changed this value. BlockResource and UnblockResource are
based on that expression.

22. Studying model properties
Now we can verify some model properties with using static checking
1. All states in model are reachable?
- ∀ si ∈S doing Sping LTL formula checking with trying to make
a contra-primer for state !=si .
- if contra-primer found, si is reached and we can find the path
from initial state to si .
2. Is state reach from some chosen state?
- We like to test, if s x ∈S reached from s y ∈S
- Trying to make a contra-primer for LTL predicate
state≠s y U G state≠s x  , where U - temporal operator “Until”, аnd
G – temporal operator “Global” (for all states)
- If contra-primer found, we can find the path from s y to s x .

23. Studying model properties
Connectivity point – user's made set of linked sets of states
from one automaton/subautomaton/thread body to another
set of states. cp∈CP : { s A1 , s A2 ,... s An } ↔{ s B1 , s B2 ,... s Bm } .
Checking of connectivity points is verifying LTL predicate
G (( state A == s A1 || state A == s A2 ||...|| state A == s An ) ->
( state B == s B1 || state B == s B2 ||...|| state B == s Bm )).

24. Testing artifacts
Message chart digram Stack of transitions, operations and errors
Computed probabilities

25. МОДЕЛЬ ПРОГРАММЫ В ВИДЕ
МНОГОПОТОЧНОГО
СТОХАСТИЧЕСКОГО АВТОМАТА И ЕЕ
ЭКВИВАЛЕНТНОЕ
ПРЕОБРАЗОВАНИЕ В МОДЕЛЬ НА
ЯЗЫКЕ PROMELA
Q/A session
MODEL OF A PROGRAM AS MULTI-
THREADED STOCHASTIC AUTOMATON
AND ITS EQUIVALENT
TRANSFORMATION TO PROMELA MODEL
International Workshop on Program Understanding
Staroletov Sergey, Altai STU