Propositional equality, identity types, and computational paths

What is a Proof of an Equality? Brouwer–Heyting–Kolmogorov for Equality The Functional Interpretation of Propositional Equality N
Propositional Equality, Identity Types
and Computational Paths
Ruy de Queiroz
(joint work with Anjolina de Oliveira)
Centro de Inform´atica
Universidade Federal de Pernambuco (UFPE)
Recife, Brazil
Univ. Lisboa
25 Jul 2017
Ruy de Queiroz (joint work with Anjolina de Oliveira)
Centro de Inform´atica Universidade Federal de Pernambuco (UFPE) Recife, Brazil
Propositional Equality, Identity Types and Computational Paths

Homotopy Type Theory
Univalent Foundations of Mathematics
Institute for Advanced Study, Princeton
approx. 600p.
Open-source book: The Univalent Foundations Program
27 main participants. 58 contributors
Available on GitHub. Latest version October 3, 2016

“Homotopy type theory is a new branch of mathematics that
combines aspects of several different ﬁelds in a surprising
way. It is based on a recently discovered connection
between homotopy theory and type theory. Homotopy
theory is an outgrowth of algebraic topology and
homological algebra, with relationships to higher category
theory; while type theory is a branch of mathematical logic
and theoretical computer science. Although the
connections between the two are currently the focus of
intense investigation, it is increasingly clear that they are
just the beginning of a subject that will take more time and
more hard work to fully understand. It touches on topics as
seemingly distant as the homotopy groups of spheres, the
algorithms for type checking, and the deﬁnition of weak
∞-groupoids.”

Origins of Research Programme
Vladimir Voevodsky, (IAS, Princeton) (Fields Medal 2002)
1st
(?) use of term ‘homotopy λ-calculus’: tech report Notes on
homotopy λ-calculus, (Started Jan 18, Feb 11, 2006)
Steve Awodey (Dept Phil, CMU)
1st
(?) use of term ‘homotopy type theory’: Eighty-sixth Peripatetic
Seminar on Sheaves and Logic, Nancy, 8–9 September 2007

Henk Barendregt on the Evolution of Type Theory
“Type theory as coming originally from Whitehead-Russell
and simplified and essentially extended by Ramsey
(simplifying), Church (adding lambda terms), de Bruijn
(adding dependent types), Scott (adding inductive types
with recursion), Girard (adding higher order types),
Martin-Löf (showing the natural position and power of
intuitionism) all lead to proof-checking based on type theory
with successes like the full formalization of the 4CT and the
Feit-Thompson theorem by Gonthier and collaborators and
the forthcoming one of the Kepler conjecture by Hales and
collaborators.
Now, there are some difficulties with types (...). For this
reason there is work in progress by Voevodsky and
collaborators to modify this theory.”
(Barendregt 2014, FOM list)

HoTT Approach to Spaces: New Proofs
“Homotopy type theory is a synthetic theory of ∞-groupoids” (Michael Shulman)
“Progress in synthetic homotopy theory:
• π1(S1
) = Z (Shulman, Licata)
• πk (Sn
) = 0 for k < n (Brunerie, Licata)
• πn(Sn
) = Z (Licata, Brunerie)
• The long exact sequence of a ﬁbration (Voevodsky)
• The Hopf ﬁbration and π3(S2
) = Z (Lumsdaine, Brunerie)
• π4(S3
) = Z2 (Brunerie – almost)
• The Freudenthal suspension theorem (Lumsdaine)
• The Blakers–Massey theorem (Lumsdaine, Finster, Licata)
• The van Kampen theorem (Shulman)
• Whitehead’s theorem for n-types (Licata)
• Covering space theory (Hou)
Some of these are new proofs.”
(Homotopy type theory: towards Grothendieck’s dream, Michael
Shulman, 2013 International Category Theory conference, Sydney.)

Geometry and Logic
Alexander Grothendieck
Alexander Grothendieck
b. 28 March 1928, Berlin, Prussia, Germany
d. 13 November 2014 (aged 86), Saint-Girons, Ari`ege, France

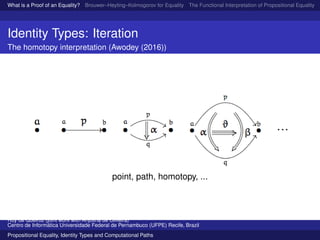
Geometry and Logic
Alexander Grothendieck: The Homotopy Hypothesis
. . . the study of n-truncated homotopy types (of
semisimplicial sets, or of topological spaces) [should
be] essentially equivalent to the study of so-called
n-groupoids. . . . This is expected to be achieved by
associating to any space (say) X its “fundamental
n-groupoid” Πn(X).... The obvious idea is that
0-objects of Πn(X) should be the points of X,
1-objects should be “homotopies” or paths between
points, 2-objects should be homotopies between
1-objects, etc. (Grothendieck 1983)
homotopy types ←→ ∞-groupoids

Geometry and Logic
Spaces
Approaching the notion of space in mathematics:
1 topological spaces
2 metric spaces
3 manifolds
4 schemes
5 stacks
6 homotopy spaces (starts from points and paths, thus, less
committed to set-theoretic foundations)

Geometry and Logic
Vladimir Voevodsky
“From an observation by Grothendieck:
formalism of higher equivalences (theory of grupoids)
=
homotopy theory (theory of shapes up to a
deformation)
combined with some other ideas leads to an encoding of
mathematics in terms of the homotopy theory. Unlike the usual
encodings in terms of set theory this one respects
equivalences.”

Type Theory and Homotopy Theory
Steve Awodey: a calculus to reason about abstract homotopy
“Homotopy type theory is a new field devoted to a recently discovered
connection between Logic and Topology – more specifically, between
constructive type theory, which was originally invented as a
constructive foundation for mathematics and now has many
applications in the theory of programming languages and formal proof
verification, and homotopy theory, a branch of algebraic topology
devoted to the study of continuous deformations of geometric spaces
and mappings. The basis of homotopy type theory is an interpretation
of the system of intensional type theory into abstract homotopy
theory. As a result of this interpretation, one can construct new kinds
of models of constructive logic and study that system semantically,
e.g. proving consistency and independence results. Conversely,
constructive type theory can also be used as a formal calculus to
reason about abstract homotopy.”
(A proposition is the (homotopy) type of its proofs, Jan 2016.)

Algebraic Structure: Groupoids
Steve Awodey
“A groupoid is like a group, but with a partially-deﬁned
composition operation. Precisely, a groupoid can be deﬁned as
a category in which every arrow has an inverse. A group is thus
a groupoid with only one object. Groupoids arise in topology as
generalized fundamental groups, not tied to a choice of
basepoint.”
(Type Theory and Homotopy, 2010.)
“A groupoid is a generalized group, with the multiplication being
only a partial operation – or equivalently, a category in which
every arrow has an inverse.”
(Univalence as a Principle of Logic, 2016.)

Equality in λ-Calculus: deﬁnitional vs. propositional
Proofs of equality as paths
Church’s (1936) original paper:
NB: equality as the reﬂexive, symmetric and transitive closure of
1-step contraction: rewriting paths. An algebra of paths (with α, β, η,
µ, ν, ξ, ρ, σ, τ)? E.g. σ(σ(r)) = r, τ(τ(t, r), s) = τ(t, τ(r, s)).

Equality in λ-Calculus: definitional vs. propositional
Proofs of equality: Paths
Definition (Hindley & Seldin 2008)
P is βη-equal or βη-convertible to Q (notation P =βη Q) iff Q is
obtained from P by a finite (perhaps empty) series of
β-contractions, η-contractions, reversed β-contractions,
reversed η-contractions, or changes of bound variables. That is,
P =β Q iff there exist P0, . . . , Pn (n ≥ 0) such that
P0 ≡ P, Pn ≡ Q,
(∀i ≤ n − 1) (Pi 1β Pi+1 or Pi+1 1β Pi
or Pi 1η Pi+1 or Pi+1 1η Pi
or Pi ≡α Pi+1).

The Functional Interpretation of Equality
Sequences of contractions
(λx.(λy.yx)(λw.zw))v 1η (λx.(λy.yx)z)v 1β (λy.yv)z 1β zv
(λx.(λy.yx)(λw.zw))v 1β (λx.(λw.zw)x)v 1η (λx.zx)v 1β zv
(λx.(λy.yx)(λw.zw))v 1β (λx.(λw.zw)x)v 1β (λw.zw)v 1η zv
There is at least one sequence of contractions from the initial term to
the ﬁnal term. Thus, in the formal theory of λ-calculus, the term
(λx.(λy.yx)(λw.zw))v is declared to be equal to zv.
Now, some natural questions arise:
1 Are the sequences themselves normal?
2 What are the non-normal sequences?
3 How are the latter to be identiﬁed and (possibly) normalised?

Brouwer–Heyting–Kolmogorov Interpretation
Proofs rather than truth-values
a proof of the proposition: is given by:
A ∧ B a proof of A and
a proof of B
A ∨ B a proof of A or
a proof of B
A → B a function that turns a proof of A
into a proof of B
∀x.P(x) a function that turns an element a
into a proof of P(a)
∃x.P(x) an element a (witness)
and a proof of P(a)

What is a proof of an equality statement?
t1 = t2 ?
(Perhaps a path from t1 to t2?)
What is the logical status of the symbol “=”?
What would be a canonical/direct proof of t1 = t2?
What is an equality between paths?
What is an equality between homotopies (i.e., paths between
paths)?

Type Theory and Equality
Proposition vs Judgements
In type theory, two main kinds of judgements:
1 x : A
2 x = y : A
Via the so-called Curry-Howard interpretation, “x : A” can be read as
“x is a proof of proposition A”.
Also, “x = y : A” can be read as “x and y are (deﬁnitionally) equal
proofs of proposition A”.
What about the judgement of “p is a proof of the statement that x and
y are equal elements of type A”? This is where the so-called Identity
type comes into the picture:
p : IdA(x, y)

Type Theory and its Derivations-as-Terms
Interpretation
Howard on Curry-Howard
“ [de Bruijn] discovered the idea of derivations as
terms, and the accompanying idea of
formulae-as-types, on his own. (...)
Martin-L¨of suggested that the derivations-as-terms
idea would work particularly well in connection with
Prawitz’s theory of natural deduction.” (W.Howard,
Wadler’s Blog, 2014)

What is the formal counterpart of a proof of an equality?
In talking about proofs of an equality statement, two dichotomies
arise:
1 deﬁnitional equality versus propositional equality
2 intensional equality versus extensional equality
First step on the formalisation of proofs of equality statements: Per
Martin-L¨of’s Intuitionistic Type Theory (Log Coll ’73, published 1975)
with the so-called Identity Type

Identity Types
Identity Types - Topological and Categorical Structure
Workshop, Uppsala, November 13–14, 2006: “The identity type, the
type of proof objects for the fundamental propositional equality, is one
of the most intriguing constructions of intensional dependent type
theory (also known as Martin-L¨of type theory). Its complexity became
apparent with the Hofmann–Streicher groupoid model of type theory.
This model also hinted at some possible connections between type
theory and homotopy theory and higher categories. Exploration of
this connection is intended to be the main theme of the workshop.”
Michael Shulman’s (2017) ‘Homotopy type theory: the logic of
space’: “For many years, the most mysterious part of Martin-L¨of’s
type theory was the identity types “x = y”.”

Identity Types
Type Theory and Homotopy Theory
The groupoid structure exposed in the Hofmann–Streicher (1994)
countermodel to the principle of Uniqueness of Identity Proofs (UIP).
In Hofmann & Streicher’s own words,
“We give a model of intensional Martin-L¨of type theory
based on groupoids and ﬁbrations of groupoids in which
identity types may contain two distinct elements which are
not even propositionally equal. This shows that the principle
of uniqueness of identity proofs is not derivable in the
syntax”. (LICS ’94, pp. 208–212.)

Identity Types
Identity Types as Topological Spaces
According to B. van den Berg and R. Garner (“Topological and
simplicial models of identity types”, ACM Transactions on
Computational Logic, Jan 2012),
“All of this work can be seen as an elaboration of the
following basic idea: that in Martin-L¨of type theory, a type A
is analogous to a topological space; elements a, b ∈ A to
points of that space; and elements of an identity type
p, q ∈ IdA(a, b) to paths or homotopies p, q : a → b in A.”.

Identity Types
Identity Types as Topological Spaces
From the Homotopy type theory collective book (2013):
“In type theory, for every type A there is a (formerly
somewhat mysterious) type IdA of identiﬁcations of two
objects of A; in homotopy type theory, this is just the path
space AI
of all continuous maps I → A from the unit
interval. In this way, a term p : IdA(a, b) represents a path
p : a b in A.”

Identity Types: Iteration
From Propositional to Predicate Logic and Beyond
In the same aforementioned workshop, B. van den Berg in his
contribution “Types as weak omega-categories” draws attention to the
power of the identity type in the iterating types to form a globular set:
“Fix a type X in a context Γ. Define a globular set as follows:
A0 consists of the terms of type X in context Γ,modulo
definitional equality; A1 consists of terms of the types
Id(X; p; q) (in context Γ) for elements p, q in A0, modulo
definitional equality; A2 consists of terms of well-formed
types Id(Id(X; p; q); r; s) (in context Γ) for elements p, q in
A0, r, s in A1, modulo definitional equality; etcetera...”

The homotopy interpretation
Here is how we can see the connections between proofs of equality
and homotopies:
a, b : A
p, q : IdA(a, b)
α, β : IdIdA(a,b)(p, q)
· · · : IdIdId...
(· · · )
Now, consider the following interpretation:
Types Spaces
Terms Maps
a : A Points a : 1 → A
p : IdA(a, b) Paths p : a ⇒ b
α : IdIdA(a,b)(p, q) Homotopies α : p q

The homotopy interpretation (Awodey (2016))
point, path, homotopy, ...

Identity Types
From Vladimir Voevodsky (IAS, Princeton) “Univalent
Foundations: New Foundations of Mathematics”, Mar 26, 2014:
“There were two main problems with the existing
foundational systems which made them inadequate.
Firstly, existing foundations of mathematics were
based on the languages of Predicate Logic and
languages of this class are too limited.
Secondly, existing foundations could not be used to
directly express statements about such objects as, for
example, the ones that my work on 2-theories was
about.”

The Homotopy Interpretation
Steve Awodey (2016)
“The homotopy interpretation was ﬁrst proposed by the present
author and worked out formally (with a student) in terms of Quillen
model categories – a modern, axiomatic setting for abstract
homotopy theory that encompasses not only the classical homotopy
theory of spaces and their combinatorial models like simplicial sets,
but also other, more exotic notions of homotopy (...). The
interpretation was shown to be complete in the logical sense by
Gambino and Garner. These results show that intensional type
theory can in a certain sense be regarded as a “logic of homotopy”, in
that the system can be faithfully represented homotopically, and then
used to reason formally about spaces, continuous maps, homotopies,
and so on. The next thing one might ask is, how much general homo-
topy theory can be expressed in this way? ”
(A proposition is the (homotopy) type of its proofs, Jan 2016.)

Propositional Equality
Proofs of equality as (rewriting) computational paths
What is a proof of an equality statement? In what sense it can be
seen as a homotopy? Motivated by looking at equalities in type
theory as arising from the existence of computational paths between
two formal objects, it may be useful to review the role and the power
of the notion of propositional equality as formalised in the so-called
Curry–Howard functional interpretation.
The main idea, namely, proofs of equality statements as (reversible)
sequences of rewrites, i.e. paths, goes back to a paper entitled
“Equality in labelled deductive systems and the functional
interpretation of propositional equality”, presented in Dec 1993 at the
9th Amsterdam Colloquium, and published in the proceedings in
1994.

Proofs rather than truth-values
A ∧ B a proof of A and
a proof of B
A ∨ B a proof of A or
a proof of B
A → B a function that turns a proof of A
into a proof of B
∀xD
.P(x) a function that turns an element a
into a proof of P(a)
∃xD
.P(x) an element a (witness)
and a proof of P(a)

Brouwer–Heyting–Kolmogorov Interpretation: Formally
Canonical proofs rather than truth-values
a proof of the proposition: has the canonical form of:
A ∧ B p, q where p is a proof of A and
q is a proof of B
A ∨ B inl(p) where p is a proof of A or
inr(q) where q is a proof of B
(‘inl’ and ‘inr’ abbreviate
‘into the left/right disjunct’)
A → B λx.b(x) where b(p) is a proof of B
provided p is a proof of A
∀xD
.P(x) Λx.f(x) where f(a) is a proof of P(a)
provided a is an arbitrary individual chosen
from the domain D
∃xD
.P(x) f(a), a where a is a witness
from the domain D, f(a) is a proof of P(a)

BHK for Identity Types
Types and Propositions
(source: Awodey (2016))
types vs propositions:
sum/coproduct vs disjunction,
product vs conjunction,
function space vs implication
dependent sum vs existential quantiﬁer,
dependent product vs universal quantiﬁer
what happens with equality statements?

t1 = t2 ?
(Perhaps a sequence of rewrites
starting from t1 and ending in t2?)
What is the logical status of the symbol “=”?
What would be a canonical/direct proof of t1 = t2?

Sequences of contractions
(λx.(λy.yx)(λw.zw))v 1η (λx.(λy.yx)z)v 1β (λy.yv)z 1β zv
(λx.(λy.yx)(λw.zw))v 1β (λx.(λw.zw)x)v 1η (λx.zx)v 1β zv
(λx.(λy.yx)(λw.zw))v 1β (λx.(λw.zw)x)v 1β (λw.zw)v 1η zv
There is at least one sequence of contractions from the initial term to
the ﬁnal term. (In this case we have given three!) Thus, in the formal
theory of λ-calculus, the term (λx.(λy.yx)(λw.zw))v is declared to be
equal to zv.
Now, some natural questions arise:
1 Are the sequences themselves normal?
2 Are there non-normal sequences?
3 If yes, how are the latter to be identiﬁed and (possibly)
normalised?
4 What happens if general rules of equality are involved?

Propositional equality
P is β-equal or β-convertible to Q (notation P =β Q) iff Q is
obtained from P by a ﬁnite (perhaps empty) series of
β-contractions and reversed β-contractions and changes of
bound variables. That is, P =β Q iff there exist P0, . . . , Pn
(n ≥ 0) such that
P0 ≡ P, Pn ≡ Q,
(∀i ≤ n − 1)(Pi 1β Pi+1 or Pi+1 1β Pi or Pi ≡α Pi+1).
NB: equality with an existential force.
NB: equality as the reﬂexive, symmetric and transitive closure
of 1-step contraction: arising from rewriting

The Functional Interpretation of Direct Computation
Equality: Existential Force and Rewriting Path
The same happens with λβη-equality:
Deﬁnition 7.5 (λβη-equality) (Hindley & Seldin 2008)
The equality-relation determined by the theory λβη is
called =βη; that is, we deﬁne
M =βη N ⇔ λβη M = N.
Note again that two terms are λβη-equal if there exists a proof
of their equality in the theory of λβη-equality.

Gentzen’s ND for propositional equality
Remark
In setting up a set of Gentzen’s ND-style rules for equality we
need to account for:
1 definitional versus propositional equality;
2 there may be more than one normal proof of a certain
equality statement;
3 given a (possibly non-normal) proof, the process of
bringing it to a normal form should be finite and confluent.

Equality in Type Theory
Martin-Löf’s Intuitionistic Type Theory:
Intensional (1975)
Extensional (1982(?), 1984)
Remark (Definitional vs. Propositional Equality)
definitional, i.e. those equalities that are given as rewrite
rules, orelse originate from general functional principles
(e.g. β, η, ξ, µ, ν, etc.);
propositional, i.e. the equalities that are supported (or
otherwise) by an evidence (a sequence of substitutions
and/or rewrites)

Deﬁnitional Equality
(α) λx.M = λy.[y/x]M (y /∈ FV(M))
(β) (λx.M)N = [N/x]M
(η) (λx.Mx) = M (x /∈ FV(M))
(ξ)
M = M
λx.M = λx.M
(µ)
M = M
NM = NM
(ν)
M = M
MN = M N
(ρ) M = M
(σ)
M = N
N = M
(τ)
M = N N = P
M = P

Intuitionistic Type Theory
→-intro
[x : A]
f(x) = g(x) : B
λx.f(x) = λx.g(x) : A → B
(ξ)
→-elim
x = y : A g : A → B
gx = gy : B
(µ)
→-elim
x : A g = h : A → B
gx = hx : B
(ν)
→-reduc
a : A
[x : A]
b(x) : B
(λx.b(x))a = b(a/x) : B
(β)
c : A → B
λx.cx = c : A → B
(η)

The Functional Interpretation of Direct Computations
Lessons from Curry–Howard and Type Theory
Harmonious combination of logic and λ-calculus;
Proof terms as ‘record of deduction steps’, i.e.
‘deductions-as-terms’
Function symbols as ﬁrst class citizens.
Cp.
∃xF(x)
[F(t)]
C
C
with
p : ∃xF(x)
[t : D, g(t) : F(t)]
h(g, t) : C
? : C
in the term ‘?’ the variable g gets abstracted from, and this enforces a
kind of generality to g, even if this is not brought to the ‘logical’ level.

Equality in Martin-L¨of’s Intensional Type Theory
A type a : A b : A
Idint
A (a, b) type
Idint
-formation
a : A
r(a) : Idint
A (a, a)
Idint
-introduction
a = b : A
r(a) : Idint
A (a, b)
Idint
-introduction
a : A b : A c : Idint
A (a, b)
[x:A]
d(x):C(x,x,r(x))
[x:A,y:A,z:Idint
A (x,y)]
C(x,y,z) type
J(c, d) : C(a, b, c)
Idint
-elimination
a : A
[x : A]
d(x) : C(x, x, r(x))
[x : A, y : A, z : Idint
A (x, y)]
C(x, y, z) type
J(r(a), d(x)) = d(a/x) : C(a, a, r(a))
Idint
-equality

Equality in Martin-L¨of’s Extensional Type Theory
A type a : A b : A
Idext
A (a, b) type
Idext
-formation
a = b : A
r : Idext
A (a, b)
Idext
-introduction
c : Idext
A (a, b)
a = b : A
Idext
-elimination
c : Idext
A (a, b)
c = r : Idext
A (a, b)
Idext
-equality

The missing entity
Considering the lessons learned from Type Theory, the
judgement of the form:
a = b : A
which says that a and b are equal elements from domain D, let
us add a function symbol:
a =s b : A
where one is to read: a is equal to b because of ‘s’ (‘s’ being
the rewrite reason); ‘s’ is a term denoting a sequence of
equality identiﬁers (β, η, ξ, etc.), i.e. a composition of rewrites.
In other words, ‘s’ is the computational path from a to b.
(This formal entity is missing in both of Martin-L¨of’s
formulations of Identity Types.)

HoTT Book
Encode-Decode Method
“To characterize a path space, the first step is to
define a comparison fibration “code” that provides a
more explicit description of the paths.”
(...)
“There are several different methods for proving that
such a comparison fibration is equivalent to the paths
(we show a few different proofs of the same result in
§8.1). The one we have used here is called the
encode-decode method.”

Propositional Equality
Id-introduction
a =s b : A
s(a, b) : IdA(a, b)
Id-elimination
m : IdA(a, b)
[a =g b : A]
h(g) : C
J(m, λg.h(g)) : C
Id-reduction
a =s b : A
s(a, b) : IdA(a, b)
Id-intr
[a =g b : A]
h(g) : C
J(s(a, b), λg.h(g)) : C
Id-elim
β
[a =s b : A]
h(s/g) : C

Propositional Equality: A Simple Example of a Proof
By way of example, let us prove
ΠxA
ΠyA
(IdA(x, y) → IdA(y, x))
[p : IdA(x, y)]
[x =t y : A]
y =σ(t) x : A
(σ(t))(y, x) : IdA(y, x)
J(p, λt(σ(t))(y, x)) : IdA(y, x)
λp.J(p, λt(σ(t))(y, x)) : IdA(x, y) → IdA(y, x)
λy.λp.J(p, λt(σ(t))(y, x)) : ΠyA(IdA(x, y) → IdA(y, x))
λx.λy.λp.J(p, λt(σ(t))(y, x)) : ΠxAΠyA(IdA(x, y) → IdA(y, x))

Propositional Equality: The Groupoid Laws
With the formulation of propositional equality that we have just
deﬁned, we can also prove that all elements of an identity type
obey the groupoid laws, namely
1 Associativity
2 Existence of an identity element
3 Existence of inverses
Also, the groupoid operation, i.e. composition of
paths/sequences, is actually, partial, meaning that not all
elements will be connected via a path. (The groupoid
interpretation refutes the Uniqueness of Identity Proofs.)

Propositional Equality: The Uniqueness of Identity Proofs
“We will call UIP (Uniqueness of Identity Proofs) the following
property. If a1, a2 are objects of type A then for any proofs p
and q of the proposition “a1 equals a2” there is another proof
establishing equality of p and q. (...) Notice that in traditional
logical formalism a principle like UIP cannot even be
sensibly expressed as proofs cannot be referred to by
terms of the object language and thus are not within the
scope of propositional equality.” (Hofmann & Streicher 1996)

Normal form for the rewrite reasons
Strategy:
Analyse possibilities of redundancy
Construct a rewriting system
Prove termination and conﬂuence

Definition (equation)
An equation in our LNDEQ is of the form:
s =r t : A
where s and t are terms, r is the identifier for the rewrite reason, and
A is the type (formula).
Definition (system of equations)
A system of equations S is a set of equations:
{s1 =r1
t1 : A1, . . . , sn =rn
tn : An}
where ri is the rewrite reason identifier for the ith equation in S.

Deﬁnition (rewrite reason)
Given a system of equations S and an equation s =r t : A, if
S s =r t : A, i.e. there is a deduction/computation of the
equation starting from the equations in S, then the rewrite
reason r is built up from:
(i) the constants for rewrite reasons: { ρ, σ, τ, β, η, ν, ξ, µ };
(ii) the ri’s;
using the substitution operations:
(iii) subL;
(iv) subR;
and the operations for building new rewrite reasons:
(v) σ, τ, ξ, µ.

Definition (general rules of equality)
The general rules for equality (reflexivity, symmetry and
transitivity) are defined as follows:
x : A
x =ρ x : A
(reflexivity)
x =t y : A
y =σ(t) x : A
(symmetry)
x =t y : A y =u z : A
x =τ(t,u) z : A
(transitivity)

Deﬁnition (subterm substitution)
The rule of “subterm substitution” is split into two rules:
x =r C[y] : A y =s u : A
x =subL(r,s) C[u] : A
x =r w : A C[w] =s u : A
C[x] =subR(r,s) u : A
where C[x] is the context in which the subterm x appears

Reductions
Deﬁnition (reductions involving ρ and σ)
x =ρ x : A
x =σ(ρ) x : A
sr x =ρ x : A
x =r y : A
y =σ(r) x : A
x =σ(σ(r)) y : A
ss x =r y : A
Associated rewritings:
σ(ρ) sr ρ
σ(σ(r)) ss r

Reductions
Deﬁnition (reductions involving τ)
x=r y:D y=σ(r)x:D
x=τ(r,σ(r))x:D tr x =ρ x : D
y=σ(r)x:D x=r y:D
y=τ(σ(r),r)y:D tsr y =ρ y : D
u=r v:D v=ρv:D
u=τ(r,ρ)v:D rrr u =r v : D
u=ρu:D u=r v:D
u=τ(ρ,r)v:D lrr u =r v : D
Associated equations: τ(r, σ(r)) tr ρ, τ(σ(r), r) tsr ρ, τ(r, ρ) rrr r,
τ(ρ, r) lrr r.

Reductions
Deﬁnition
βrewr -×-reduction
x =r y : A z : B
x, z =ξ1(r) y, z : A × B
× -intr
FST( x, z ) =µ1(ξ1(r)) FST( y, z ) : A
× -elim
mx2l1 x =r y : A
Associated rewriting:
µ1(ξ1(r)) mx2l1 r

Reductions
Deﬁnition
βrewr -×-reduction
x =r x : A y =s z : B
x, y =ξ∧(r,s) x , z : A × B
× -intr
FST( x, y ) =µ1(ξ∧(r,s)) FST( x , z ) : A
× -elim
mx2l2 x =r x : A
Associated rewriting:
µ1(ξ∧(r, s)) mx2l2 r

Categorical Interpretation of Computational Paths
Computational Paths form a Weak Category
Theorem
For each type A, computational paths induce a weak
categorical structure Arw where:
objects: terms a of the type A, i.e., a : A
morphisms: a morphism (arrow) between terms a : A and
b : A are arrows s : a → b such that s is a computational
path between the terms, i.e., a =s b : A.
Corollary
Arw has a weak groupoidal structure.

Publications
Recent publications:
1 R. J. G. B. de Queiroz, A. G. de Oliveira and A. F. Ramos.
Propositional equality, identity types, and direct computational
types. Special issue of South American Journal of Formal Logic
(ISSN: 2446-6719) entitled “Logic and Applications: in honor to
Francisco Miraglia by the occasion of his 70th birthday”, M.
Coniglio & H. L. Mariano (eds.), 2(2):245–296, December 2016.
2 A. F. Ramos, R. J. G. B. de Queiroz, A. G. de Oliveira. On The
Identity Type as The Type of Computational Paths. EBL’14
special issue of Logic Journal of the IGPL, Oxford Univ Press,
Published online 26 June 2017.
3 A. F. Ramos, R. J. G. B. de Queiroz, A. G. de Oliveira. On the
Groupoid Model of Computational Paths. arXiv:1506.02721

Propositional equality, identity types, and computational paths

More Related Content

What's hot

Similar to Propositional equality, identity types, and computational paths

More from Ruy De Queiroz

Recently uploaded

Propositional equality, identity types, and computational paths