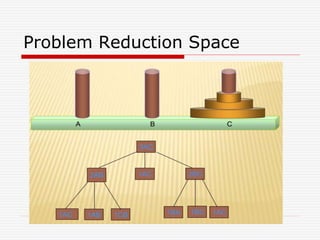
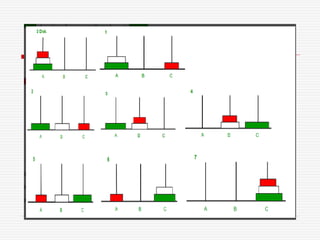
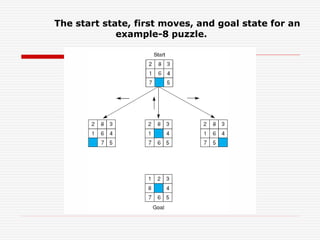
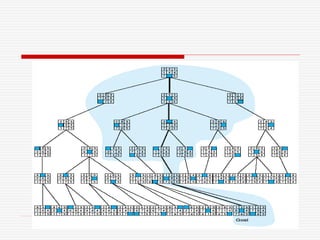
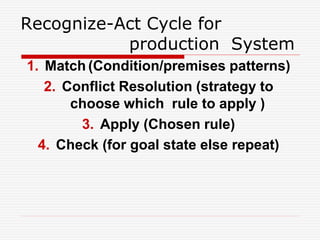
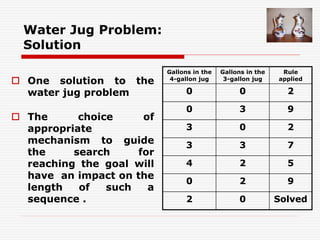
The document outlines the process of defining, analyzing, and solving problems in the context of AI systems, emphasizing the importance of state space representation and problem reduction. It discusses the production systems which consist of rules, knowledge databases, and control strategies to systematically derive solutions to problems like the Water Jug problem. Notably, it addresses advantages and disadvantages of production systems, including issues like opacity and inefficiency, while demonstrating problem-solving techniques through examples.

1. Problems, Problem
Spaces and Search

2. Requirements for solving a problem
To build a system to solve a problem,
four things are required:
• Define the problem precisely.
• Analyze the problem.
• Isolate and represent the task knowledge
that is necessary to solve the problem.
• Choose the best problem-solving
techniques and apply them to the
particular problem.

3. Defining the problem as
a State Space Search
The state space representation forms the root of most of the AI methods.
 Its structure corresponds to the structure of problem solving in
two important ways:
 to convert some given situation into some desired
situation using a set of permissible operations.
 to define the process of solving a particular problem as
a combination of known techniques (each represented
as a rule defining a single step in the space) and
search.
 Search is the general technique of exploring the
space to try to find some path from current state to a
goal state.
 Search is a very important process in the solution of
hard problems for which no more direct techniques
are available.

4.  World State or simply State: values of all attributes of
interest in the world.
 State Space: the set of all possible world states.
 Initial State: The values of attributes that are in effect at
the beginning of a problem.
 Goal: A world state or set of states to be reached as a result
of a search.
Defining the problem as
a State Space Search

5. Problem Reduction(State Space for 3
Disk Tower of Hanoi Problem

6. State Space
 The states represent situations of the problem.
 The operators represent actions in the world.
 forward search: the root of the problem space
represents the start state, and the search proceeds
forward to a goal state.
 backward search : the root of the problem space
represents the goal state, and the search proceeds
backward to the initial state.

7. Problem Reduction Space
 The root node, labeled “3AC” represents the
original problem of transferring all 3 disks from
peg A to peg C.
 The goal can be decomposed into three
subgoals: 2AB, 1AC, 2BC. In order to achieve
the goal, all 3 subgoals must be achieved.

8. Problem Reduction Space

10. Problem Reduction Space
 In a problem reduction space, the
nodes represent problems to be
solved or goals to be achieved, and
the edges represent the
decomposition of the problem into
subproblems.
 This is best illustrated by the
example of the Towers of Hanoi
problem.

11.  The Same approach can be applied
for 8-Puzzle problem

12. The start state, first moves, and goal state for an
example-8 puzzle.

14. Production Systems
A production system consists of:
 Set of rules: which are of the form P  Q, where left side
represents the current problem state and right side
represents a result or generated output state.
 Knowledge/Databases: contain whatever information is
appropriate for the particular task. Some parts of the
database may be permanent, while other parts of it may
pertain only to the solution of the current problem.
 Control strategy: rules will be compared to the database
and a way of resolving the conflicts that arise when several
rules match at once.
 Rule applier: checks the applicability of the rule by
matching the current state with the left hand side of the
rule and finds appropriate rule from the database of rules.

15. Control Strategies or
Search Strategies
 Adopted for applying the rules and searching the problem
solution in search space.
 If, wrong control strategy is applied, it may be possible
that a solution is never obtained.
 The two requirements of a good control strategy are:
 It should cause motion.
 Movement of the problem should be in the direction of
obtaining the solution.
 It should be systematic.
 There should be a systematic method to select a rule
for application.

16. Production System
Rules
• Production rules can be categorized as Deductive inference rules
• We can represent knowledge in a production system as a set of
rules of the form
– If (condition) THEN (condition)
along with a control system and a database.
• The production rules are also known as condition – action,
antecedent –consequent, pattern – action, situation – response,
feedback – result pairs.
For example,
If (you have an exam tomorrow) THEN (study the whole night)

17. Recognize-Act Cycle for
production System
1. Match (Condition/premises patterns)
2. Conflict Resolution (strategy to
choose which rule to apply )
3. Apply (Chosen rule)
4. Check (for goal state else repeat)

18. Features of Production System
• Some of the main features of production system are:
• Expressiveness and intuitiveness: In real world, many times situation comes like “if this happen-
you will do that”, “if this is so-then this should happen” and many more. The production rules
essentially tell us what to do in a given situation.
a. Simplicity: The structure of each sentence in a production system is unique and uniform as
they use “IF-THEN” structure. This structure provides simplicity in knowledge
representation. This feature of production system improves the readability of production
rules.
b. Modularity: This means production rule code the knowledge available in discrete pieces.
Information can be treated as a collection of independent facts which may be added or
deleted from the system with essentially no deleterious side effects.
c. Modifiability: This means the facility of modifying rules. It allows the development of
production rules in a skeletal form first and then it is accurate to suit a specific application.
d. Knowledge intensive: The knowledge base of production system stores pure knowledge. This
part does not contain any type of control or programming information. Each production
rule is normally written as an English sentence; the problem of semantics is solved by the
very structure of the representation.

19. Advantages of production systems
1.Production systems provide an excellent tool for
structuring AI programs.
2.Production Systems are highly modular because
the individual rules can be added, removed or
modified independently.
3.The production rules are expressed in a natural
form, so the statements contained in
 the knowledge base should the a recording of an
expert thinking out loud.

20. Disadvantages of production
system
1.Opacity: This problem is generated by the combination of production rules. The opacity is generated
because of less prioritization of rules. More priority to a rule has the less opacity.
2.Inefficiency: During execution of a program several rules may active. A well devised control strategy
reduces this problem. As the rules of the production system are large in number and they are hardly
written in hierarchical manner, it requires some forms of complex search through all the production
rules for each cycle of control program.
3.Absence of learning: Rule based production systems do not store the result of the problem for future
use. Hence, it does not exhibit any type of learning capabilities. So for each time for a particular
problem, some new solutions may come.
4.Conflict resolution: The rules in a production system should not have any type of conflict operations.
When a new rule is added to a database, it should ensure that it does not have any conflicts with the
existing rules.
5.It may be very difficult analyse the flow of control within a production system because the individual
rules don’t call each other.

21. Water Jug Problem:
Problem Statement
 You are given:
 a tap of running water,
 a 3 Gallon jug
 a 4 Gallon jug
 No measuring marks on either water jug
 The goal: Get 2 gallons of water in the 4 gallon
jug.
 Actions:
 Filling jugs from tap
 dumping water in jugs onto ground
 dumping 4 gallon into 3 gallon jug until 3 gallon jug
is full
 Dumping 3 gallon jug into 4 gallon jug until empty or
until 4 gallon is full, etc, etc.
How will you solve this problem?

22. Water Jug Problem:
Problem Statement
 State space:- set of ordered pairs of integers (x,y)
such that
x = 0, 1,2, 3 or 4 and
y = 0,1,2 or 3;
x represents the number of gallons of water in
the 4-gallon jug and
y represents the quantity of water in 3-gallon jug.
 The initial state is (0,0)
 The goal state is (2,n)

23. Water Jug Problem:
Production rules
S.No Current state/condition Next State Description
1 (x,y)/ if x < 4 (4,y) Fill the 4 gallon jug
2 (x,y)/ if y <3 (x,3) Fill the 3 gallon jug
3 (x,y)/ if x > 0 (x-d, y) Pour some water out of the 4
gallon jug
4 (x,y)/ if y > 0 (x, y-d) Pour some water out of the 3-
gallon jug
5 (x,y)/ if x > 0 (0, y) Empty the 4 gallon jug
6 (x,y)/ if y > 0 (x, 0) Empty the 3 gallon jug on the
ground
7 (x,y)/ if x+y >= 4
and y >0
(4, y-(4-x)) Pour water from the 3 –gallon
jug into the 4 –gallon jug until
the 4-gallon jug is full

24. Water Jug Problem:
Production rules
S.No Current state/condition Next State Description
8 (x, y)/ if x+y >= 3 and
x>0
(x-(3-y), 3) Pour water from the 4-
gallon jug into the 3-gallon
jug until the 3-gallon jug is
full
9 (x, y)/ if x+y <=4 and
y>0
(x+y, 0) Pour all the water from the
3-gallon jug into the 4-
gallon jug
10 (x, y)/ if x+y <= 3 and
x>0
(0, x+y) Pour all the water from the
4-gallon jug into the 3-
gallon jug

25. Production Rules:
How to apply
 Required:
 A set of rules
 Each rule must have a left side and a right side
and must cause a change from the current state to
the next state while moving nearer to the goal
 A control structure
 Process:
 The control structure loops through a simple
cycle:
Step 1:Check the state of the left side of the current rule
Step 2:If it is the current state, execute the right side of the
rule to change the state to the next state
Step 3:Is the next state a goal state?
Step 3a:If yes, the problem is solved.
Step 3b:Otherwise, go to the next rule.
Step 4:Go to step 1 and repeat the cycle.

26. Water Jug Problem:
Solution
 One solution to the
water jug problem
 The choice of
appropriate
mechanism to guide
the search for
reaching the goal will
have an impact on the
length of such a
sequence .
Gallons in the
4-gallon jug
Gallons in the
3-gallon jug
Rule
applied
0 0 2
0 3 9
3 0 2
3 3 7
4 2 5
0 2 9
2 0 Solved