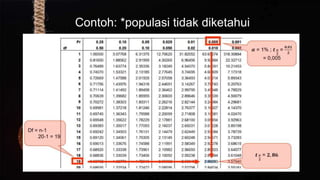
Dokumen ini membahas teori pendugaan dalam statistik, termasuk pendugaan titik dan interval, serta metode pengujian hipotesis. Pendugaan titik memberikan satu nilai untuk menduga parameter populasi, sedangkan pendugaan interval mencakup selang di mana parameter tersebut mungkin berada. Beberapa contoh dihitung untuk menunjukkan penerapan rumus dalam konteks populasi yang diketahui dan tidak diketahui.

1. Probabilitas
dan Statistika
Milasari, S.Pd., M.Pd

2. Pertemuan ke 9

3. Pembahasan
Teori Pendugaan:
 Pendugaan Titik
 Pendugaan Interval
 Metode Pendugaan
 Selang Kepercayaan

4. Teori Pendugaan

5. Definisi
Teori pendugaan merupakan suatu proses dengan
menggunakan statistik sampel untuk menduga parameter
populasi.
Jadi, jika sampel adalah wilayah kecil dan populasi adalah
wilayah yang besar, maka parameter populasi merupakan
ukuran daripada populasi dimana kita memetakan ukuran dari
populasi dengan menggunakan sampel
Pengujian hipotesis
Merupakan suatu proses yang memutuskan apakah hasil
dugaan tersebut diterima atau ditolak

6. Pendugaan Titik Parameter Populasi
Pendugaan titik parameter populasi adalah suatu pendugaan
yang terdiri dari satu nilai saja yang digunakan untuk
menduga parameter.

7. Rumus:
x
̅ = 1/n ∑ xi
s2 = 1/(n-1) ∑(xi - x
̅ )
x
̅ = rata-rata sampel
s2 = standar deviasi sampel
x = data sampel
n = jumlah sampel

8. Pendugaan Interval
Pendugaan interval adalah suatu interval yang menyatakan
selang dimana suatu parameter populasi mungkin berada.
• Suatu dugaan tidak mungkin mencapai 100%
• Interval keyakinan dibatasi oleh 2 nilai yaitu: batas atas dan
batas bawah

9. Pendugaan Interval
(S – Zsx < P < S + Zsx) = C
Keterangan:
P = parameter populasi yang tidak diketahui
C = Probabilitas atau tingkat keyakinan yang ditentukan
terlebih dahulu
S = Statistik yang merupakan parameter penduga populasi (P)
Sx = standar deviasi sampel
(S – Zsx) = batas bawah keyakinan
(S + Zsx) = batas atas keyakinan

10. Interval keyakinan untuk rata-rata
Distribusi normal dan standar deviasi populasi diketahui
(µ ± Za/2 Sx) = C
(-Za/2 Sx < µ < + Za/2 Sx) = C*
Distribusi normal dan standar deviasi populasi tidak diketahui
(µ ± ta/2 Sx) = C
(x
̅ -ta/2 Sx < µ < x
̅ + ta/2 Sx) = C**
*lihat tabel Z, untuk nilai Za/2
**lihat tabek t, untuk nilai ta/2

11. Kesalahan standar dari rata-rata
hitung sampel *populasi diketahui
Untuk populasi tidak terbatas n/N < 0,05
Untuk populasi terbatas n/N > 0,05
Keterangan:
σ = standar deviasi populasi
N = jumlah sampel
Sx = penduga standar deviasi sampel untuk menghitung
interval populasi

12. Contoh: *populasi diketahui
Standar deviasi Return on Asset (ROA) 37 perbankan di
Indonesia adalah 2,35. jika diambil 10 sampel dari 37
perbankan dengan rata-rata ROA adalah 0,43. Buatlah
interval keyakinan dengan tingkat kepercayaan 80%, 90%,
95%!
Diketahui:
σ = 2,35
µ = 0,43
N = 37
n = 10
C = 80%, 90% dan 95%

13. Contoh: *populasi diketahui
Tentukan populasi terbatas atau tidak terbatas
n/N = 10/37 = 0,27 > 0,05
(populasi terbatas)
Rumus interval keyakinan untuk populasi terbatas
(-Za/2 Sx < µ < + Za/2 Sx) = C*

14. Contoh: *populasi diketahui
1. Cari std sampel dengan populasi terbatas

15. Contoh: *populasi diketahui
2. Cari nilai Za/2 dengan nilai C = 80% atau α = 20%
Nilai 0,4
Lihat di tabel Z, untuk menentukan nilai Z

16. Nilai Za/2 = 1,28 (dari tabel Z)

17. Contoh: *populasi diketahui
3. Selesaikan rumus interval keyakinan
(-Za/2 Sx < µ < + Za/2 Sx) = C*
(0,43 – (1,28 x 0,64) < µ < (0,43 + (1,28 x 0,64)
(0,43 – 0,82) < µ < 0,43 + 0,82)
-0,39 < µ < 1,25
Kesimpulan:
Interval Return Asset (ROA) perbankan di
indonesia adalah -0,39% sampai dengan
1,25% per tahun.
Dik:
Za/2 = 1,28
Sx = 0,64
µ = 0,43

18. Tugas!
Buatlah interval keyakinan dengan tingkat
kepercayaan 90% dan 95%!

19. Contoh: *populasi tidak diketahui
Pada tahun 2022, terdapat 677 emiten yang terdaftar di BEI.
20 emiten merupakan saham yang paling diminati investor.
Rata-rata 20 saham ini dapat memberikan return saham
sebesar 15% dengan standar deviasi 1,5%. Buatlah interval
keyakinan dengan tingkat kepercayaan 99%!
Diketahui:
S = 1,5
x
̅ = 15
N = 677
n = 20
C = 99%

20. Contoh: *populasi tidak diketahui
Tentukan populasi terbatas atau tidak terbatas
n/N = 20/677 = 0,02 < 0,05
(populasi tidak terbatas)
Rumus interval keyakinan untuk populasi terbatas
(x
̅ -ta/2 Sx < µ < x
̅ + ta/2 Sx) = C**

21. Contoh: *populasi tidak diketahui
1. Cari std sampel dengan populasi tidak terbatas

22. Contoh: *populasi tidak diketahui

23. Contoh: *populasi tidak diketahui

24. Contoh: *populasi tidak diketahui
3. Selesaikan rumus interval keyakinan
(x̅ -ta/2 Sx < µ < x
̅ + ta/2 Sx) = C**
(15 – (2,86 x 0,34) < µ < (15 + (2,86 x 0,34)
(15 – 0,97) < µ < (15 + 0,97)
(14,03) < µ < (15,97)
Kesimpulan:
Interval Return saham emiten di Indonesia 99% adalah antara
14,03 – 15,97.

25. Thank You