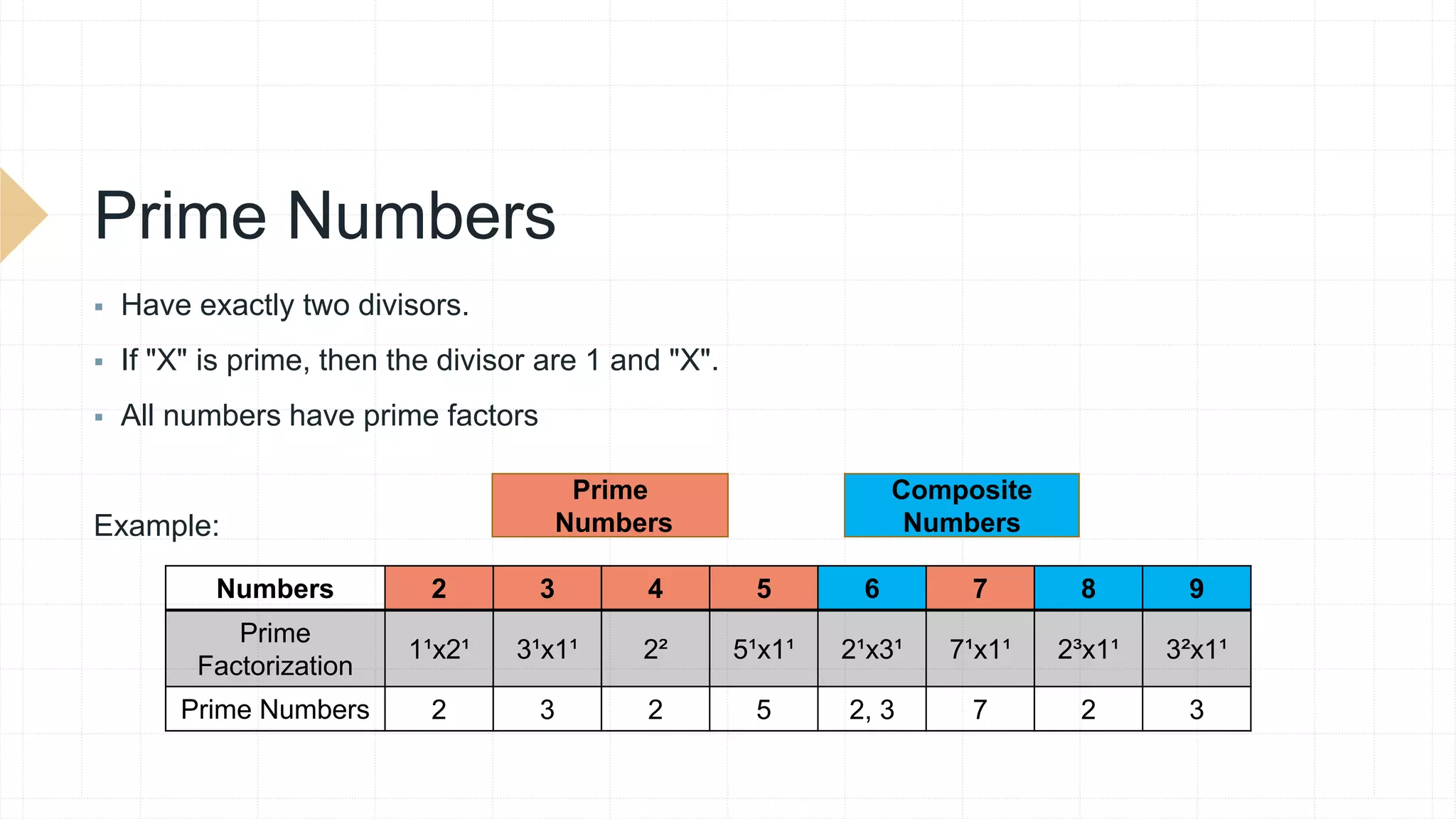
This document discusses prime numbers and their importance in cryptography. It defines prime numbers as numbers greater than 1 that are only divisible by 1 and themselves. Composite numbers are numbers that have more than two factors. The document notes that many encryption algorithms are based on prime numbers because they are fast to multiply but extremely difficult to factor back into primes. It also lists several conjectures regarding prime numbers and outlines learning objectives about understanding primes and their role in cryptography.

1. Prime Numbers,
Cryptography
and Network
Security
José Bermúdez, Ph.D.

2. Cryptography
Alan Turing:
 Born: 23 June 1912 · Maida Vale, London, England
 Died: 7 June 1954 (aged 41) · Wilmslow, Cheshire, England
 Cause of death Cyanide poisoning
Father of Modern Computer.
Father of Artificial Intelligence.
Father of many things.

3. Outcomes:
Upon the completion of this session, the learners will be able to:
 Understand about prime numbers and composite numbers.
 Know some facts about prime numbers.
 Know the role to prime numbers in cryptography.

4. Prime Numbers
 Have exactly two divisors.
 If "X" is prime, then the divisor are 1 and "X".
 All numbers have prime factors
Example:
Numbers 2 3 4 5 6 7 8 9
Prime
Factorization
1¹x2¹ 3¹x1¹ 2² 5¹x1¹ 2¹x3¹ 7¹x1¹ 2³x1¹ 3²x1¹
Prime Numbers 2 3 2 5 2, 3 7 2 3

5. Prime Numbers
 Have exactly two divisors.
 If "X" is prime, then the divisor are 1 and "X".
 All numbers have prime factors
Example:
Numbers 2 3 4 5 6 7 8 9
Prime
Factorization
1¹x2¹ 3¹x1¹ 2² 5¹x1¹ 2¹x3¹ 7¹x1¹ 2³x1¹ 3²x1¹
Prime Numbers 2 3 2 5 2, 3 7 2 3
Prime
Numbers
Composite
Numbers

6. Prime Numbers
 A prime number is a number greater than 1 with only two factors, itself and one.
 It cannot be divided further by any other number without leaving a remainder.

7. Why prime numbers
are important for
cryptography
 Many encryption algorithms are based on
prime numbers.
 Very fast to multiply two large prime numbers.
 Extreme computer-intensive to do the reverse
(found the prime numbers)
 Factoring very large numbers is very hard.
86331288713595159341392743491288713595
1359583051879012887

8. Prime Numbers
Conjectures
 Goldbach's conjecture
 Twin prime conjecture
 Andrica's conjecture,
 Brocard's conjecture,
 Legendre's conjecture,
 Oppermann's conjecture
 Cramér conjecture
 ...

9. Summary:
 Learned about prime numbers and composite numbers.
 Know some facts about prime numbers.
 Know the role to prime numbers in cryptography.

10. Prime Numbers,
Cryptography
and Network
Security
José Bermúdez, Ph.D.