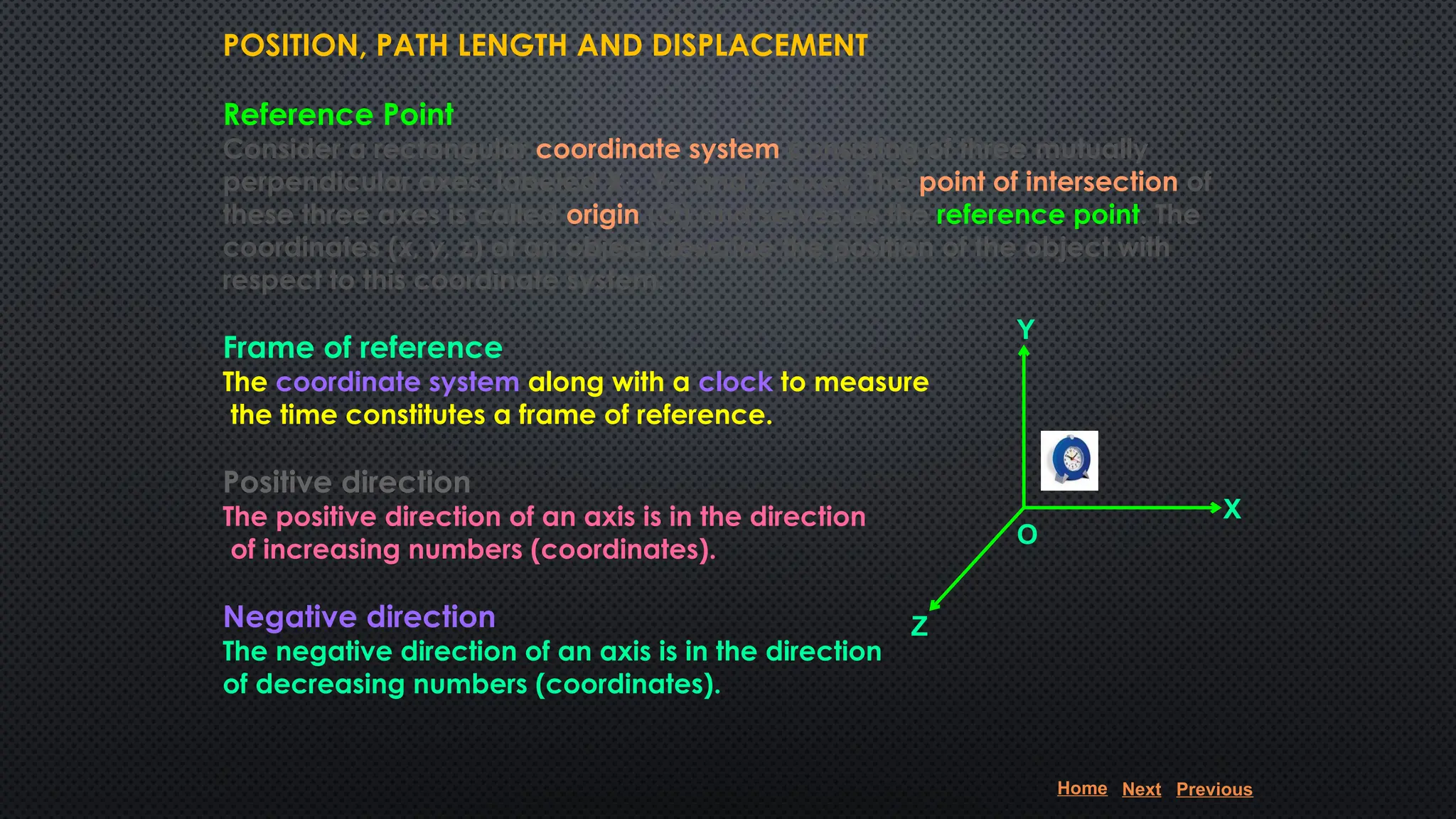
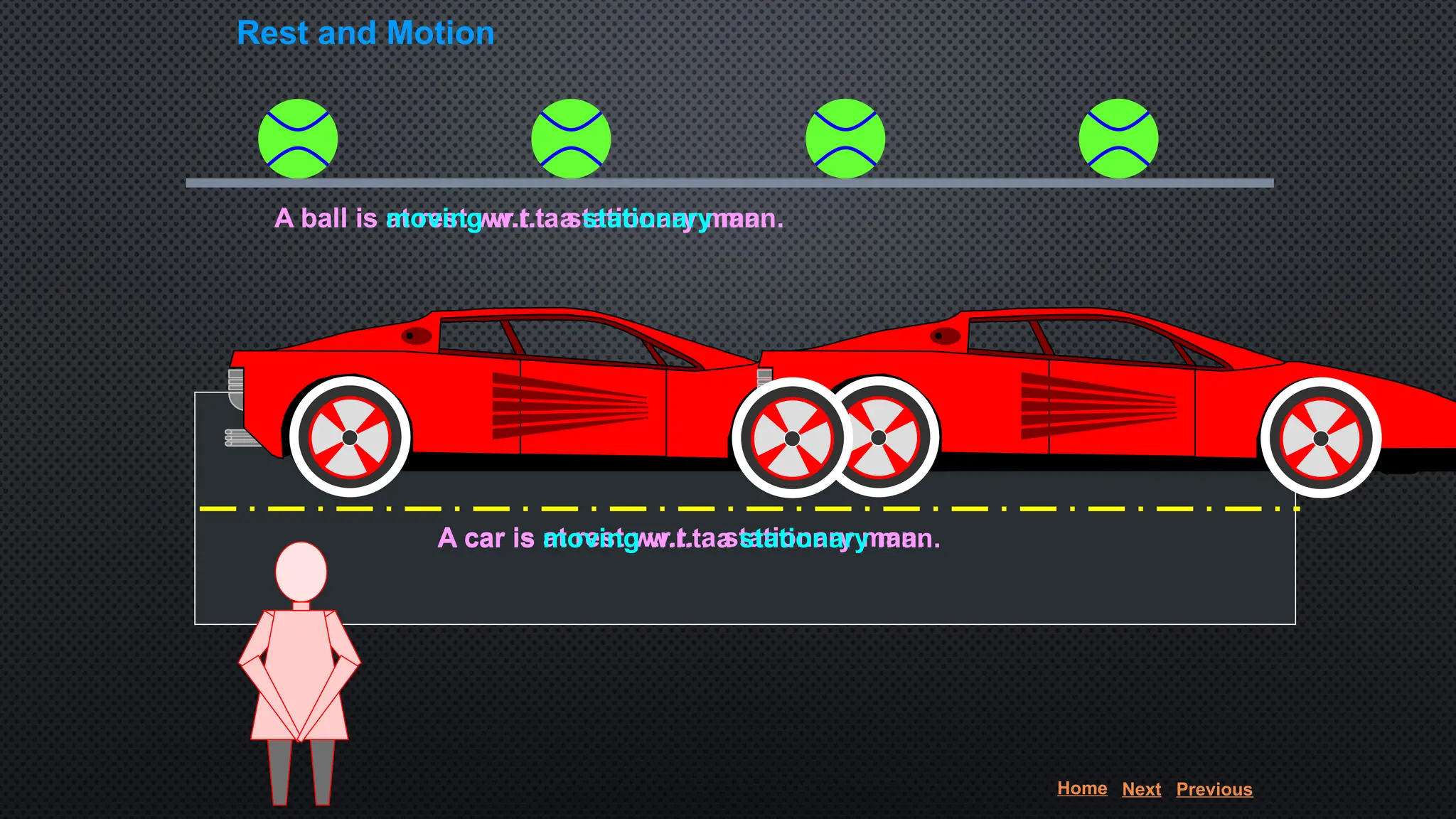
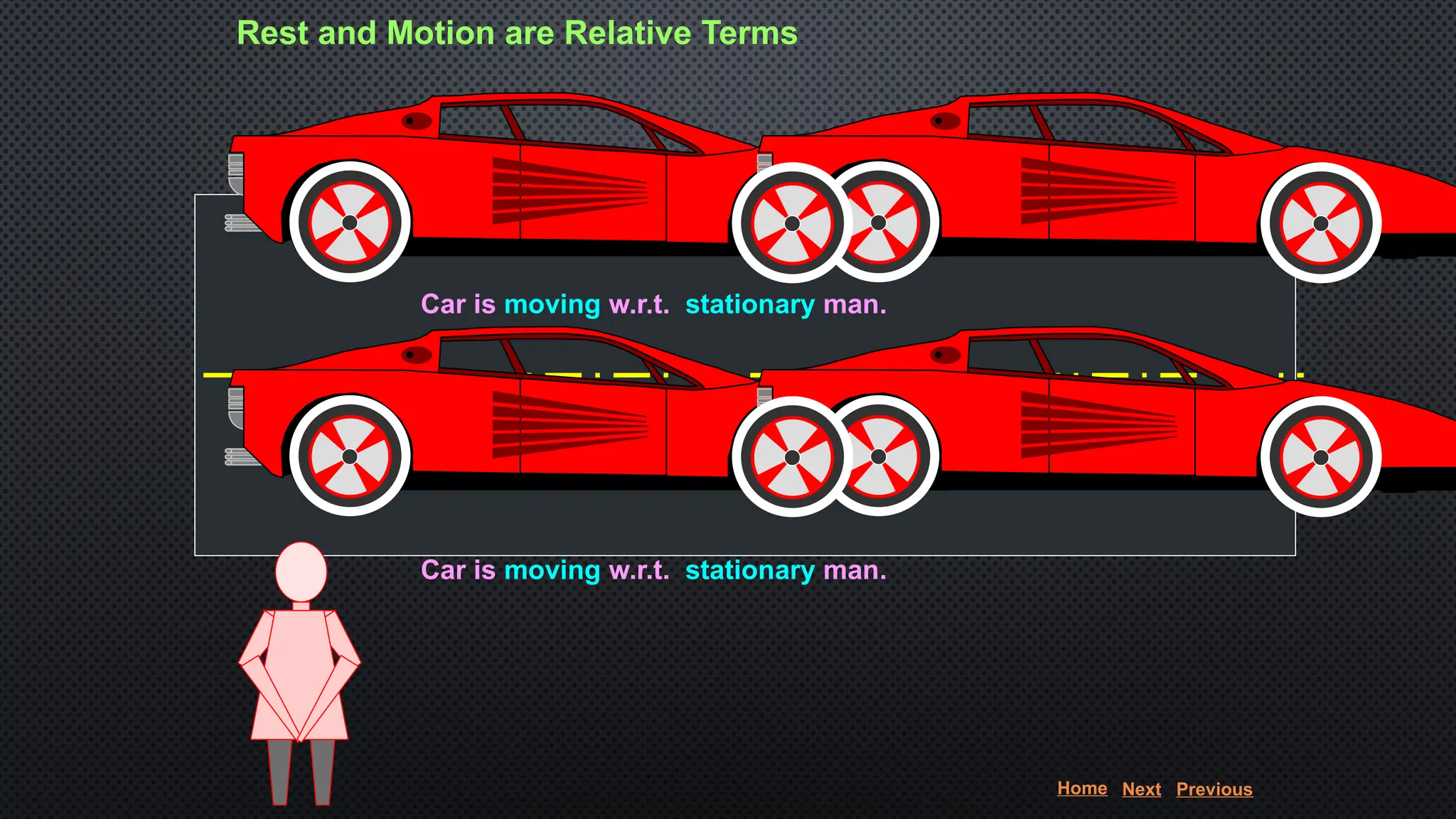
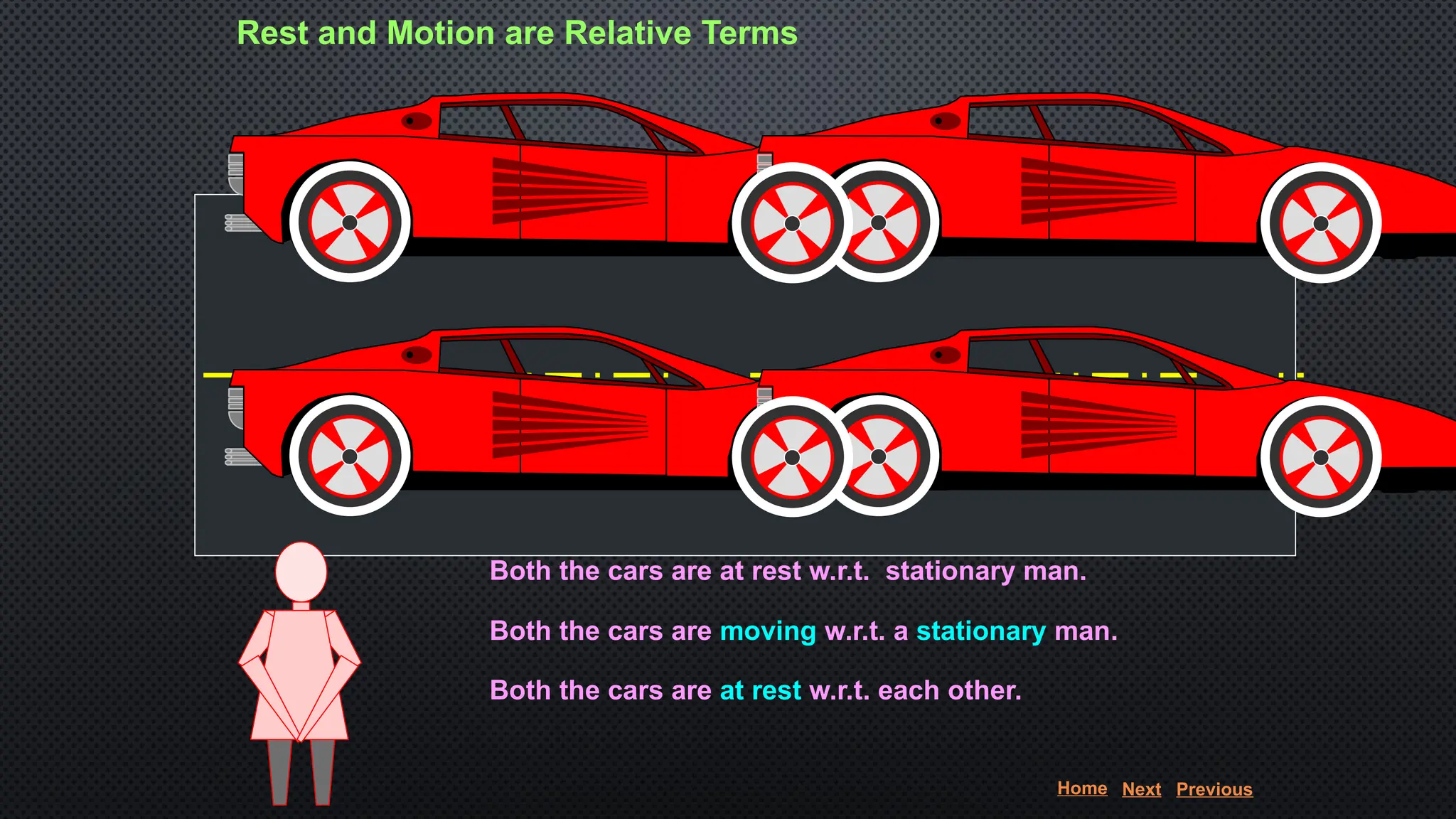
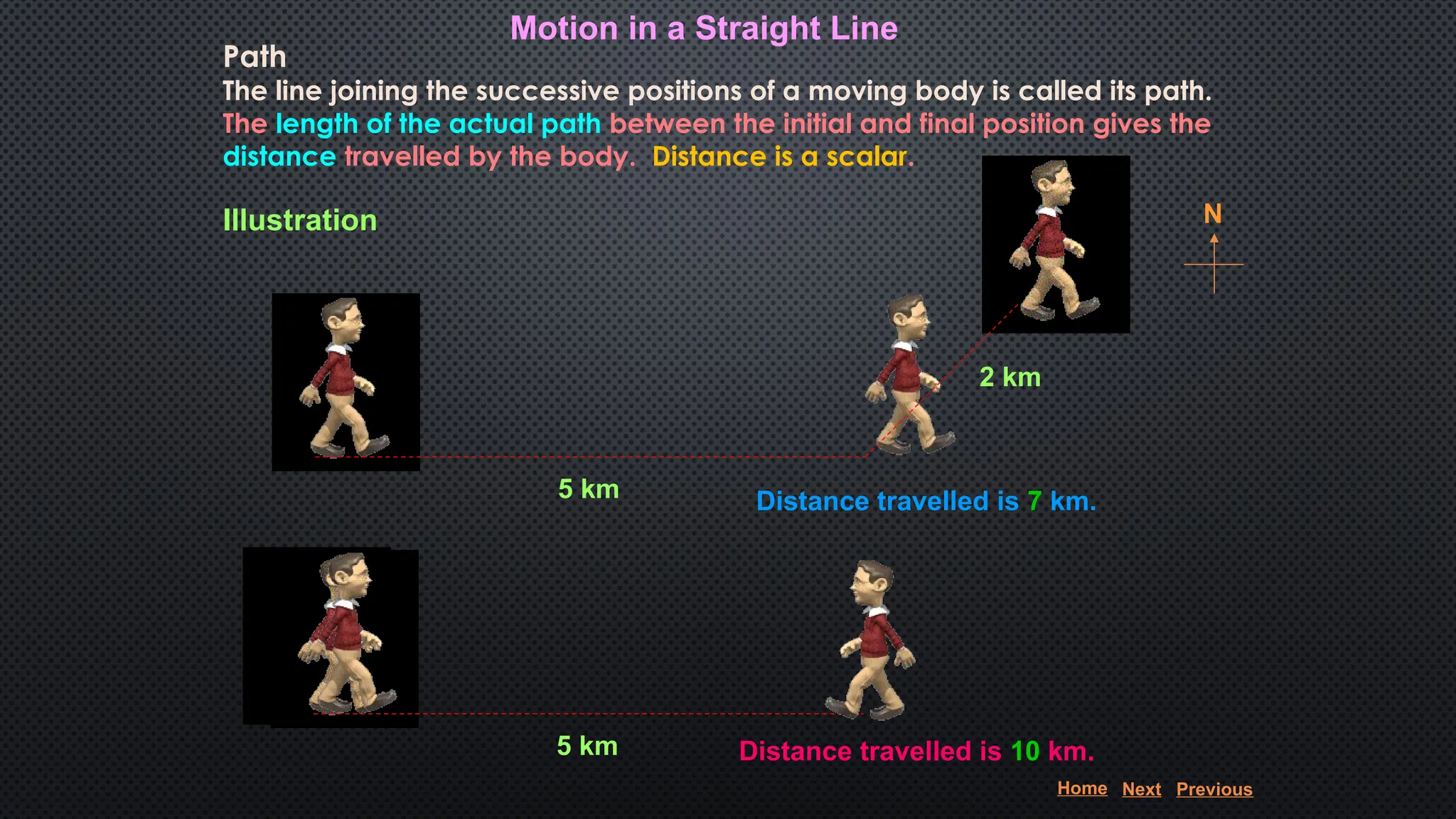
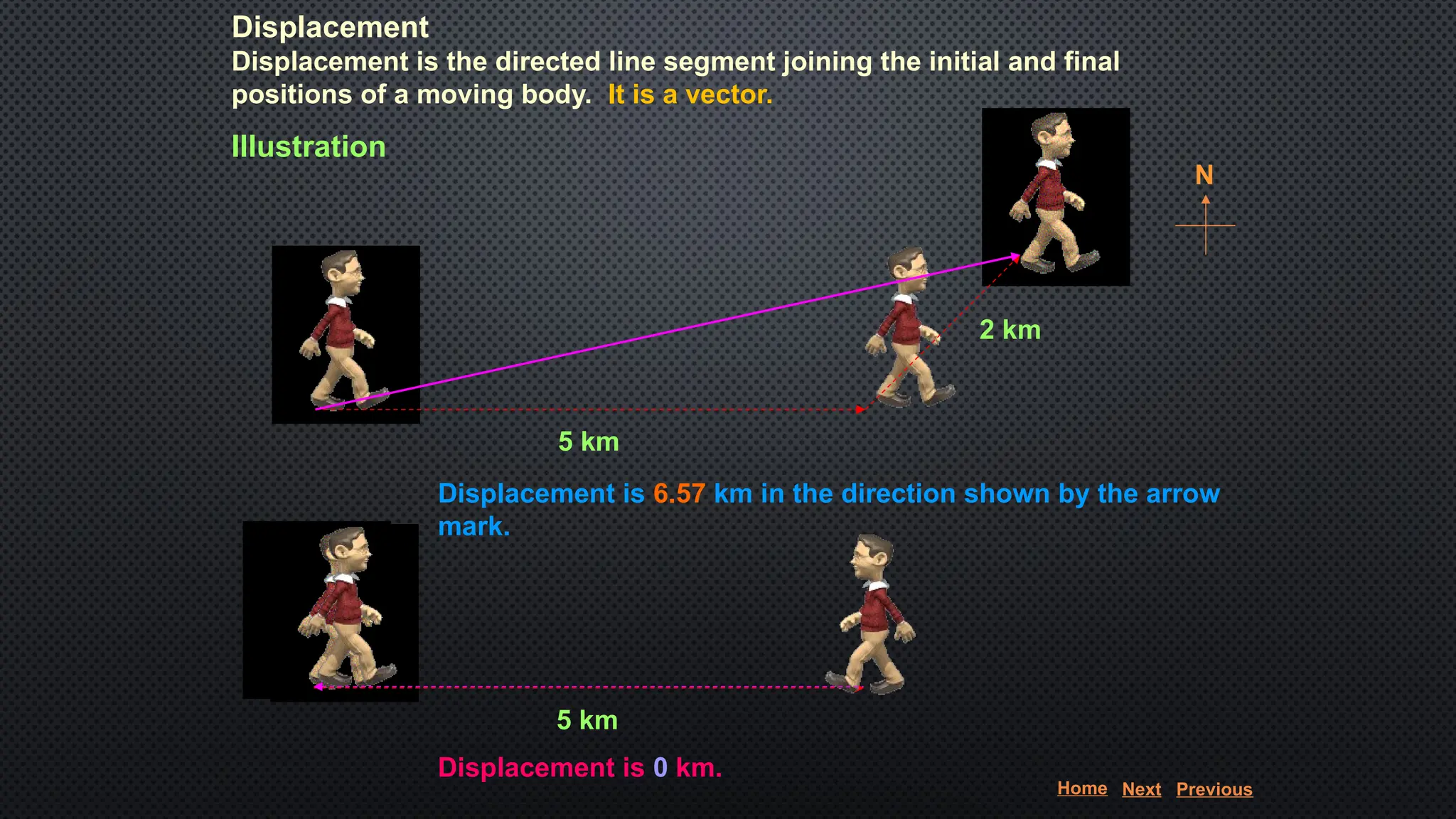
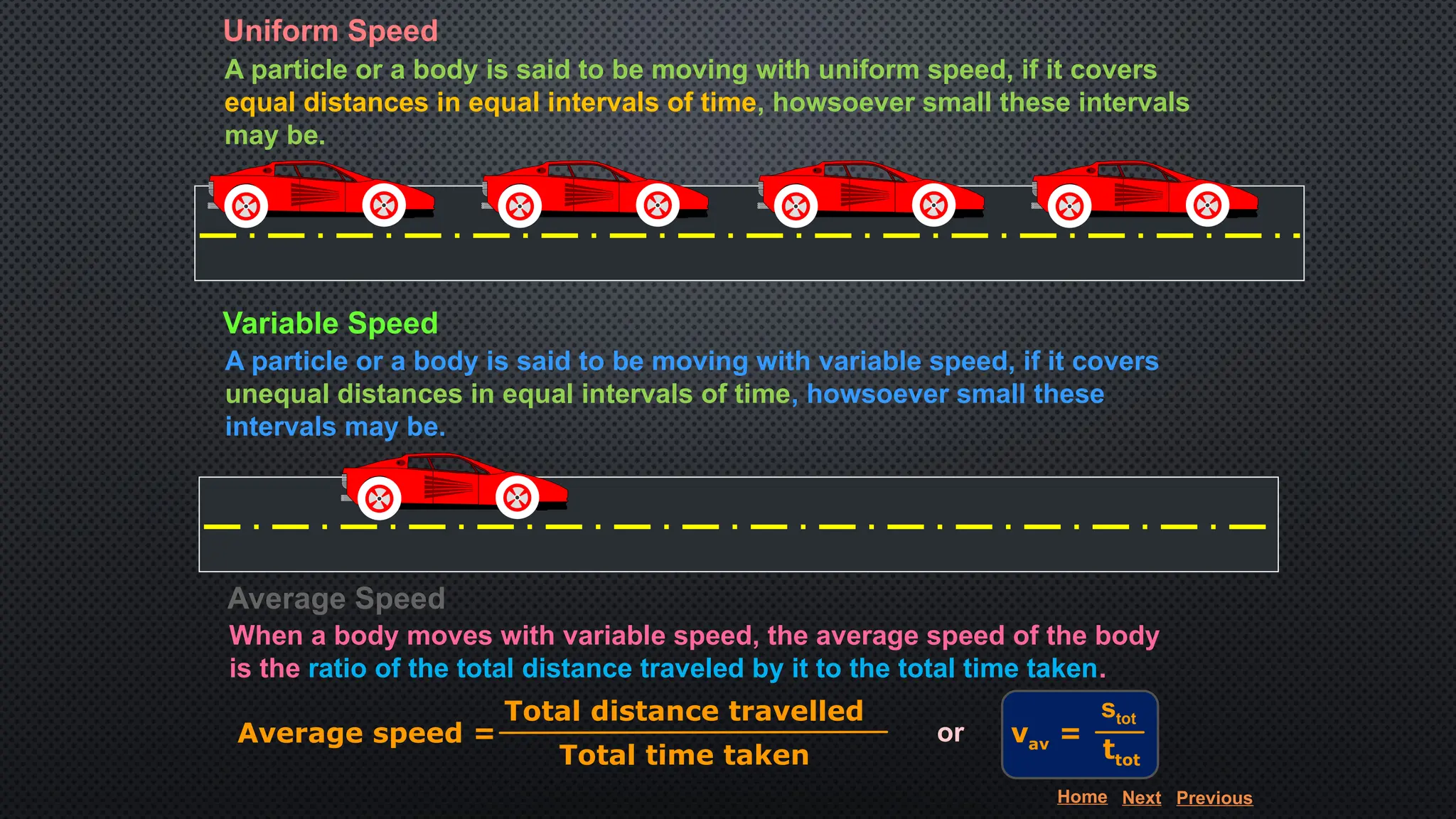
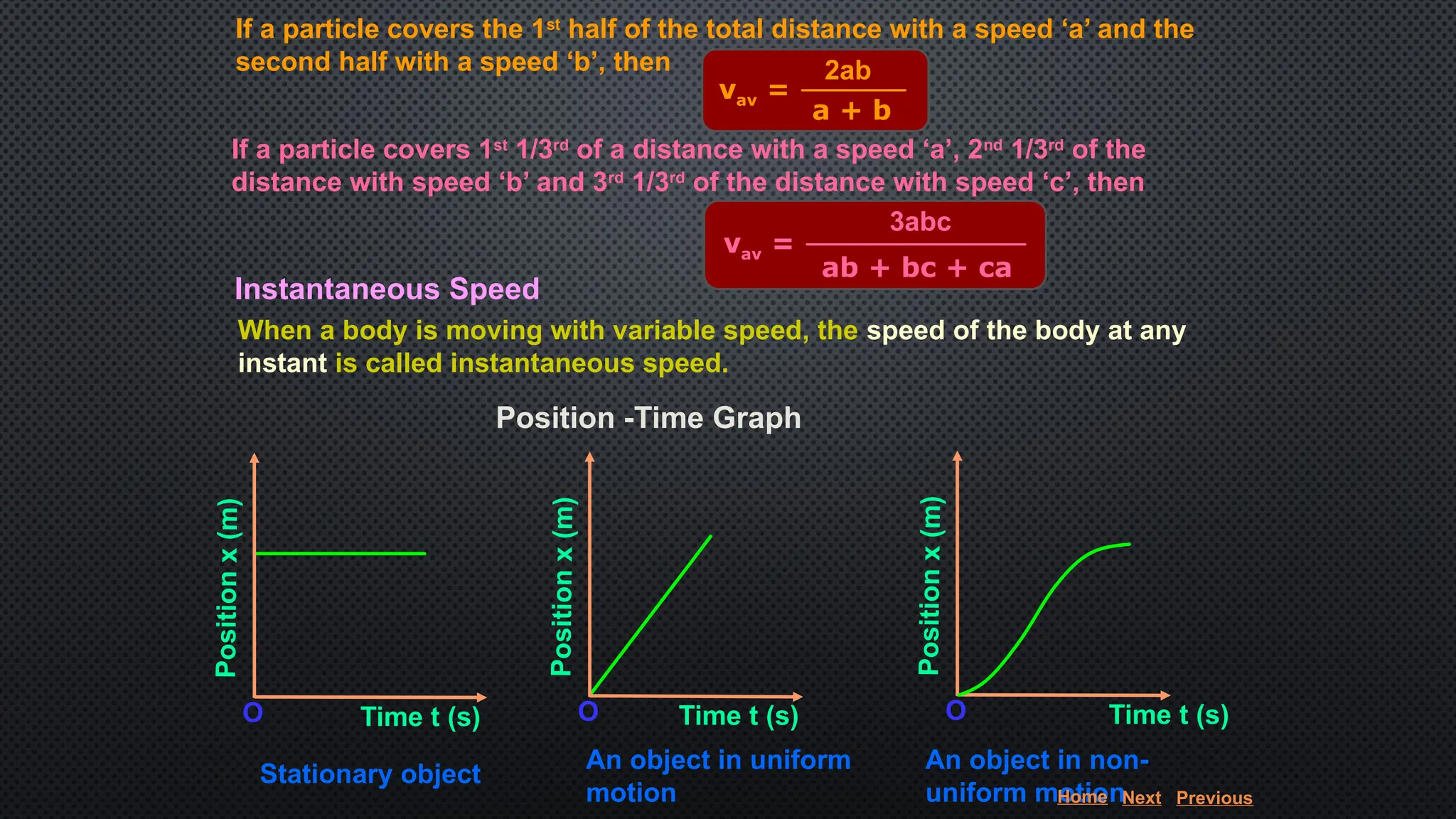
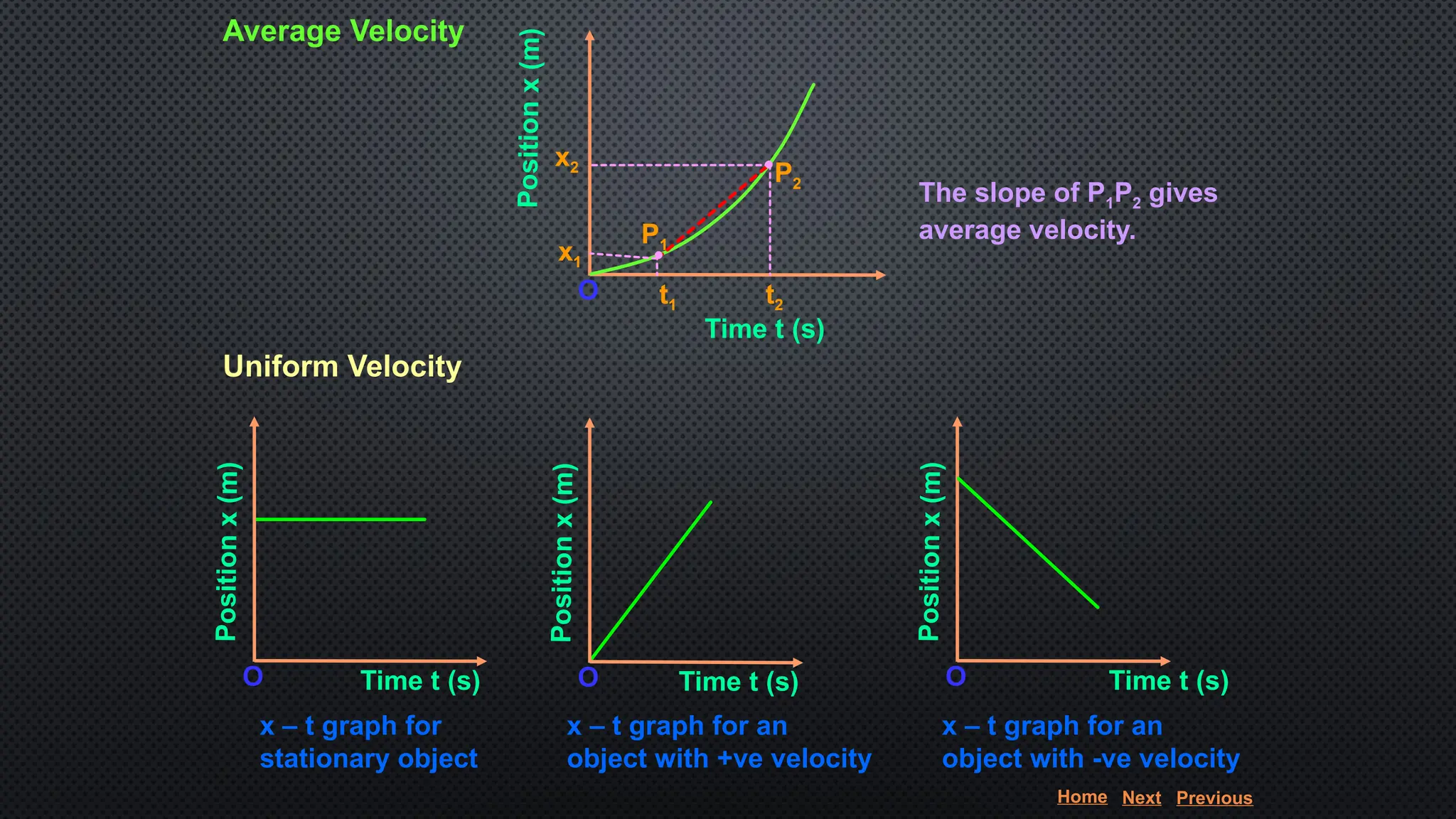
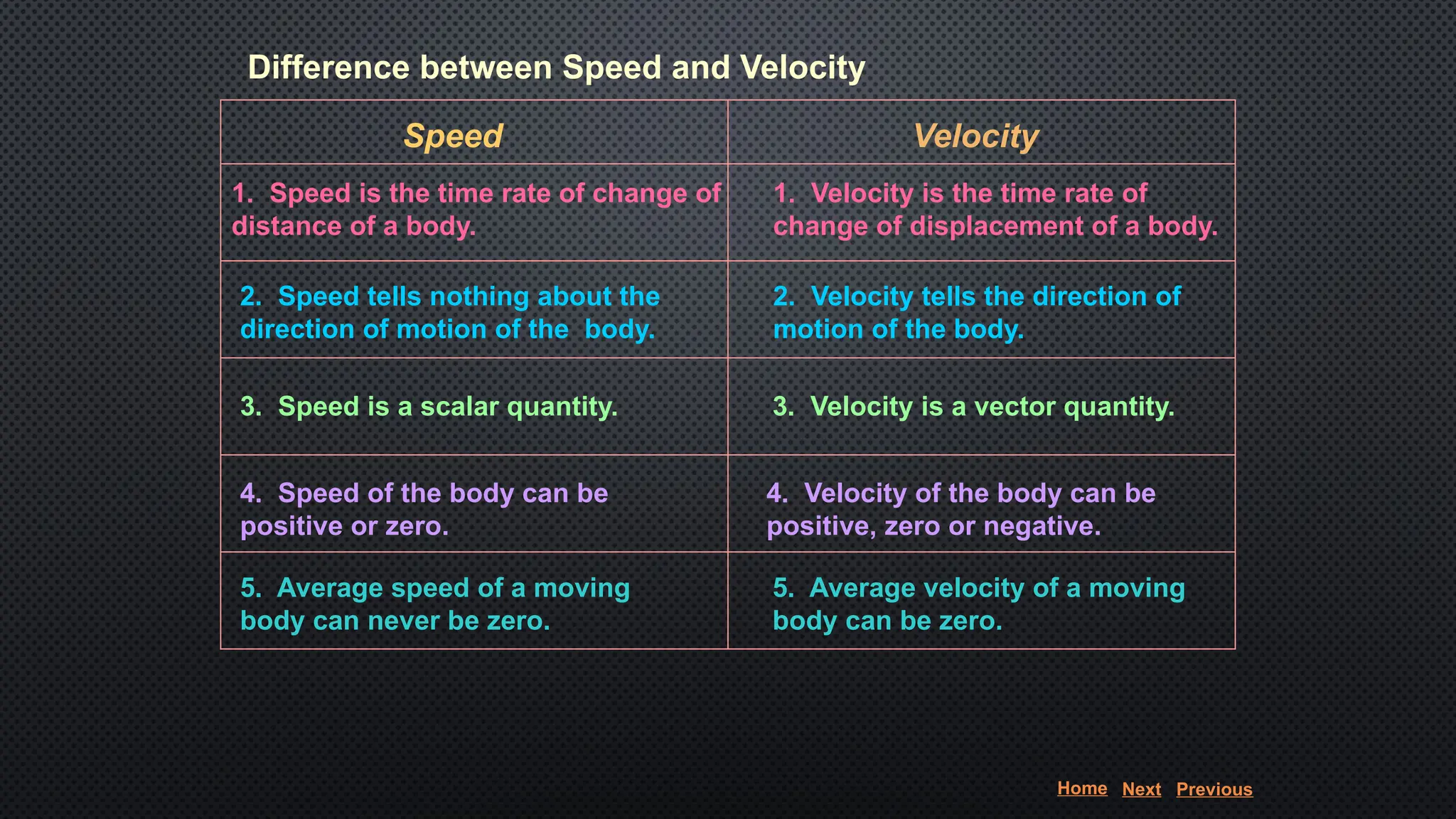
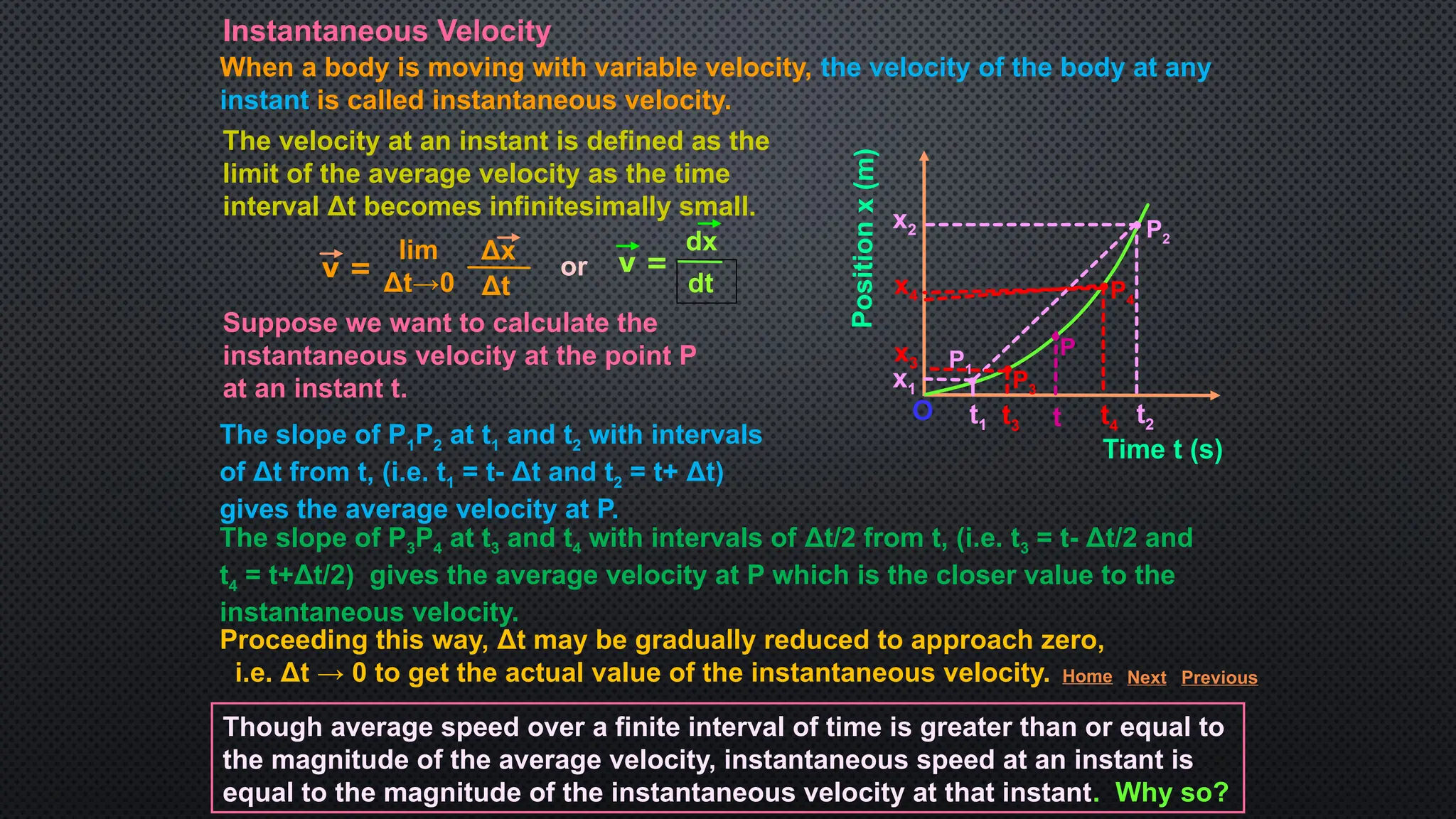
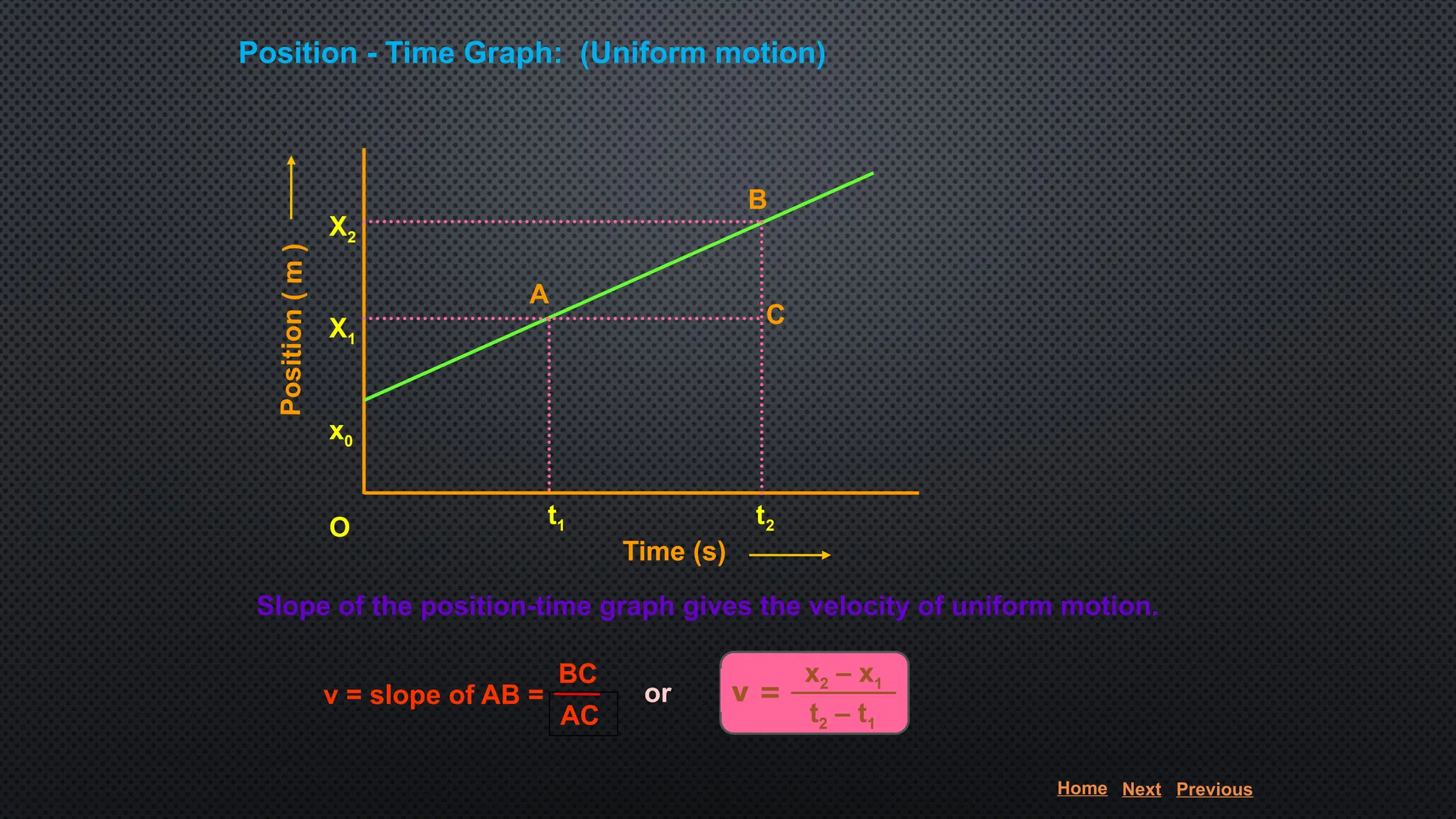
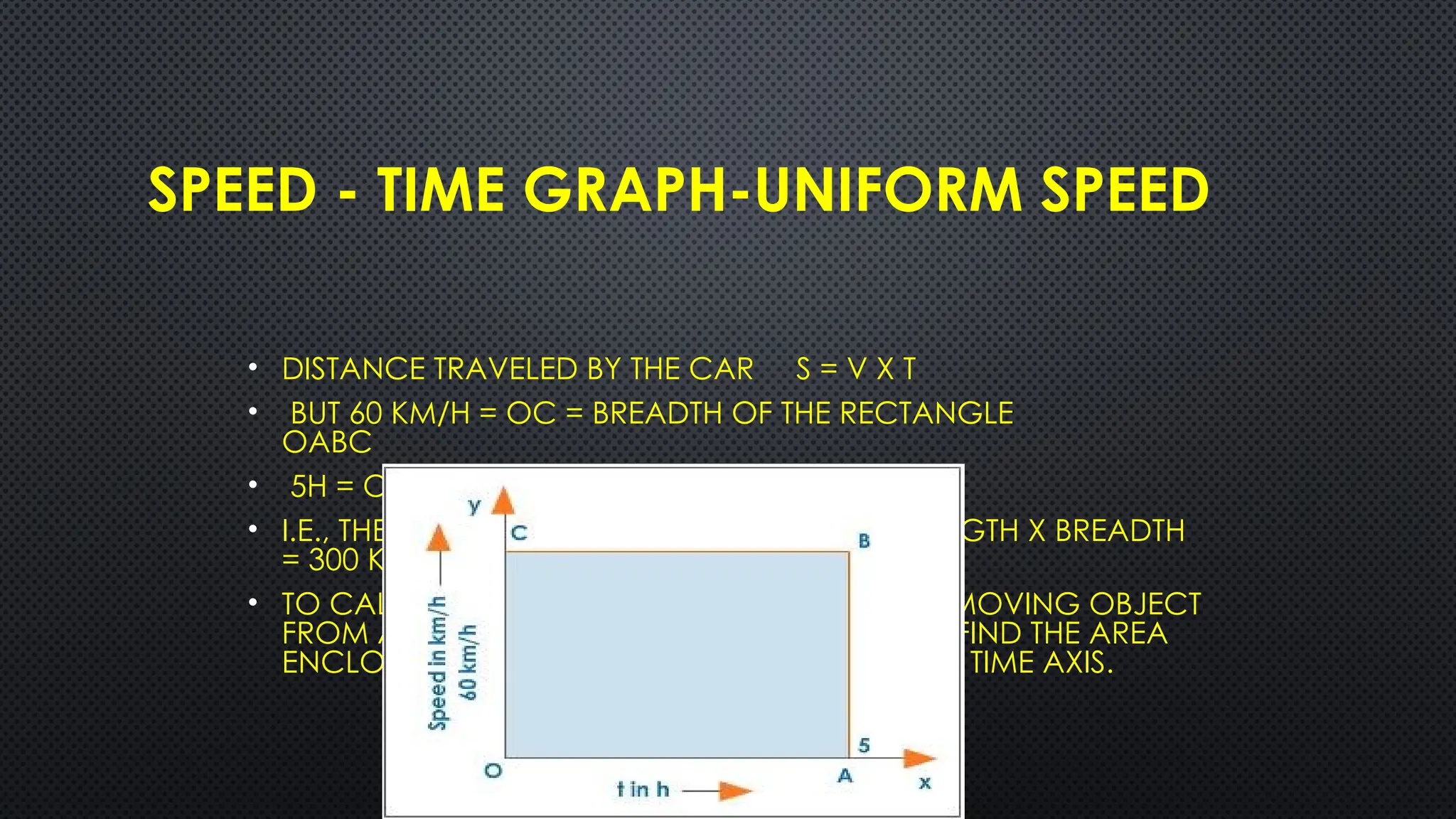
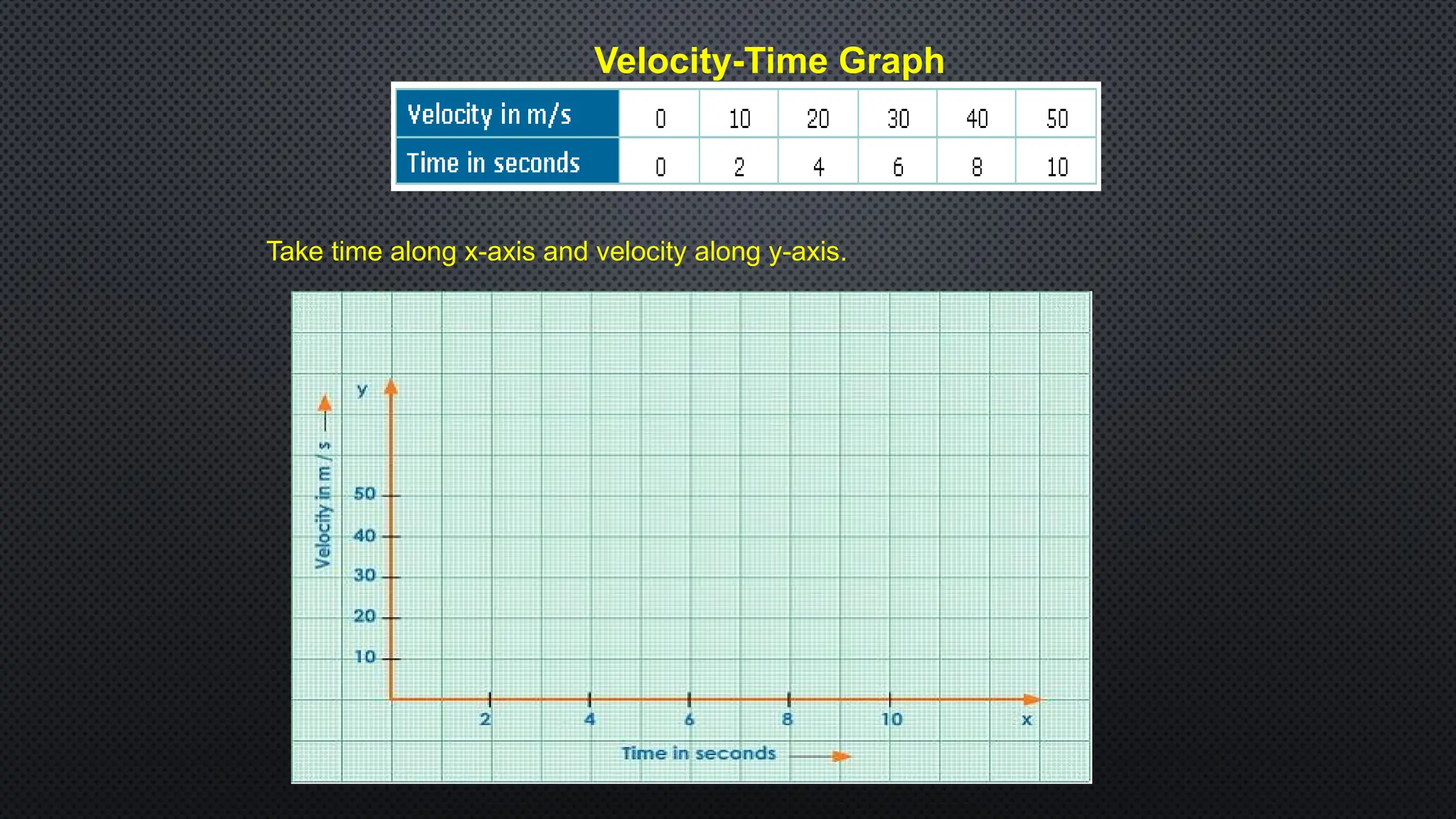
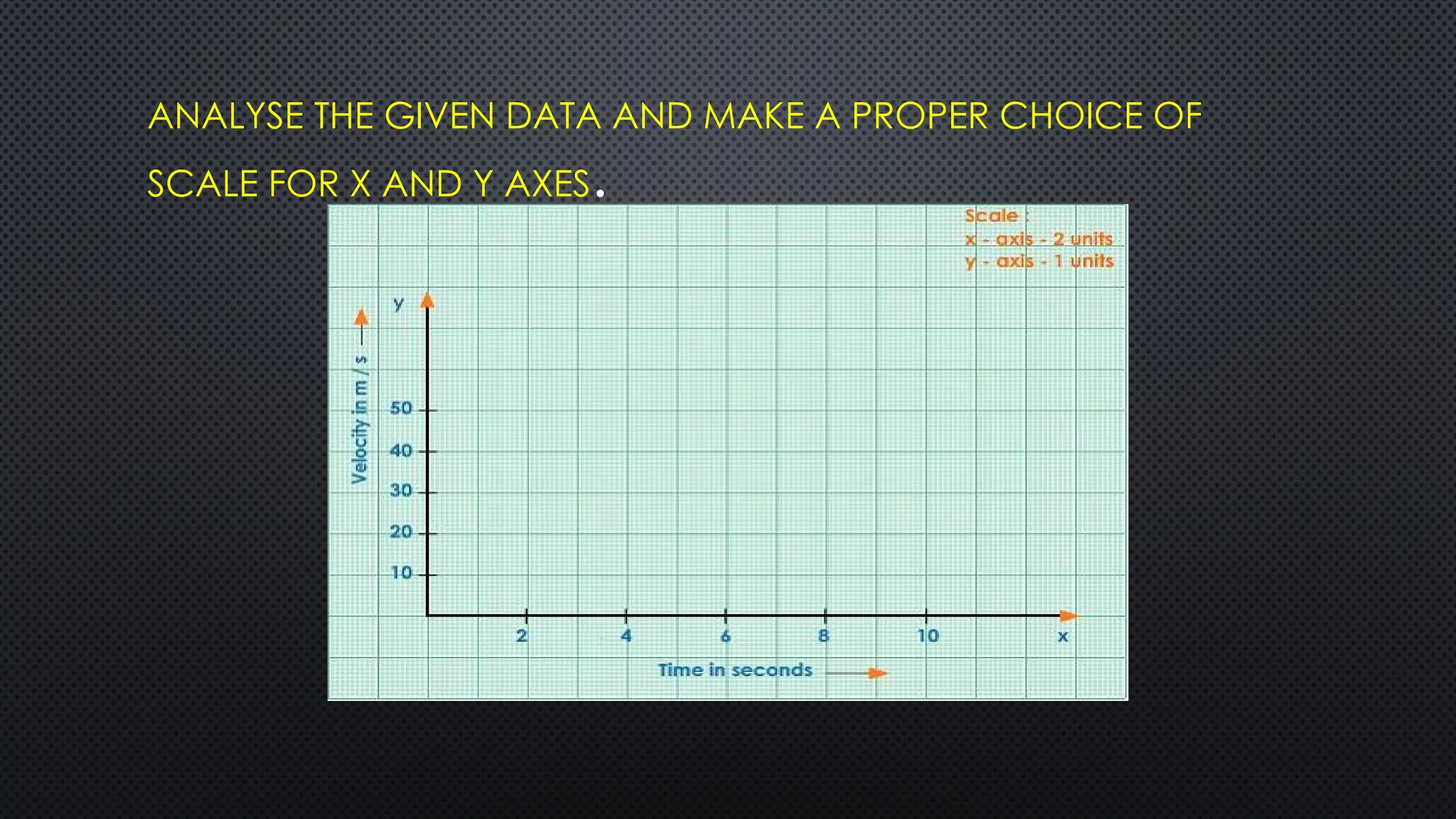
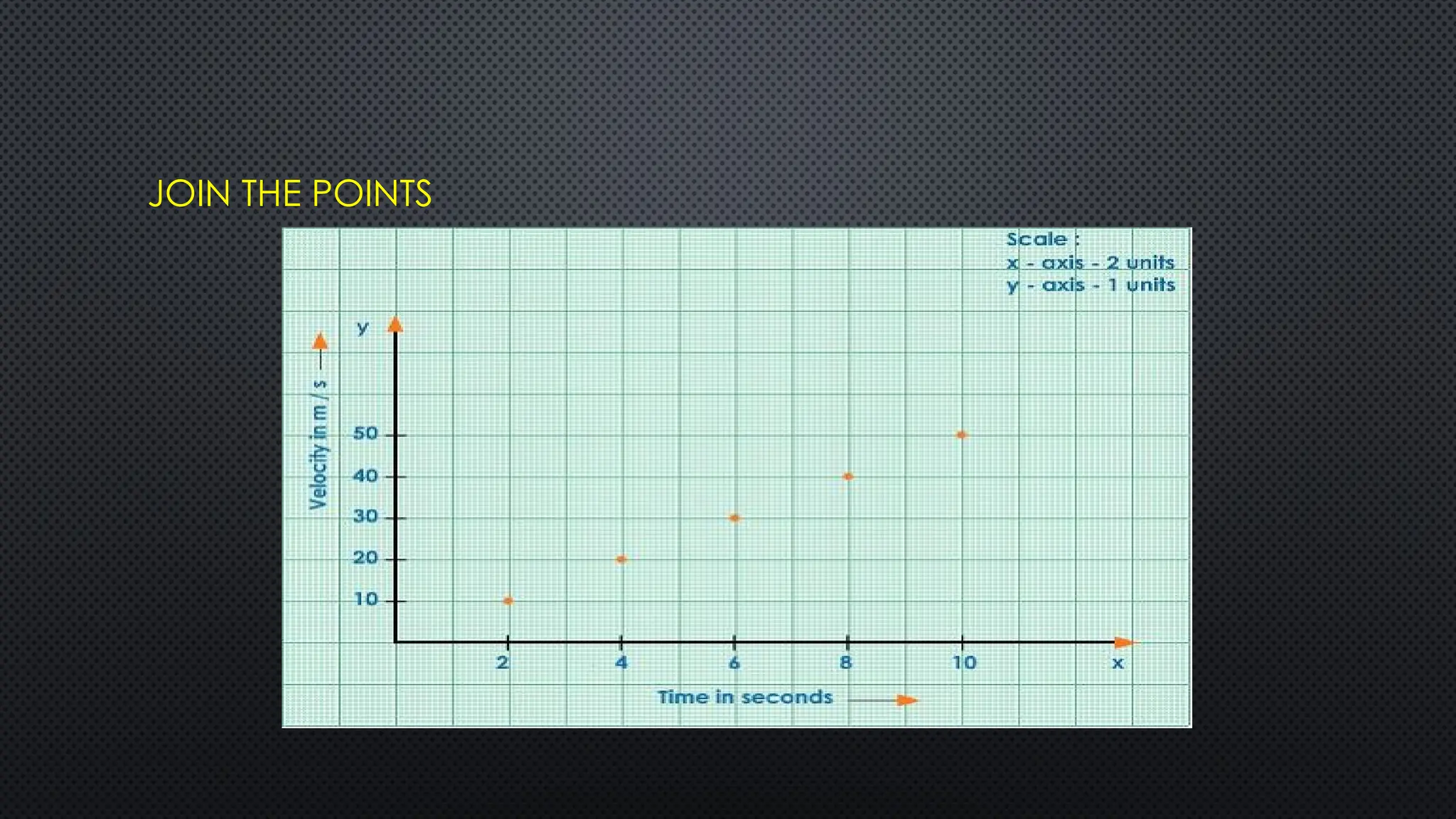
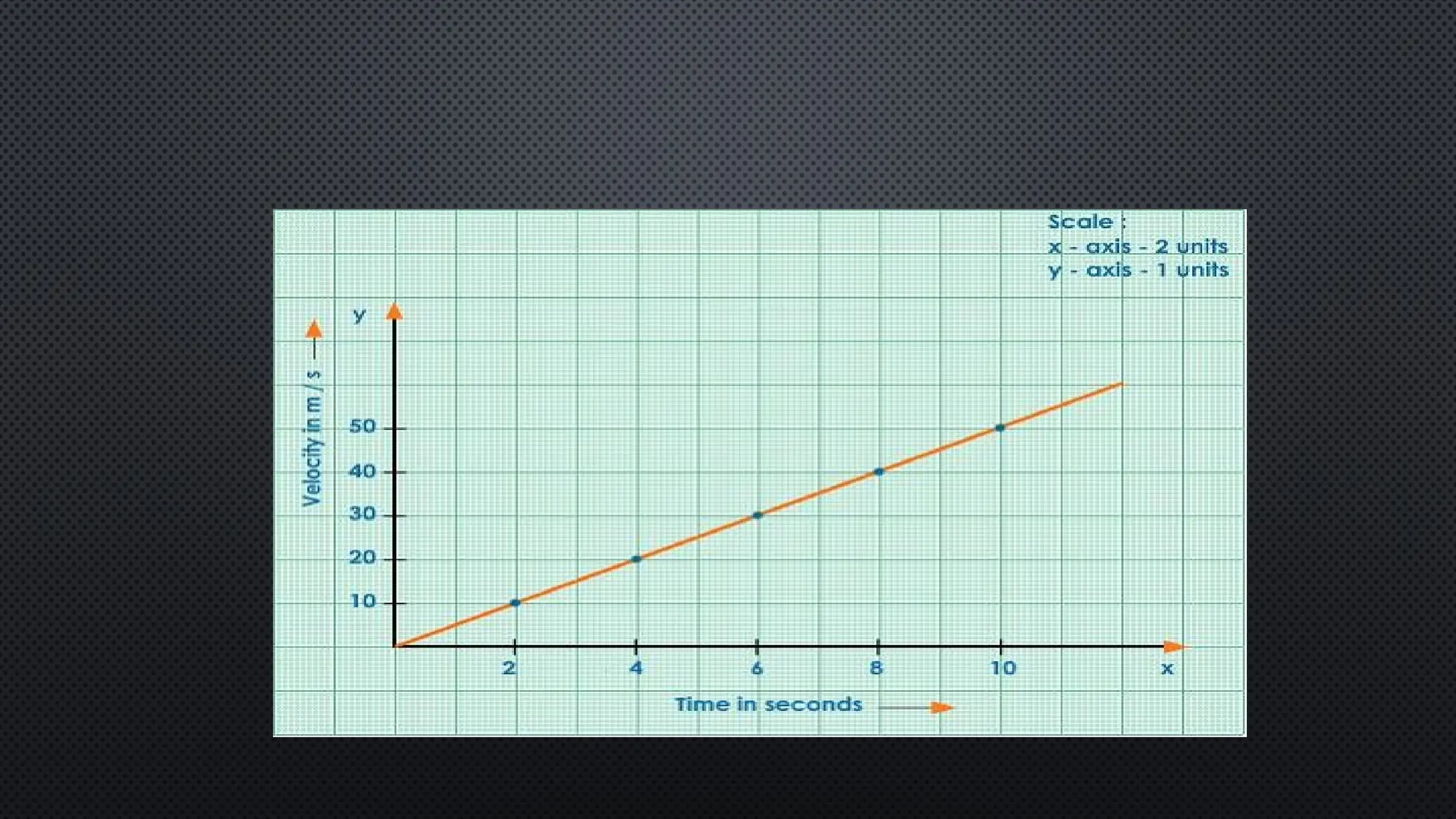
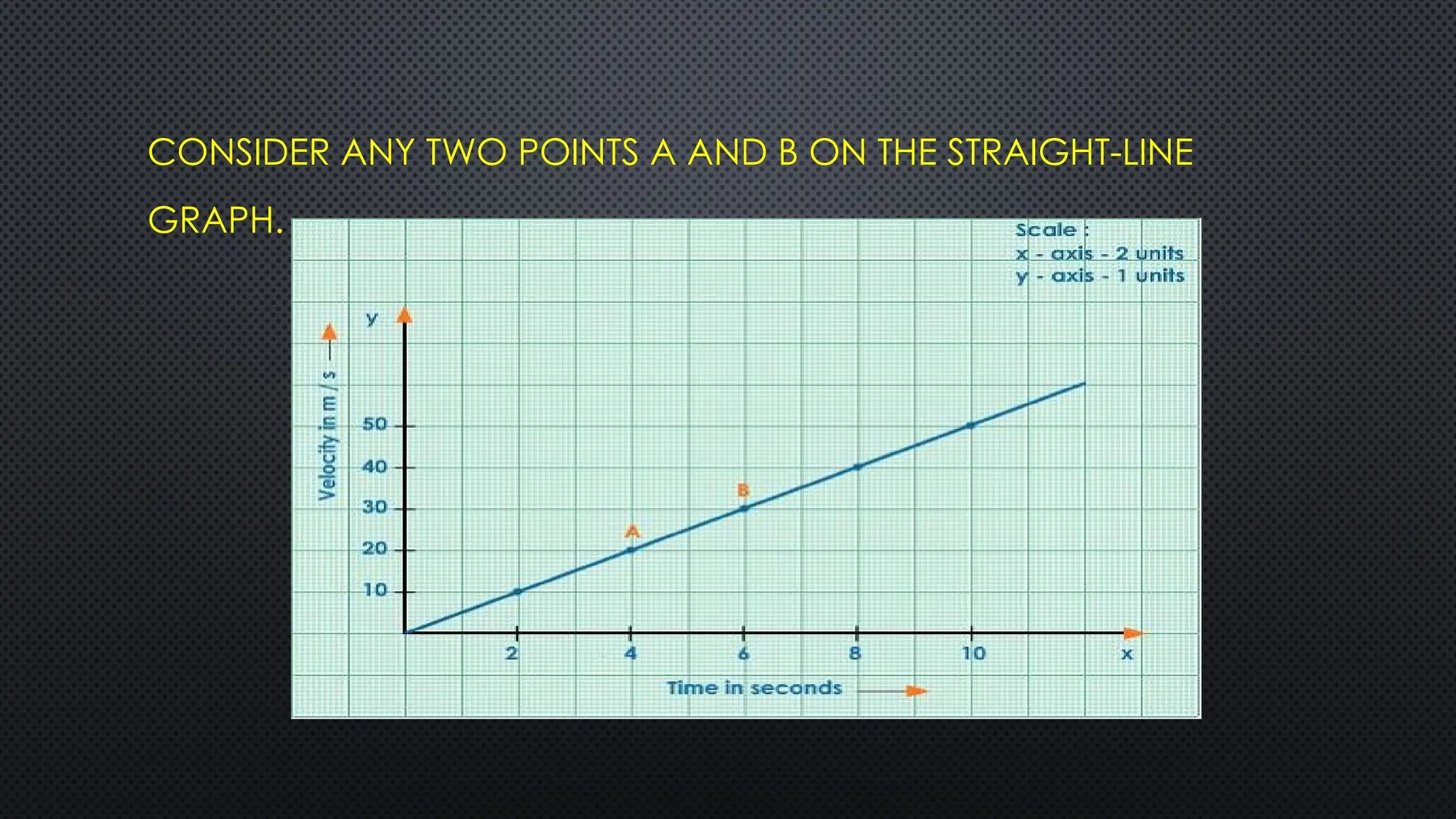
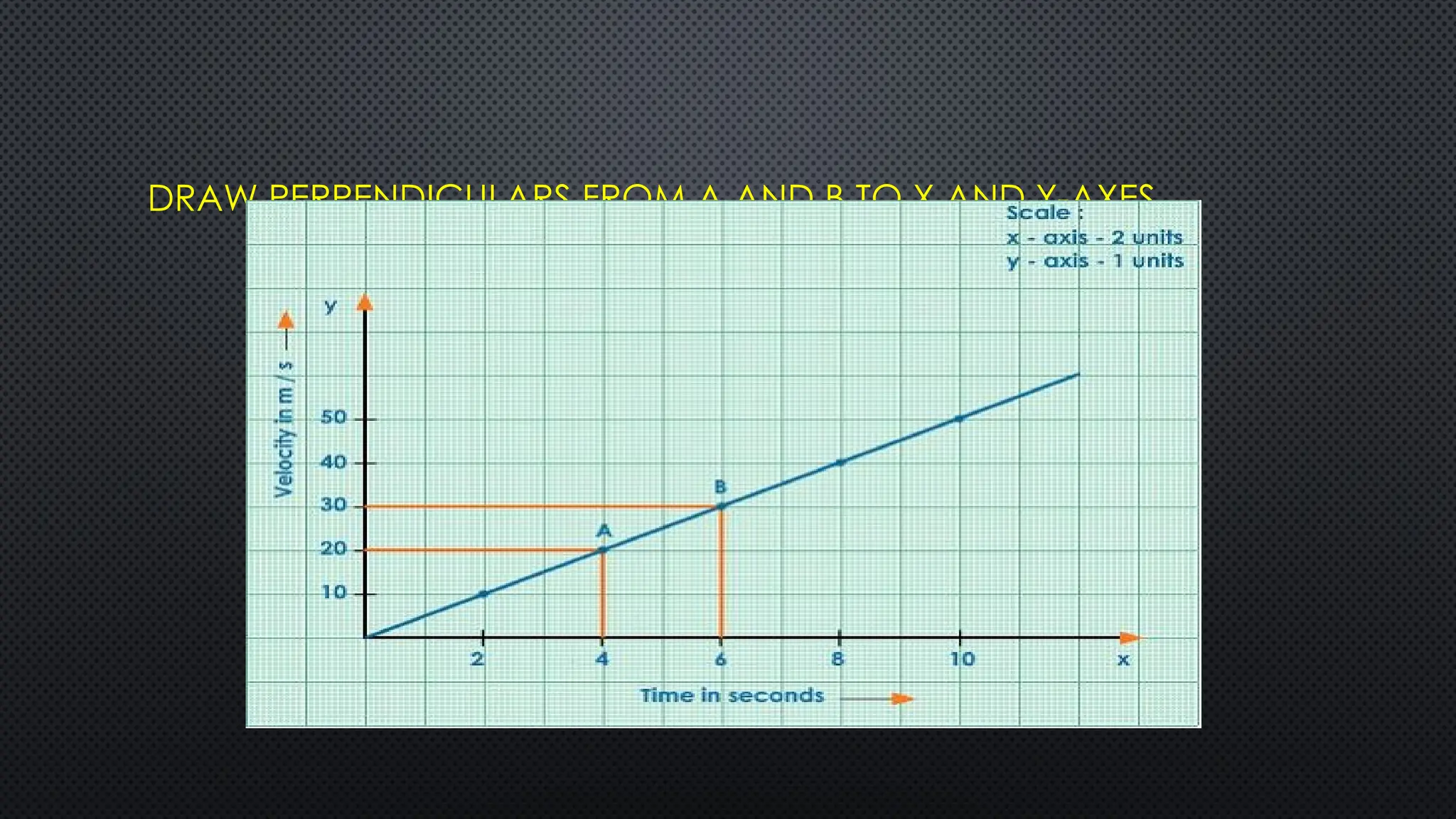
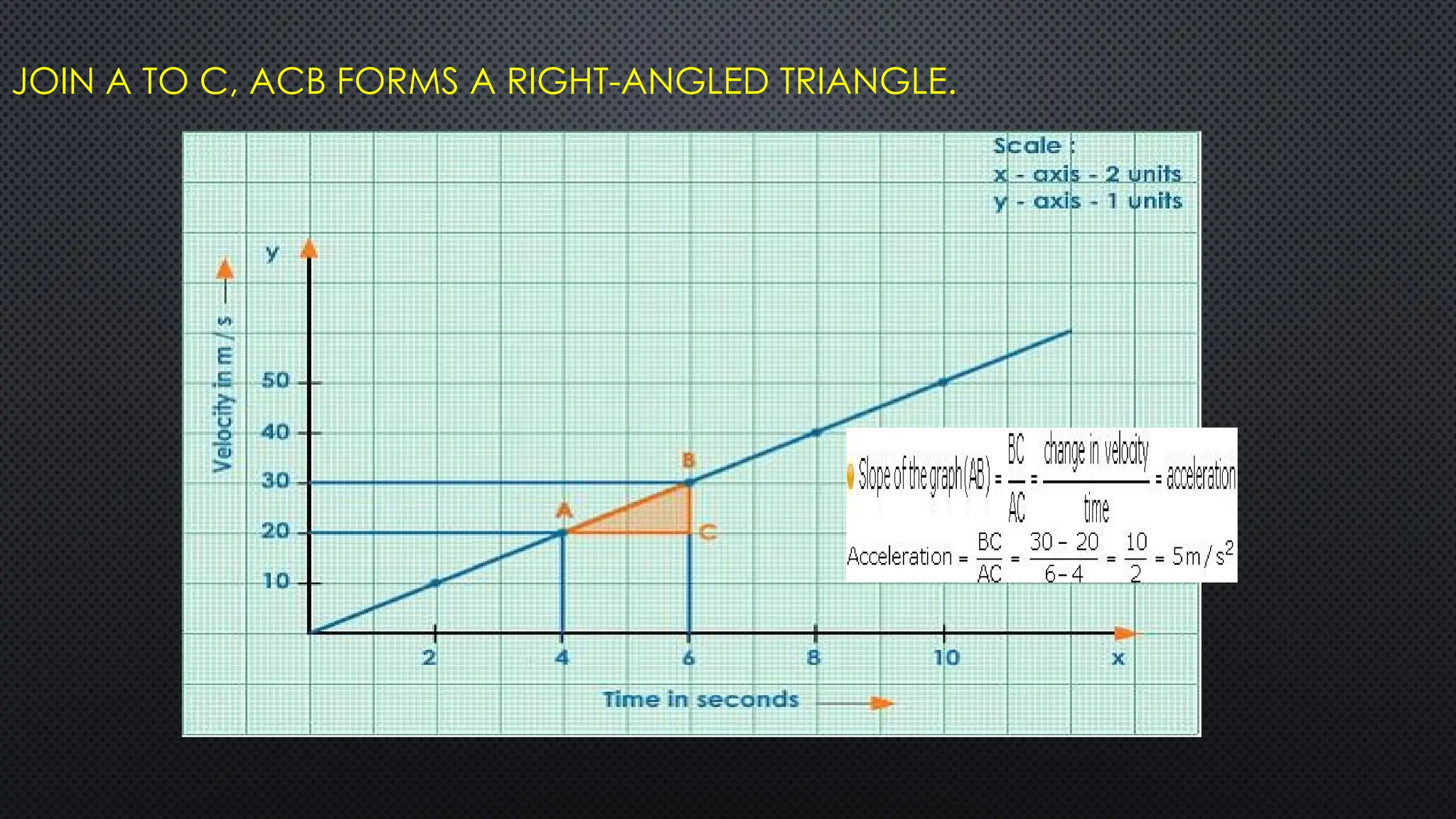
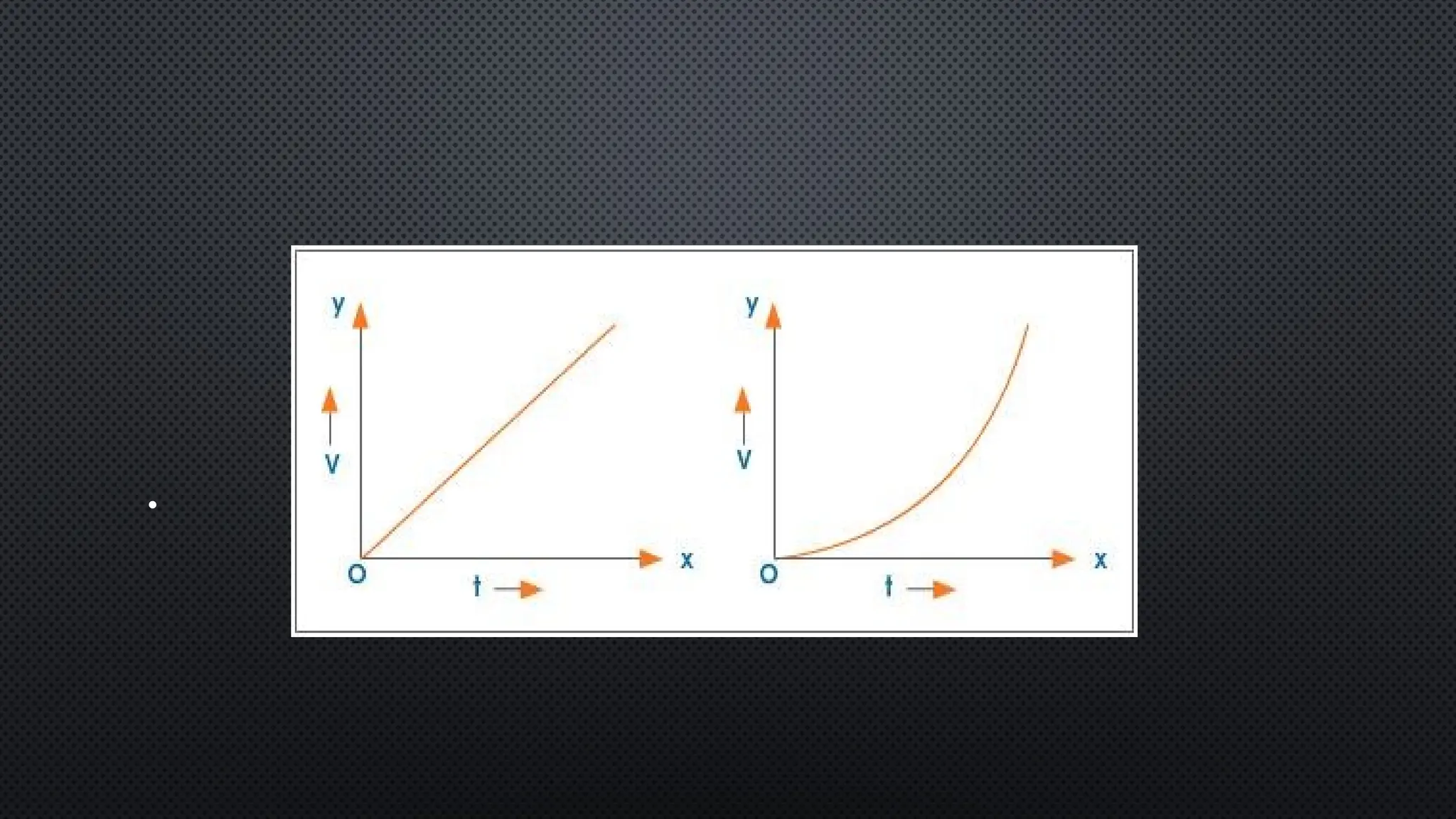
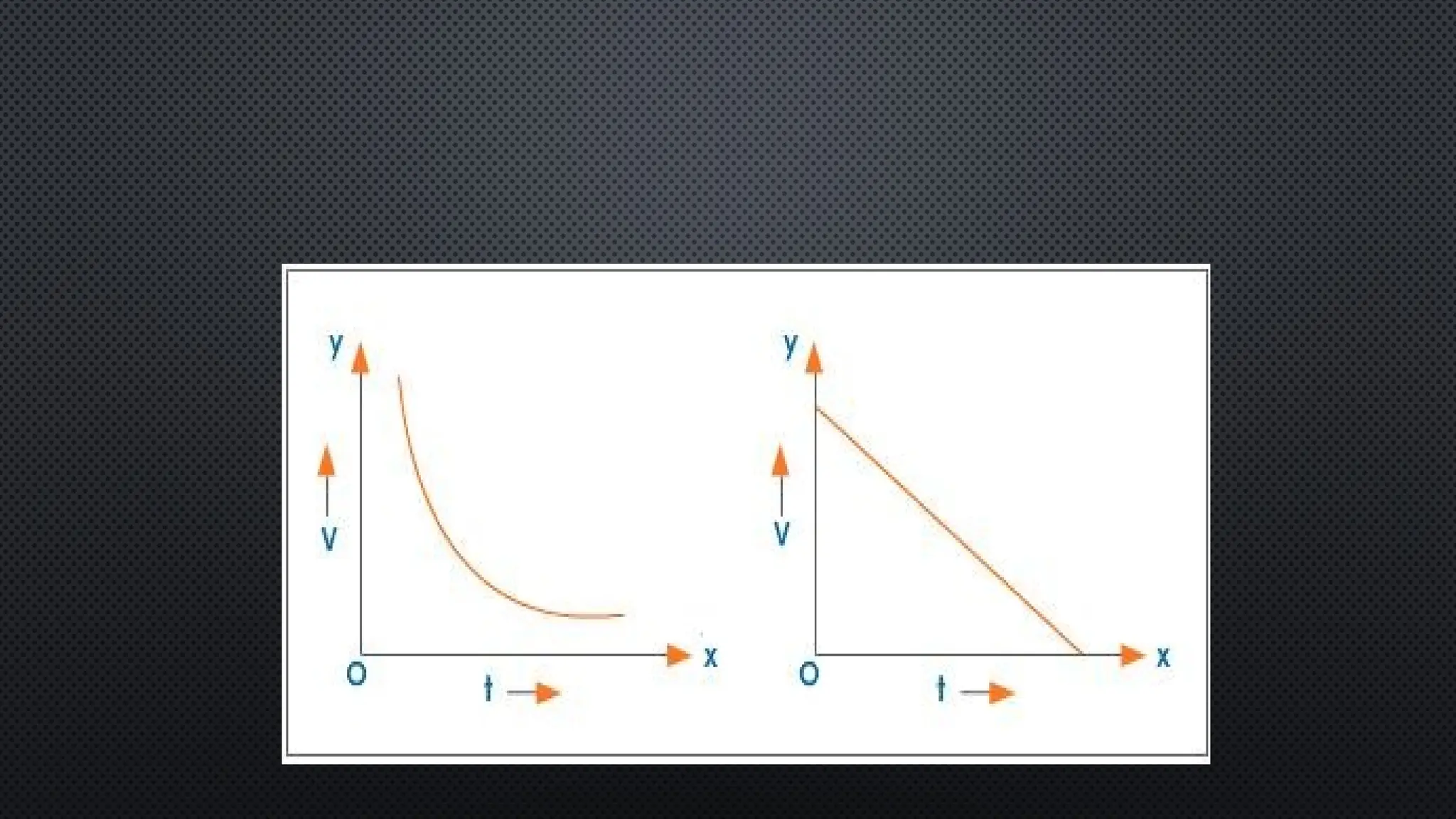
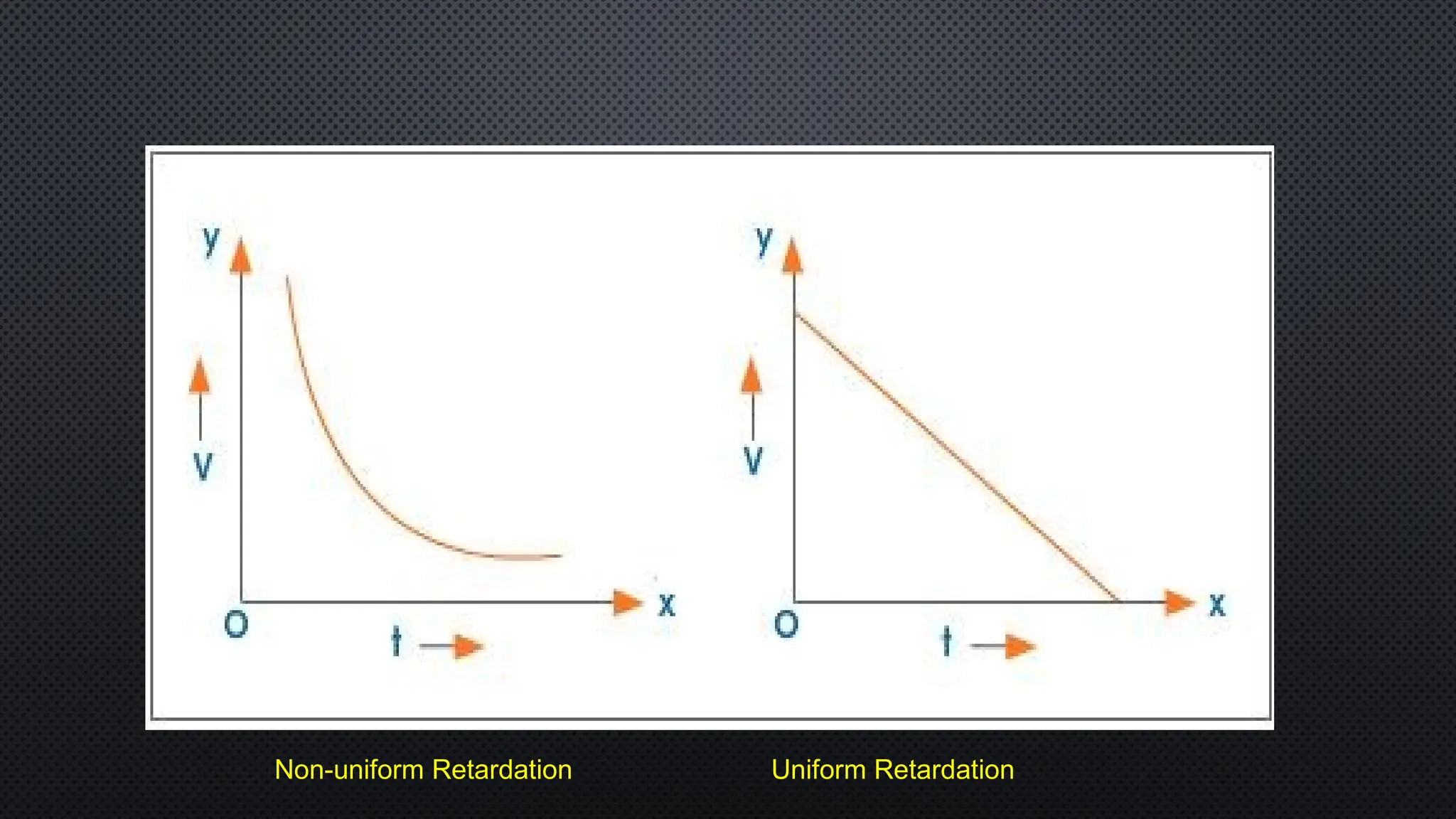
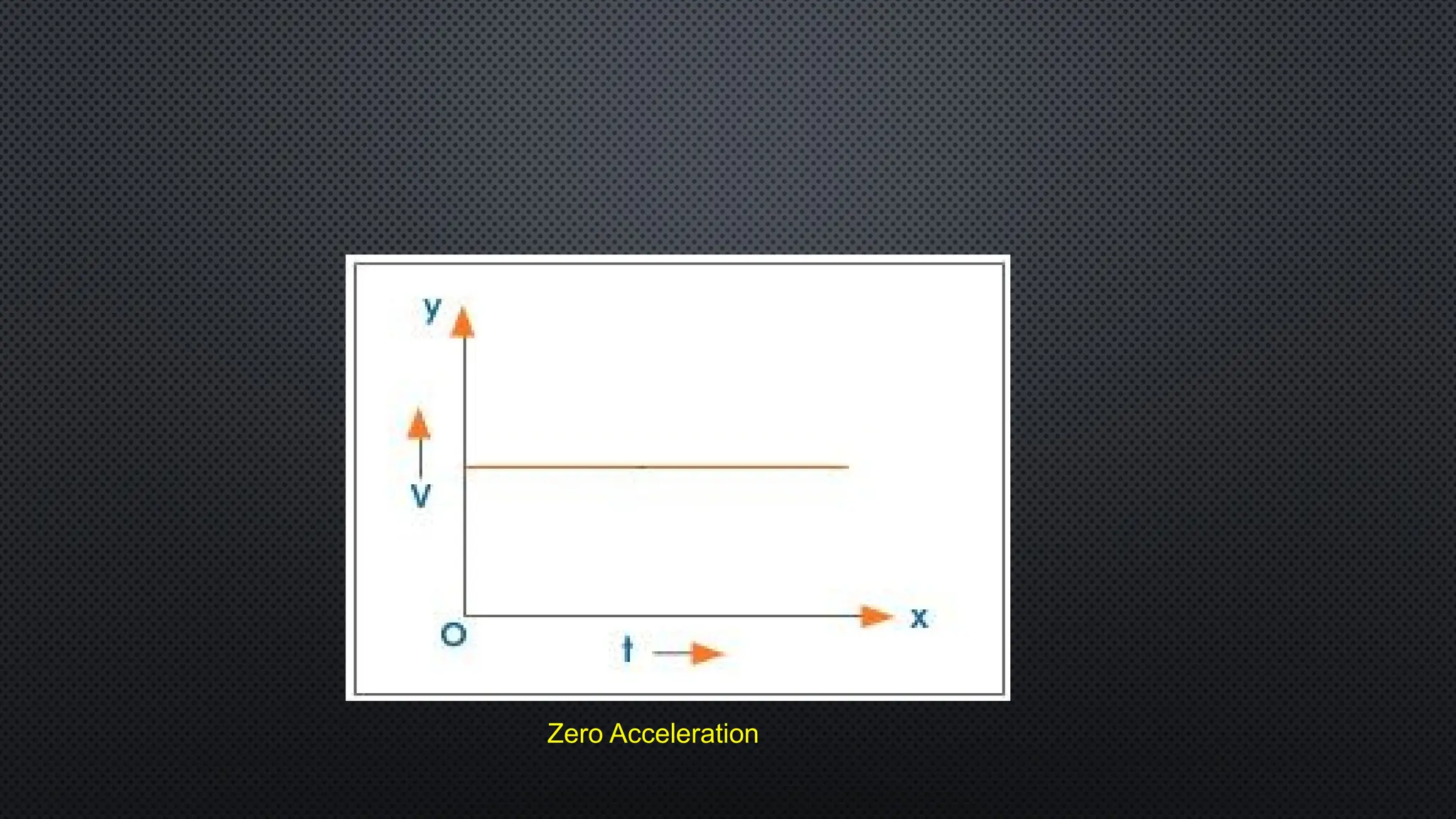
The document provides an extensive overview of motion in physics, covering concepts such as motion in one, two, and three dimensions, the distinction between speed and velocity, and essential terms like distance, displacement, and acceleration. It also introduces the branches of mechanics, including statics and dynamics, and discusses graphs and equations related to motion. Key definitions and examples illustrate the relative nature of rest and motion, along with different types of motion and their measurement.

1. MOTION IN A STRAIGHT LINE
1. Branches of Physics
2. Concept of a Point Object, Reference Point and Frame of Reference
3. Origin of Position and Time; Rest and Motion – Relative Terms
4. Motion in One, Two and Three Dimension
5. Motion in a Straight Line – Distance and Displacement, Scalar & Vector
6. Speed - Uniform, Variable, Average and Instantaneous Speed
7. Velocity - Uniform, Variable, Average(Graph) and Instantaneous(Graph)
8. Difference between Speed and Velocity
9. Uniform Motion in a Straight Line
10.Position-Time Graph and Velocity-Time Graph of Uniform Motion
11. Non-uniform Motion – Acceleration (Uniform, Non-Uniform)
12.Position-Time Graph and Velocity-Time Graph of Non-Uniform Motion
13.Equations of Motion – Normal(1st
,2nd
,3rd
) / Graphical(1st
,2nd
,3rd
) /
Calculus(1st
,2nd
,3rd
) Method of Derivation
14.Relative Velocity and Graphs
Next

2. Mechanics
Mechanics is a branch of physics that deals with the motion of a body due to
the application of force.
The two main branches of mechanics are:
(a) Statics and
(b) Dynamics
Statics
Statics is the study of the motion of an object under the effect of forces in
equilibrium.
Dynamics
Dynamics is the study of the motion of the objects by taking into account the
cause of their change of states (state of rest or motion).
Dynamics is classified into (i) Kinematics and (ii) Kinetics
Kinematics
The study of the motion of the objects without taking into account the cause
of their motion is called kinematics.
Kinetics
Kinetics is the study of motion which relates to the action of forces causing
the motion and the mass that is moved.
Home Next Previous

3. Concept of a Point Object
In mechanics, a particle is a geometrical mass point or a material body of
negligible dimensions. It is only a mathematical idealization.
Examples:
In practice, the nearest approach to a particle is a body, whose size is much
smaller than the distance or the length involved. Home Next Previous

4. POSITION, PATH LENGTH AND DISPLACEMENT
Reference Point
Consider a rectangular coordinate system consisting of three mutually
perpendicular axes, labeled X-, Y-, and Z- axes. The point of intersection of
these three axes is called origin (O) and serves as the reference point. The
coordinates (x, y, z) of an object describe the position of the object with
respect to this coordinate system.
Frame of reference
The coordinate system along with a clock to measure
the time constitutes a frame of reference.
Positive direction
The positive direction of an axis is in the direction
of increasing numbers (coordinates).
Negative direction
The negative direction of an axis is in the direction
of decreasing numbers (coordinates).
X
Z
Y
O
Home Next Previous

5. While describing motion, we use reference point or origin
w.r.t. which the motion of other bodies are observed.
We can use any object as reference point. For example, a
car at rest or in motion can be used as reference point.
When you travel in a bus or train you can see the trees,
buildings and the poles moving back.
To a tree, you are moving forward and to you, the trees are
moving back.
Both, you and the trees, can serve as reference point but
motion can not be described without reference point.
What effect do you get when you play video game involving
car racing?
Home Next Previous

6. 1. The distance measured to the right of the origin of the position axis is
taken positive and the distance measured to the left of the origin is taken
negative.
2. The origin for position can be shifted to any point on the position axis.
3. The distance between two points on position-axis is not affected due to
the shift in the origin of position-axis.
Origin, unit and direction of position measurement of an object
-60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60
70
(m)
+X
-X
Origin, unit and sense of passage of time
1. The time measured to the right of the origin of the time-axis is taken
positive and the time measured to the left of the origin is taken negative.
2. The origin of the time-axis can be shifted to any point on the time-axis.
3. The negative time co-ordinate of a point on time-axis means that object
reached that point a time that much before the origin of the time-axis i.e. t = 0.
4. The time interval between two points on time-axis is not affected due to the
shift in the origin of time-axis.
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7(s)
+t
-t
Home Next Previous

7. When the same point is chosen as origins for position and time:
O A B C
x = 0 x = 30 km x = 40 km x = 55 km
t = 0 t = 6 h t = 8 h t = 11 h
When the different points are chosen as origins for position
and time:
O A B C
x = - 40 km x = -10 km x = 0 km x = 15 km
t = -6 h t = 0 t = 2 h t = 5 h
Origin for position and time
Origin for time Origin for position
Home Next Previous

8. Rest and Motion
A ball is at rest w.r.t. a stationary man.
A car is at rest w.r.t. a stationary man.
A ball is moving w.r.t. a stationary man.
A car is moving w.r.t. a stationary man.
Home Next Previous

9. Rest
A body is said to be at rest if its position remains constant with respect to its
surroundings or frame of reference.
Examples: Mountains, Buildings, etc.
Motion
A body is said to be in motion if its position is changing with respect to its
surroundings or frame of reference.
Examples: 1. Moving cars, buses, trains, cricket ball, etc.
2. All the planets revolving around the Sun
3. Molecules of a gas in motion above 0 K
Rest and Motion are relative terms:
An object which is at rest can also be in motion simultaneously.
Eg. The passengers sitting in a moving train are at rest w.r.t. each other but
they are also in motion at the same time w.r.t. the objects like trees,
buildings, etc.
Home Next Previous

10. Rest and Motion are Relative Terms
Car is moving w.r.t. stationary man.
Car is moving w.r.t. stationary man.
Home Next Previous

11. Rest and Motion are Relative Terms
Both the cars are at rest w.r.t. stationary man.
Both the cars are moving w.r.t. a stationary man.
Both the cars are at rest w.r.t. each other.
Home Next Previous

12. In the examples of motion of ball and car, man is considered to be
at rest (stationary).
But, the man is standing on the Earth and the Earth itself moves
around the Sun as well as rotates about its own axis.
Therefore, man is at rest w.r.t. the Earth but is rotating and
revolving around the Sun.
That is why rest and motion are relative terms !
Rest and Motion are Relative Terms – How?
Home Next Previous

13. A ship is sailing in the ocean. Man-A in the ship is running on the board in
the direction opposite to the direction of motion of the ship. Man-B in
the ship is standing and watching the Man-A.
Analyse the following cases to understand motion and rest !
1. Man-A w.r.t. Man-B
2. Man-A w.r.t. ship
3. Man-B w.r.t. ship
4. Ship w.r.t. still water
5. Man-A w.r.t. still water
6. Man-B w.r.t. still water
7. Ocean w.r.t. the Earth
8. Ocean w.r.t. the Sun
9. Earth w.r.t. the Sun
10.Ship w.r.t. the Sun
11. The Sun w.r.t. Milky Way Galaxy
12. Milky Way Galaxy w.r.t. other galaxies
Your imagination should not ever stop !
Home Next Previous

14. MOTION IN ONE, TWO OR THREE DIMENSIONS
One Dimensional Motion
The motion of the object is said to be one dimensional if only one of the three
coordinates is required to be specified with respect to time. It is also known
as rectilinear motion.
In such a motion the object moves in a straight line.
Example: A train moving in straight track, a man walking in a narrow, leveled
road, etc.
Two Dimensional Motion
The motion of the object is said to be two dimensional if two of the three
coordinates are required to be specified with respect to time.
In such a motion the object moves in a plane.
Example: Ant moving on a floor, a billiard ball moving on a billiard table, etc.
Three Dimensional Motion
The motion of the object is said to be three dimensional if all the three
coordinates are required to be specified with respect to time.
Such a motion takes place in space.
Example: A flying airplane, bird, kite, etc.
Home Next Previous

15. N
5 km
2 km
5 km
Distance travelled is 7 km.
Distance travelled is 10 km.
Path
The line joining the successive positions of a moving body is called its path.
The length of the actual path between the initial and final position gives the
distance travelled by the body. Distance is a scalar.
Motion in a Straight Line
Illustration
Home Next Previous

16. N
5 km
2 km
5 km
Displacement is 6.57 km in the direction shown by the arrow
mark.
Displacement is 0 km.
Displacement
Displacement is the directed line segment joining the initial and final
positions of a moving body. It is a vector.
Illustration
Home Next Previous

17. If a body changes from one position x1 to another position x2, then the
displacement Δx in time interval Δt = t2 – t1, is Δx = x2 – x1
Conclusions about displacement
1. The displacement is a vector quantity.
2. The displacement has units of length.
3. The displacement of an object in a given time interval can be
positive, zero or negative.
4. The actual distance travelled by an object in a given time interval
can be equal to or greater than the magnitude of the
displacement.
5. The displacement of an object between two points does not tell
exactly how the object actually moved between those points.
6. The displacement of a particle between two points is a unique
path, which can take the particle from its initial to final position.
7. The displacement of an object is not affected due to the shift in
the origin of the position-axis.
Home Next Previous

18. Scalar
Scalar quantity is a physical quantity which has magnitude only.
Eg.: Length, Mass, Time, Speed, Energy, etc.
Vector
Vector quantity is a physical quantity which has both magnitude as well as
direction.
Eg.: Displacement, Velocity, Acceleration, Momentum, Force, etc.
S. No. Distance Displacement
1
2
Distance is a scalar quantity. Displacement is a vector quantity.
Distance travelled by a
moving body cannot be zero.
Final displacement of a moving
body can be zero.
A C
B
Distance
Displacement
Home Next Previous

19. Speed
The time rate of change of distance of a particle is called speed.
Speed =
Distance travelled
Time taken
or v =
s
t
Note:
1. Speed is a scalar quantity.
2. Speed is either positive or zero but never negative.
3. Speed of a running car is measured by ‘speedometer’.
4. Speed is measured in
i) cm/s (cm s-1
) in cgs system of units
ii) m/s (m s-1
) in SI system of units and
iii) km/h (km.p.h., km h-1
) in practical life when distance and time
involved are large.
Home Next Previous

20. Uniform Speed
A particle or a body is said to be moving with uniform speed, if it covers
equal distances in equal intervals of time, howsoever small these intervals
may be.
Variable Speed
A particle or a body is said to be moving with variable speed, if it covers
unequal distances in equal intervals of time, howsoever small these
intervals may be.
Average Speed
When a body moves with variable speed, the average speed of the body
is the ratio of the total distance traveled by it to the total time taken.
Average speed =
Total distance travelled
Total time taken
or vav =
stot
ttot
Home Next Previous

21. Instantaneous Speed
When a body is moving with variable speed, the speed of the body at any
instant is called instantaneous speed.
If a particle covers the 1st
half of the total distance with a speed ‘a’ and the
second half with a speed ‘b’, then
If a particle covers 1st
1/3rd
of a distance with a speed ‘a’, 2nd
1/3rd
of the
distance with speed ‘b’ and 3rd
1/3rd
of the distance with speed ‘c’, then
vav =
2ab
a + b
vav =
3abc
ab + bc + ca
Position -Time Graph
Posit
ion
x
(m)
Time t (s)
O
Posit
ion
x
(m)
Time t (s)
O
Posit
ion
x
(m)
Time t (s)
O
Stationary object
An object in uniform
motion
An object in non-
uniform motion
Home Next Previous

22. Velocity
The time rate of change of displacement of a particle is called velocity.
Velocity =
Displacement
Time taken
or v =
s
t
1 m/s = km/h
18
5
1 km/h = m/s
5
18
Note:
1. Velocity is a vector quantity.
2. Direction of velocity is the same as the direction of displacement of the
body.
3. Velocity can be either positive, zero or negative.
4. Velocity can be changed in two ways:
i) by changing the speed of the body or
ii) by keeping the speed constant but by changing the direction.
5. Velocity is measured in
i) cm/s (cm s-1
) in cgs system of units
ii) m/s (m s-1
) in SI system of units and
iii) km/h (km.p.h., km h-1
) in practical life when
distance and time involved are large.
Home Next Previous

23. Average Velocity
When a body moves with variable velocity, the average velocity of the body is
the ratio of the total (net) displacement covered by it to the total time taken.
Average velocity =
Net displacement
Total time taken
or
vav =
stot
ttot
For a body moving with uniform acceleration, vav =
2
u + v
Average velocity is also defined as the change in position or displacement
(Δx) divided by the time intervals (Δt), in which the displacement occurs:
vav =
x2 – x1
t2 – t1
or vav =
Δx
Δt
Note: No effort or force is required to move the body with uniform velocity.
Uniform Velocity
A particle or a body is said to be moving with uniform velocity, if it covers
equal displacements in equal intervals of time, howsoever small these
intervals may be.
Variable Velocity
A particle or a body is said to be moving with variable velocity, if its speed or
its direction or both changes with time.
Home Next Previous

24. a) If a particle undergoes a displacement s1 along a straight line in time t1
and a displacement s2 in time t2 in the same direction, then
b) If a particle undergoes a displacement s1 along a straight line with velocity
v1 and a displacement s2 with velocity v2 in the same direction, then
c) If a particle travels first half of the displacement along a straight line with
velocity v1 and the next half of the displacement with velocity v2 in the same
direction, then
d) If a particle travels for a time t1 with velocity v1 and for a time t2 with
velocity v2 in the same direction, then
e) If a particle travels first half of the time with velocity v1 and the next half
of the time with velocity v2 in the same direction, then
vav =
s1 + s2
t1 + t2
vav =
(s1+s2) v1 v2
s1v2 + s2 v1
vav =
2 v1 v2
v1 + v2
vav =
V1t2 + v2 t2
t1 + t2
vav =
v1 + v2
2
(in the case (b) put s1 = s2)
(in the case (d) put t1 = t2)
Home Next Previous

25. Posit
ion
x
(m)
Time t (s)
O
Posit
ion
x
(m)
Time t (s)
O
Posit
ion
x
(m)
Time t (s)
O
x – t graph for
stationary object
x – t graph for an
object with +ve velocity
x – t graph for an
object with -ve velocity
Posit
ion
x
(m)
Time t (s)
O
The slope of P1P2 gives
average velocity.
x1
t2
x2
t1
P1
P2
Average Velocity
Uniform Velocity
Home Next Previous

26. Difference between Speed and Velocity
Speed Velocity
1. Speed is the time rate of change of
distance of a body.
1. Velocity is the time rate of
change of displacement of a body.
2. Speed tells nothing about the
direction of motion of the body.
2. Velocity tells the direction of
motion of the body.
4. Speed of the body can be
positive or zero.
4. Velocity of the body can be
positive, zero or negative.
3. Speed is a scalar quantity. 3. Velocity is a vector quantity.
5. Average speed of a moving
body can never be zero.
5. Average velocity of a moving
body can be zero.
Home Next Previous

27. Instantaneous Velocity
When a body is moving with variable velocity, the velocity of the body at any
instant is called instantaneous velocity.
The velocity at an instant is defined as the
limit of the average velocity as the time
interval Δt becomes infinitesimally small.
Suppose we want to calculate the
instantaneous velocity at the point P
at an instant t.
Positio
n
x
(m)
Time t (s)
O
x1
t4
x2
t3
P3
P4
P1
P2
t t2
t1
x4
x3
P
The slope of P1P2 at t1 and t2 with intervals
of Δt from t, (i.e. t1 = t- Δt and t2 = t+ Δt)
gives the average velocity at P.
The slope of P3P4 at t3 and t4 with intervals of Δt/2 from t, (i.e. t3 = t- Δt/2 and
t4 = t+Δt/2) gives the average velocity at P which is the closer value to the
instantaneous velocity.
Proceeding this way, Δt may be gradually reduced to approach zero,
i.e. Δt → 0 to get the actual value of the instantaneous velocity.
Though average speed over a finite interval of time is greater than or equal to
the magnitude of the average velocity, instantaneous speed at an instant is
equal to the magnitude of the instantaneous velocity at that instant. Why so?
v =
Δx
Δt
lim
Δt→0
dx
dt
v =
or
Home Next Previous

28. Uniform Motion in a Straight Line
A body is said to be in uniform motion, if it covers equal displacements in
equal intervals of time, however small these time intervals may be.
Formula for uniform motion
At t=0 At t=t1 At t=t2
O A B C
Suppose the origin of the position axis is point O and the origin for time
measurement is taken as the instant, when object is at point A such that
OA = x0.
If at time t1, the object moving with velocity v is at point B such that OB = x1,
then
x1 = x0 + vt1 ………..(1)
Similarly, if at time t2, the object is at point C such that OC = x2,
then x2 = x0 + vt2 ………..(2)
From equations (1) and (2), x2 – x1 = v(t2 – t1) and
x1
x2
v =
x2 – x1
t2 – t1
x0
Home Next Previous

29. The following points are true for Uniform Motion:
1.Generally, the displacement may or may not be equal to the actual
distance covered by an object. However, when uniform motion takes place
along a straight line in a given direction, the magnitude of the displacement
is equal to the actual distance covered by the object.
2.The velocity of uniform motion is same for different choices of t1 and t2.
3.The velocity of uniform motion is not affected due to the shift of the origin.
4.The positive value of velocity means object is moving towards right of the
origin, while the negative velocity means the motion is towards the left of
the origin.
5.For an object to be in uniform motion, no cause or effort, i.e. no force is
required.
6.The average and instantaneous velocity in a uniform motion are always
equal, as the velocity during uniform motion is same at each point of the
path or at each instant.
Home Next Previous

30. Position - Time Graph: (Uniform motion)
Posit
ion
(
m
)
Time (s)
X2
X1
x0
O t1 t2
B
A
C
Slope of the position-time graph gives the velocity of uniform motion.
v = slope of AB =
BC
AC
v =
x2 – x1
t2 – t1
or
Home Next Previous

31. Velocity -Time Graph: (Uniform motion)
Area under velocity-time graph gives the displacement of the body in
uniform motion.
x2 – x1 = area ABCD = v (t2 – t1 )
v
O
A B
D C
Veloc
ity
(
m/s
)
Time (s)
t1 t2
Home Next Previous

32. NON-UNIFORM MOTION
The particle is said to have non-uniform motion if it covers unequal
displacements in equal intervals of time, however small these time intervals
may be.
Acceleration
If the velocity of a body changes either in magnitude or in direction or both,
then it is said to have acceleration.
For a freely falling body, the velocity changes in magnitude and hence it has
acceleration.
For a body moving round a circular path with a uniform speed, the velocity
changes in direction and hence it has acceleration.
For a projectile, whose trajectory is a parabola, the velocity changes in
magnitude and in direction, and hence it has acceleration.
The acceleration and velocity of a body need not be in the same direction.
Eg.: A body thrown vertically upwards.
Home Next Previous

33. For a body moving with uniform acceleration,
the average velocity is
A body can have zero velocity and non-zero acceleration.
Eg.: For a particle projected vertically up, velocity at the highest point is
zero, but acceleration is -g.
If a body has a uniform speed, it may have acceleration.
Eg.: Uniform circular motion
If a body has uniform velocity, it has no acceleration.
When a body moves with uniform acceleration along a straight line and
has a distance ‘x’ travelled in the nth
second, in the next second it travels
a distance x + a, where ‘a’ is the acceleration.
Acceleration of free fall in vacuum is uniform and is called acceleration
due to gravity (g) and it is equal to 980 cms-2
or 9.8 ms-2
.
vav =
u + v
2
Home Next Previous

34. Acceleration of a particle is defined as the time rate of change of its velocity.
or
The acceleration of a particle at any instant or at any point is called
instantaneous acceleration.
or or
Note:
1. Acceleration is a vector quantity.
2. Direction of acceleration is the same as the direction of velocity of the
body.
3. Acceleration can be either positive, zero or negative.
4. Acceleration of a body is zero when it moves with uniform velocity.
5. Acceleration is measured in
i) cm/s2
(cm s-2
) in cgs system of units
ii) m/s2
(m s-2
) in SI system of units and
iii) km/h2
(km h-2
) in practical life when distance and time involved are
large.
aav =
v2 – v1
t2 – t1
aav =
Δv
Δt
a =
Δv
Δt
lim
Δt→0
dv
dt
a =
d2
s
dt2
a =
Home Next Previous

35. Eg.2:
The motion of a sliding block on a
smooth inclined plane is uniformly
accelerated motion.
Uniform Acceleration
A body has uniform acceleration if its
velocity changes at a uniform rate.
If equal changes of velocity take place
in equal intervals of time, however
small these intervals may be, then the
body is said to be in uniform
acceleration.
or
Eg.1:
The motion of a freely
falling body is
uniformly accelerated
motion.
Home Next Previous

36. Non-uniform Acceleration
A body is said to be moving with non-uniform acceleration, if its velocity
increases by unequal amounts in equal intervals of time.
A body has non-uniform acceleration if its velocity changes at a non-
uniform rate.
or
Eg.:
The motion of a car on a crowded city road. Its speed (velocity) changes
continuously.
Retardation or Deceleration or Negative Acceleration
A body is said to be retarded if its velocity decreases w.r.t. time.
A car is decelerating to come to a halt. Home Next Previous

37. Position - Time Graph
Uniformly decelerated
(Negative acceleration)
Position
x
(m)
Time t (s)
Position
x
(m)
Time t (s)
Uniform motion
(Zero acceleration)
Position
x
(m)
Time t (s)
Uniformly accelerated
(Positive acceleration)
Home Next Previous

38. Velocity - Time Graph (Uniformly accelerated / decelerated)
Ve
loc
ity
(m
/s)
Time (s)
v0
v
O t
Ve
lo
cit
y
(m
/s
)
Time (s)
v0
v
O t
Ve
loc
ity
(m
/s)
Time (s)
-v0
-v
O
t t2
t1
Ve
loc
ity
(m
/s)
Time (s)
v0
-v
O
Motion in positive direction
with positive acceleration
Motion in positive direction
with negative acceleration
Motion in negative direction
with negative acceleration
Motion with negative acceleration.
B/n 0 & t1 in positive x-axis and b/n
t1 & t2 in negative x-axis
Home Next Previous

39. Take time along x-axis and distance along y-axis.
Distance-Time Graph for Uniform Motion

40. Analyse the given data and make a proper choice of scale for time and distance.

41. Plot the points.

42. Join the points.

43. CONSIDER ANY TWO POINTS (A, B) ON THE STRAIGHT LINE GRAPH.

44. DRAW PERPENDICULARS FROM A AND B TO X
AND Y AXES.

45. JOIN A TO C TO GET A RIGHT ANGLED TRIANGLE ACB.
Write the title of the graph.

46. CONSIDER ANOTHER TWO POINTS P AND Q ON THE GRAPH AND
CONSTRUCT A RIGHT-ANGLED TRIANGLE PRQ.

47. DISTANCE-TIME GRAPH FOR NON -
UNIFORM MOTION
• TAKE TIME ALONG X-AXIS AND DISTANCE ALONG Y-AXIS.

48. Analyse the given data and make a proper choice of scale for time and distance.

49. PLOT THE POINTS.

50. Join the points.

51. SPEED - TIME GRAPH-UNIFORM SPEED
• DISTANCE TRAVELED BY THE CAR S = V X T
• BUT 60 KM/H = OC = BREADTH OF THE RECTANGLE
OABC
• 5H = OA = LENGTH OF THE RECTANGLE OABC
• I.E., THE DISTANCE COVERED BY THE CAR = LENGTH X BREADTH
= 300 KM.
• TO CALCULATE THE DISTANCE COVERED BY A MOVING OBJECT
FROM A SPEED-TIME GRAPH WE JUST HAVE TO FIND THE AREA
ENCLOSED BY THE SPEED-TIME GRAPH AND THE TIME AXIS.

52. Velocity-Time Graph
Take time along x-axis and velocity along y-axis.

53. ANALYSE THE GIVEN DATA AND MAKE A PROPER CHOICE OF
SCALE FOR X AND Y AXES.

54. JOIN THE POINTS

56. CONSIDER ANY TWO POINTS A AND B ON THE STRAIGHT-LINE
GRAPH.

57. DRAW PERPENDICULARS FROM A AND B TO X AND Y-AXES.

58. JOIN A TO C, ACB FORMS A RIGHT-ANGLED TRIANGLE.

59. •

60. a) Increasing acceleration
Uniform Acceleration Non-uniform Acceleration

61. •
Non-uniform Retardation Uniform Retardation

62. Zero Acceleration

63. Acknowledgement
1. Physics Part I for Class XI by NCERT
2. Body of the car from net
3. Walking man from the net
]
Home End Previous