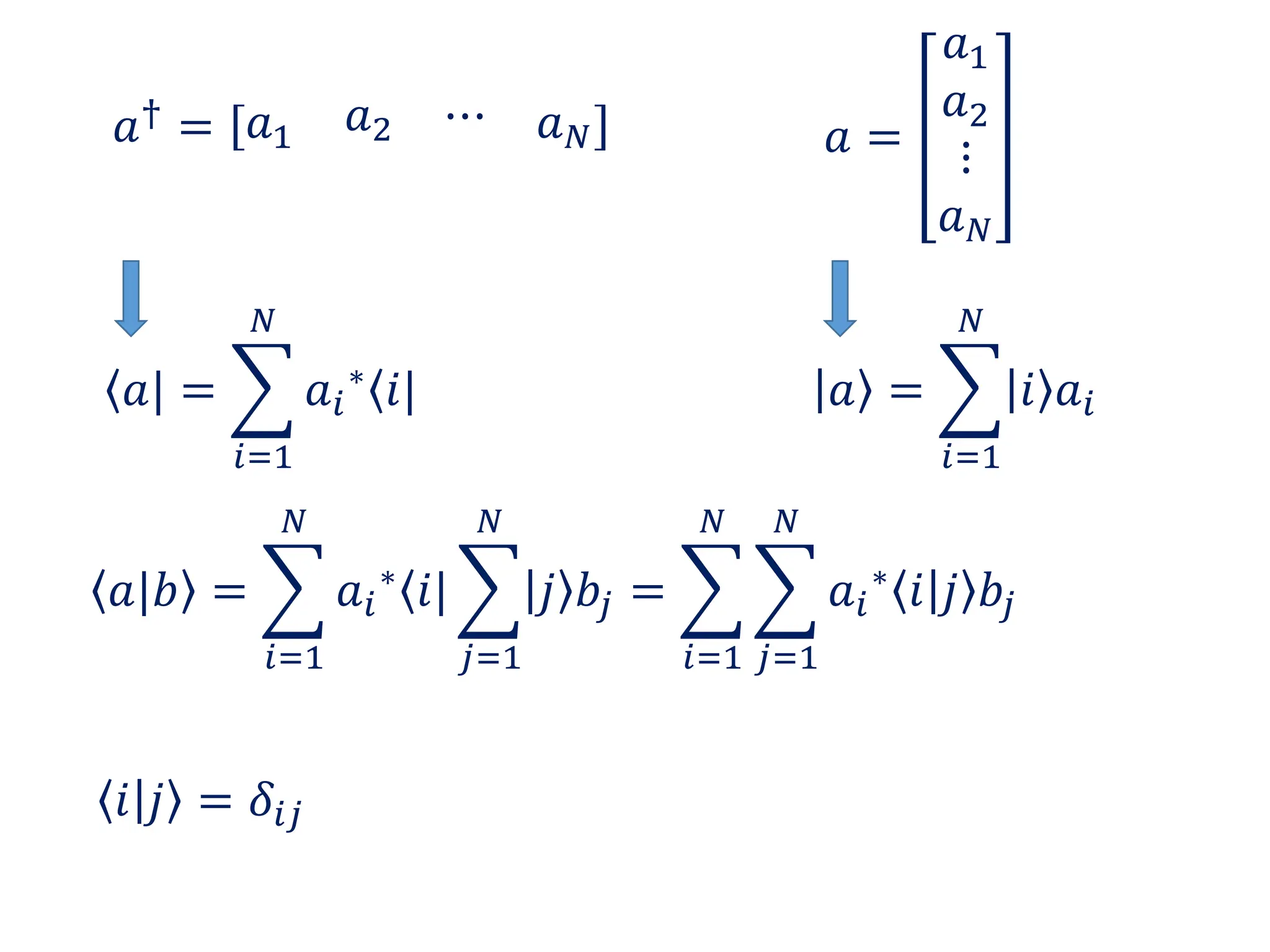This document provides a review of mathematical concepts relevant to physical chemistry, including:
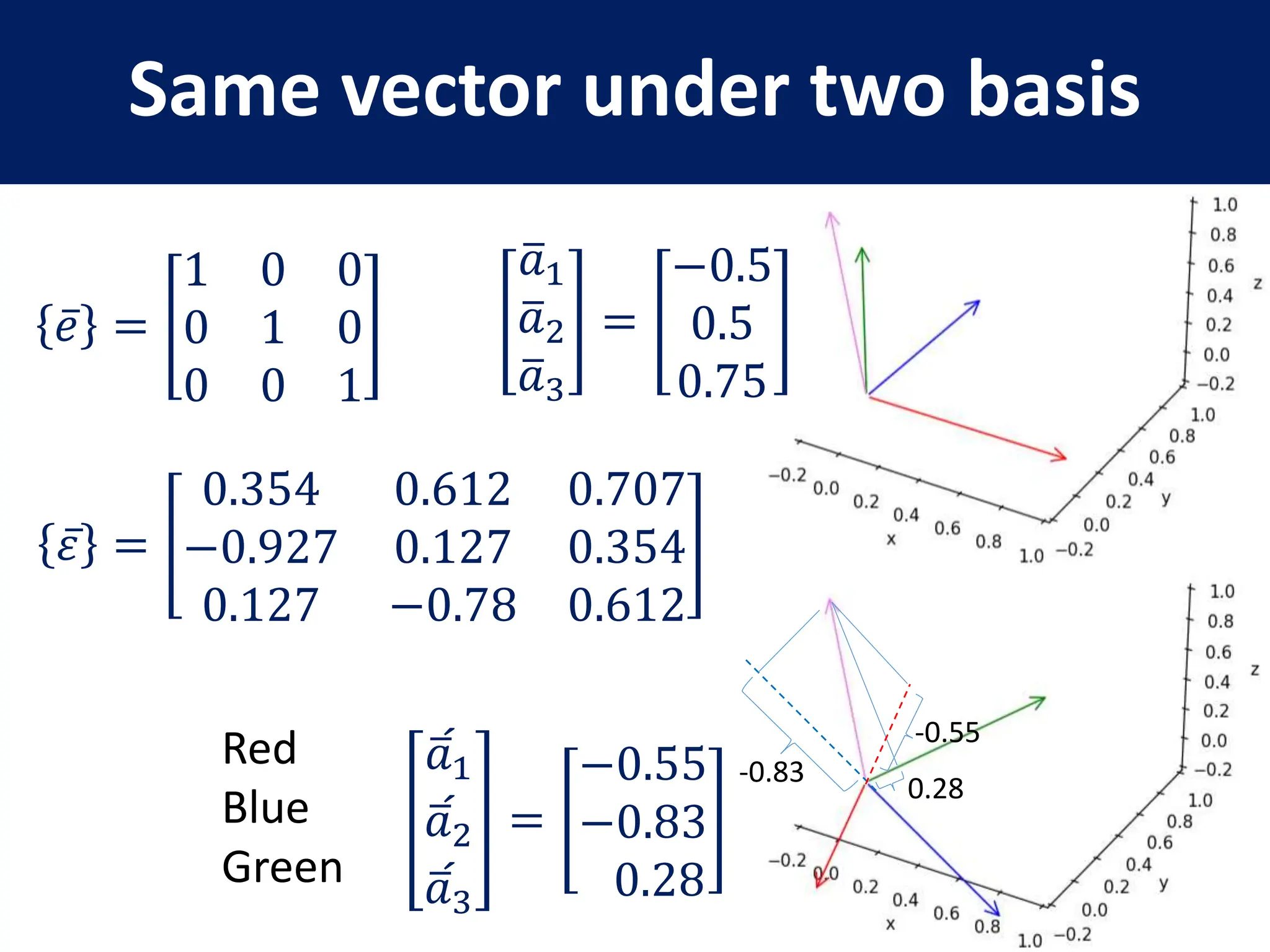
- Representation of 3D vectors in terms of basis vectors and components
- Definition of a basis and examples of standard and non-standard bases
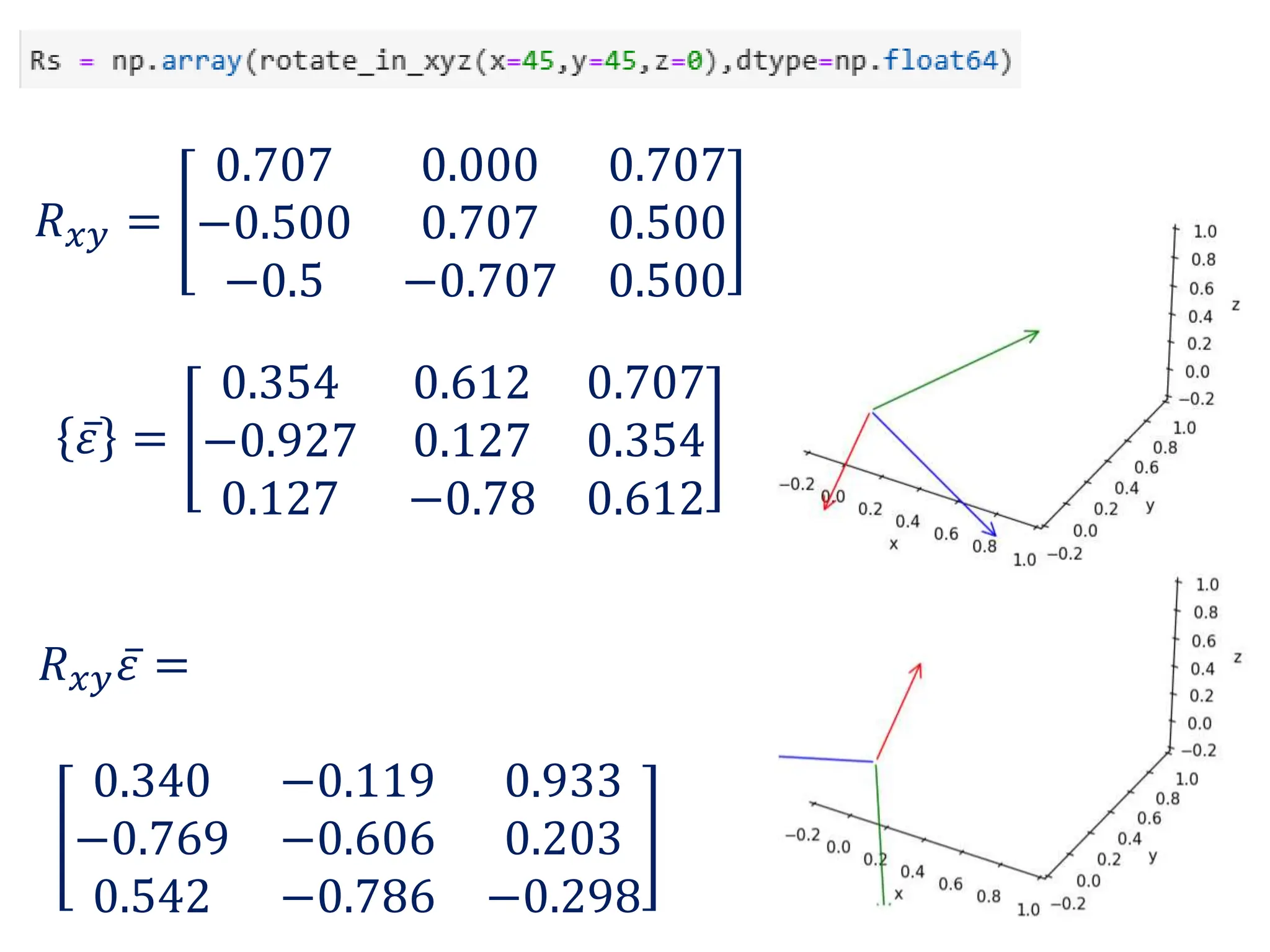
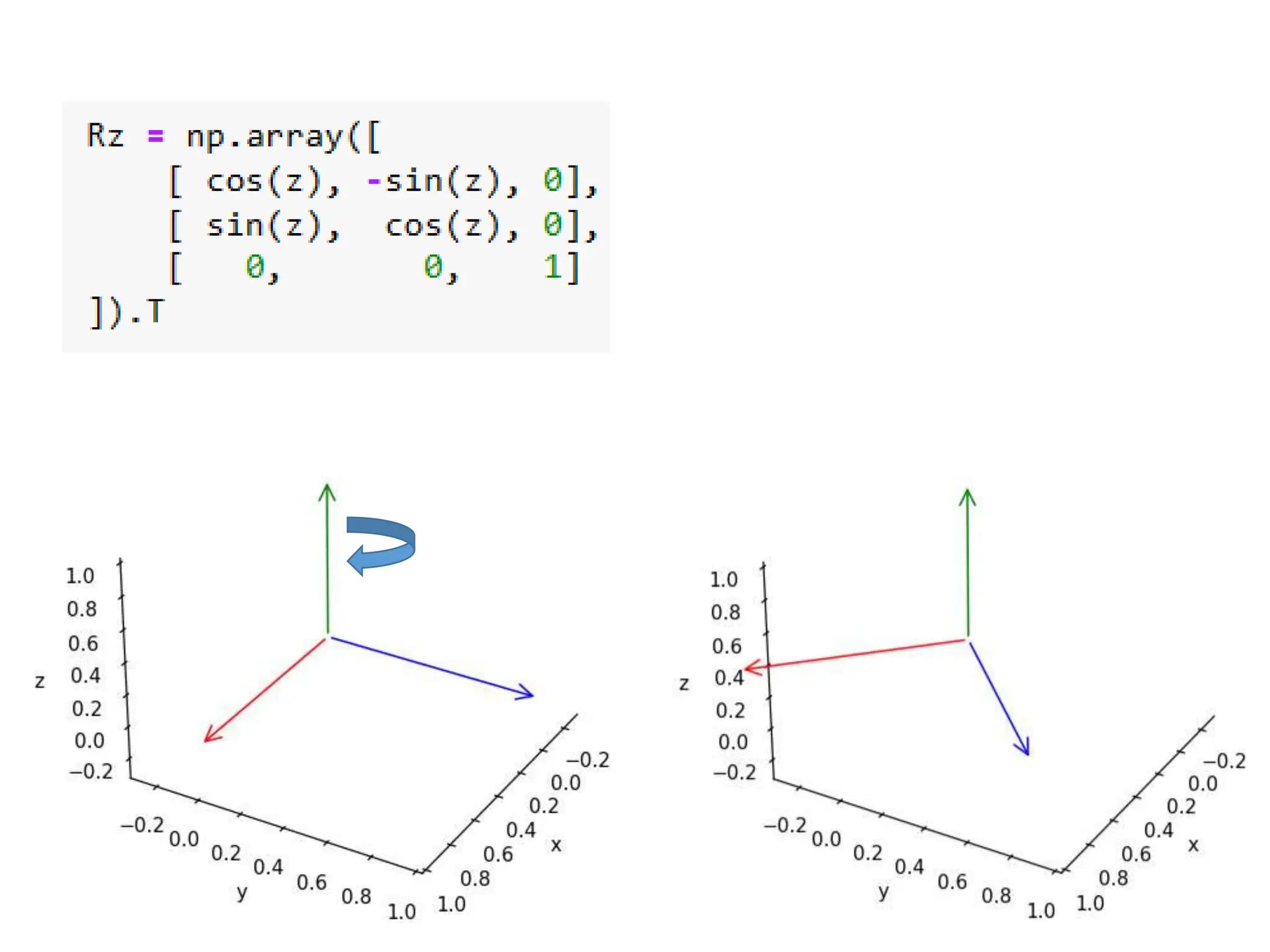
- Representation of vectors and operators in terms of matrices
- Properties of bases, operators, and matrices like orthogonality, linearity, and order of operations
- Key matrix operations like transpose, adjoint, determinant, and representation of vectors and operators